This is the ninth part of a series of blog posts taking a deep look into Ada Lovelace's 1843 computer program, starting with Part 1: First Look at the First Program. A shorter version with less technical background is posted on Ambling along the Aqueduct.

In some of my past posts, I’ve mentioned that Ada Lovelace’s 1843 table from Note G was the first computer program. Now that I’ve gone through the process of getting her program to run as she intended, only on modern hardware, I want to circle back and explain my reasoning.

Whenever talking about “firsts” in innovation, after you’ve narrowed it down to a handful of candidates, which one you pick largely comes down to which precise definitions you are using. Innovation rarely is the result of a single person’s innovation. It’s also rarely a sudden bolt of lightning on a precise day. Instead, it is the result of painstaking work across years, decades, or more, though sometimes moving in fits and starts as pieces come together.

The history of computers and computer programs is no different.

As a life-long programmer, I’ve chosen to write primarily from the point of view of a programmer. That's how I approach this question. It's easy for this question to focus primarily on the hardware and other things extrinsic to the program. Some of that may be unavoidable, but I will try to balance this with a focus on what's intrinsic to the program itself.

That said, while programmers often take hardware for granted, we can’t do anything without the hard work of those that design and build computers, solving innumerable difficult problems, often far outside our areas of knowledge.

Lovelace’s program, of course, wouldn’t have been possible without the virtual machine it was written for, or without the programming language it was written in. These were the in-progress work of Charles Babbage.

Decades before Lovelace began her effort, Babbage had proclaimed in frustration at errors in printed mathematical tables, “I wish to God these calculations had been executed by steam.” In the decades that followed, he had designed first the special purpose Difference Engine, and then in a series of insights, he embarked on the design of the more ambitious general purpose Analytical Engine.

As he worked painstakingly on all of the detailed mechanisms required to do different mathematical operations, he devised and evolved a table-based language to describe the mechanical processes. In the late 1830s, he evolved the table language further to describe the process of what we now call software. He never put all of the ideas together in a single table, but together the ideas he explored independently formed the basis for the programming language Ada Lovelace used in her 1843 table program to calculate the Bernoulli Numbers.

In addition to Lovelace's program, there are a few candidates that might be considered the “first computer program”. I will look at each candidate in turn, but let’s start with some precise definitions.

What is a Computer?

We’re all pretty familiar with what a computer is, but we don’t often think specifically about what makes a given device a “computer.” Before the 1940s, “computer” was a job title for a person who carried out a series of calculations manually. With the introduction of computing machines in the 1940s, the machines were called “electronic computers” to differentiate from the human role. Over the years, as more and more electronic computers were built, the human job was phased out and eventually “electronic” was dropped.

Before settling on an overall definition of computer, let’s look at modern computers, after the rush of innovations of the 1940s and early 1950s.

Since the late 1950s, nearly every computer built has been fundamentally the same in some key ways. When we think of a modern computer, whether it fills a room or fits on your wrist, whether it has hundreds of bytes of RAM or billions, “computer” is shorthand for a programmable, electronic, general-purpose, digital, stored-program computer that is Turing-complete and supports array indexing.

That’s quite a mouthful. Let’s look at each of those criteria.

Programmable just means that you can give the computer one set of instructions and it will carry them out. If you want the computer to do something entirely different, you can give it a different set of instructions and it will carry those out as well. This allows an extreme amount of power and flexibility. There will always be a finite number of possibilities for a program of a given size, but even with just 100 instructions, that number might as well be infinite.

This is obviously of primary importance to a programmer.

Electronic is a low-level hardware detail. Modern computers are built with transistors, but vacuum tubes used to serve the same purpose and are also electronic. Relays are considered electromechanical in that they function similarly but have moving parts driven by electrical signals. Mechanical computers might be powered by electricity, but the internal operation is driven by gears or levels moving physically.

This distinction between mechanical, electro-mechanical, and electronic can have a great impact on the size and speed of a computer, but it doesn’t fundamentally change what it’s like to write a program for it or what programs are possible.

General-purpose means that it’s not limited to solving one kind of problem. It’s related to programmability in that a large enough set of operations are made available and the programmer can choose to arrange them as they see fit.

Digital is in contrast to analog. Values moved around internally might be in binary where bits can be either 1 or 0, or they might be in base-10 where the smallest piece of data can by any digit from 0 to 9, or it can be some other base. But the important thing is that data can only be discrete values, not smoothly varying signals. Digital computers can approximate smoothly varying values using fractional numbers made up of discrete bits or digits, but the data is still fundamentally restricted to discrete values.

All of the devices I'll be looking at are digital.

Stored-program was an innovation from the late 1940s, in the midst of the rapid development of early computers. This distinction is that the machine language instructions that make up a program are themselves data stored in the computer’s memory. A stored-program computer might still use punch cards to input a program, but those are just a means to load the instructions into memory where they are run. This is in contrast with a computer such as Charles Babbage’s design for the Analytical Engine or some computers from the early 1940s where a program was run directly from punched cards or tape.

There are many benefits to a stored-program architecture, but one important one for early computers is that it allows programmers to “cheat” a bit to make up for missing built-in instructions. A simple instruction that can only modify the contents of a single, hard-coded memory location can be modified at run-time to incrementally modify a series of memory locations. This was an early work-around to support array indexing without requiring support for new instructions.

Turing-complete can be thought of as having a powerful enough instruction set to allow it to be equivalent to any other computer. This distinction largely ignores speed and resources. Early computers were very slow and had few resources in modern terms, but a program written for a modern computer could still be adapted to run on an early Turing-complete computer. In practice, what this means is that the computer supports a conditional branch. At runtime, if some condition is found to be true, the computer jumps to one sequence of instructions. If the condition is false, it runs another.

It doesn’t sound like much, but this unlocks a universe of possible programs that are otherwise completely out of reach for a non-Turing-complete computer. From the point of view of a programmer, the vast majority of code I’ve ever written, even trivial bits of code, has used at least one conditional branch and therefore required a Turing-complete computer.

Array indexing is the ability of a computer to operate on a list of values without requiring one separate instruction for each value in the list. For example, a simple program that increases the brightness of an image might just loop over a million pixels and perform a simple addition operation on each in turn. With array indexing, this might be done in a simple loop with just a few instructions, regardless of the size of the image. Without array indexing support of some sort, the computer would require a program of a million instructions to modify a million pixels.

Putting it Together

That defines modern computers. Nearly all devices since the late 1950s that people might think of as a “computer” satisfy all of these parts of the definition: programmable, electronic, general-purpose, digital, stored-program computer that is Turing-complete and supports array indexing.

This definition, though, is too restrictive. It excludes nearly all of the computers from the 1940s, even though from the point of view of a programmer many of them were nearly identical to a modern computer.

A Broader Definition of Computer

Some of these criteria are absolutely essential from the point of view of a programmer. Programmable, of course. General-purpose as well. Digital might not be theoretically essential, but in practice it is tied together with general-purpose, and so is also essential.

From the point of view of a programmer, though, whether or not a computer is electronic doesn’t fundamentally change things. The same is true for stored-program or not. Array indexing support matters quite a bit, as some programs can become unwieldy without it, but it doesn’t make those programs impossible.

Turing-completeness is more important. Running the vast majority of programs on a non-Turing-complete computer is literally impossible, not just unwieldy.

My definition of a computer therefore requires that it be programmable, general-purpose, digital, and also Turing-complete. As we’ll see, this includes some early, pre-modern machines, but excludes others.

What, Then, is a Computer Program?

Once we’ve defined a computer, we can use that as a basis for our definition of a computer program. It’s a series of instructions meant to be run on such a computer.

To be more precise, it might be in the form of raw machine language, or it might be in some higher-level programming language. It might be stored in memory, about to run, or it might simply be handwritten on paper, or maybe it is stored on disk or some other media like punched cards. In an earlier post, I dug into the details of what it means to run a program.

The important thing is that it is recorded in some form readable by a human or a computer, and that it is runnable, that it can be loaded and run in a straightforward way.

There’s a problem, though, with this definition. “Meant to be run” is less an intrinsic quality of the program and more something extrinsic, in the mind of the author, or even whoever happens to be holding a sheet of paper with a program written on it.

It turns out this distinction doesn't change things for the candidate "first computer programs" I'll be looking at, but I think it's important to make the distinction nonetheless.

“Trivial” vs “Complex” Programs

As an example that highlights this problem of intent vs intrinsic qualities of a program, let's look at the simplest runnable program.

Many modern computers have a “NOP” instruction, short for “no operation.” And it does exactly that—nothing. The most trivial program possible would be a sheet of paper with “NOP” written on it. By the above definition, this counts as a computer program. I could run it on a Windows laptop, an Apple watch, and countless other modern computers, not to mention computers from decades ago.

Intuitively, it seems like this should be considered too trivial to count, but where do you draw the line?

Worse yet, imagine I was thinking of my Windows laptop when I wrote NOP on a sheet of paper, but then I handed it to my friend, thinking he might run it on his MacBook. But, really, he plans to run it on his NOP-machine, a special-purpose device he built that is much like a modern computer except that it only supports NOP instructions. It is the opposite of Turing-complete, so it is not a computer by my definition.

Now, this sheet of paper with NOP on it may or may not be a computer program, based solely on who is holding the paper and what they are currently thinking. That seems wrong.

Can we shift the focus back on the program itself? It turns out that it doesn’t take much for a computer to be Turing-complete. Here’s the full instruction set for the 1948 Manchester Baby, one of the earliest computers and also one of the simplest, yet still Turing-complete:

• JMP S - absolute unconditional indirect jump (to location specified in memory S)

• JRP S - relative unconditional jump

• LDN S - load memory into accumulator and negate

• STO S - store accumulator to memory

• SUB S - subtract memory from accumulator

• CMP - skip next instruction if accumulator is negative

• STP - stop

This is simple enough that it should make some sense even if you don't have experience with assembly language. It might seem strange thought that there is no ADD instruction to complement SUB. Can you really do all of arithmetic on this machine?

Yes. The designers realized that they could simplify the hardware at the expense of more complicated programs by leaving out addition, multiplication, and division. A programmer could accomplish addition by using subtraction and the special “load and negate” instruction. Multiplication and division are trickier, but also can be built up from simpler instructions.

Like my NOP example, a program that consists entirely of STP is too trivial to be taken seriously. On the other hand, a program that is six instructions long, consisting only single uses of LDN, SUB, CMP, JMP, STO, and STP can only be run on a Turing-complete computer. The program itself intrinsically requires a Turing-complete computer.

For example, here's a simple program using just those instructions. Some value n is loaded into memory location 6 at the start. After running, if n was negative, the result stored in 8 will be some negative value less than or equal to -2. If n was zero or positive, then the result stored in 8 will be exactly -1.

0: LDN 6
1: SUB 7
2: CMP
3: JMP 1
4: STO 8
5: STP

6: n
7: 1
8: 0

You can tell by looking at the program that it reads and writes data to memory, does some math, and has a conditional branch. That's enough to tell you that this program, even though very simple, intrinsically requires a Turing-complete computer and therefore meets the bar for "complex."

In contrast, here's another program. At first glance, it looks more complicated, but notice there's no CMP or JMP, so there is no conditional branch:

00: LDN 14
01: STO 14
02: LDN 14
03: SUB 15
04: STO 18
05: LDN 18
06: STO 18
07: LDN 16
08: STO 16
09: LDN 16
10: SUB 17
11: SUB 18
12: STO 19
13: STP
14: a
15: b
16: c
17: d
18: 0
19: 0

This program takes the values a, b, c, and d as input, performs the calculation, (a-b)+(c-d), and stores the result in memory location 19. It's made a bit more complicated by the fact that there's no instruction to load a value into the accumulator without negating, and no ADD instruction. Without a conditional branch, though, no matter what input values you give it, the execution flow will be the identical linear sequence. This program intrinsically does not require a Turing-complete computer. You could run this on a simplified version of the Manchester Baby and you'd get the same result. Therefore it fails to meet the bar.

This leads to a crisp, concrete dividing line between “trivial” and “complex” programs. Look at the set of operations used in a program. If that set of operations is enough to require a Turing-complete computer, then it counts as a computer program, intrinsically. If the set of operations used is not Turing-complete, then it is too trivial and does not count as a “computer program.”

My Definition of a Computer Program

Putting it all together, my definition of a computer program is:

A series of instructions to be run on a computer that is programmable, general-purpose, digital, and also Turing-complete. Together the set of instructions used is enough to require that the computer be Turing-complete.

Notably, my definition does not require that the computer yet exist and does not require that the program be run.

While this is my preferred definition, it doesn't makes sense to say that one definition is “correct” and others are simply “wrong.” Broader or more narrow definitions can reasonably be used, if justified and not just asserted or assumed.

When thinking about what was the “first computer program,” the answer depends on your definitions. Most definitions are about the same as mine, above, differing only on the question of whether it must be run to count and whether Turing-completeness is strictly necessary.

As we’ll see, these four different, reasonable definitions give you four different firsts. Additionally, I’ll look at several more candidates, each notable in their own right.

20th Century: If A Program Must Be Run

Talk to any programmer, and they will tell you that their code rarely works perfectly on the first try. Unless it was trivial or they were exceedingly careful, something always goes wrong and something needs to be fixed.

At the same time, a program that is runnable with possibly some minor bugs is still a computer program even before it has been run. “Is it runnable?” is intrinsic to the program, while “has it been run?” is extrinsic.

That said, if you are looking for the first program that has been successfully run, then you must look to the decade from 1938 to 1948. This was a period of rapid innovation, marked by both intense competition and collaboration. Several machines were built with a wide range of capabilities, and those capabilities changed as each team learned from their experience and the experiences of others.

1938 - 1941: Zuse’s Z1 and Z3

Before the famous computers built in the U.S. and U.K., a little known German inventor, Konrad Zuse, built the Z1 in his parent’s home in 1938. The Z1 ran programs from a punched tape made from celluloid film. It was driven by an electric motor, but fully mechanical, capable of performing 22-bit floating point addition and subtraction.

Photograph of Z1 Replica by Mike Peel (www.mikepeel.net)

Mechanical stresses and problems with synchronization meant that it couldn’t run reliably for more than a few minutes. It’s not clear what programs were attempted, but presumably, Zuse was able to successfully run some short test programs despite the unreliability.

In 1941, Zuse completed the Z3, an electromechanical version of the Z1 using about 2600 relays. The use of relays improved the reliability to the point that it is considered by some to be the first working programmable, fully automatic digital computer.

Neither the Z1 nor the Z3 had conditional branches or equivalent functionality, so they were not Turing-complete.

There is a bit of confusion on this point because of a 1997 paper that proved the Z3 was theoretically Turing-complete, just not in a practical sense. The author remarked that “the approach discussed in this paper produces a terrible slowdown of the computation. From a purely theoretical point of view this is irrelevant. From a practical point of view it is clearly the case that nobody would program the Z3 in this way.”

Both the Z1 and Z3 were destroyed in Allied bombing of Berlin in 1943. Zuse built a follow-up, Z4, in 1945, but this also lacked support for conditional branches until it was added in 1950.

Early test programs for the Z1 in 1938 or Z3 in 1941 could be considered the first computer program if one’s definition requires that a program be run, but does not require Turing-completeness.

Between 1942 and 1945, Zuse invented what is thought of as the first high-level programming language, Plankalkül. He didn’t make a compiler or have a way to run his programs, but the language itself was Turing-complete, supporting conditional branches and loops. He wrote some programs in the language, including one for playing chess. These could be considered the first programs in a high-level language, if one doesn’t require that they be run.

1944 - 1946: Harvard Mark I, aka IBM Automatic Sequence Controlled Calculator

In 1944, Howard Aiken at Harvard worked with IBM to create a machine called the Harvard Mark I, or alternatively the IBM Automatic Sequence Controlled Calculator (ASCC). The differing names are one sign of the contentious relationship between Harvard and IBM.

Photo of Harvard Mark I / IBM ASCC

The IBM name is very straightforward and could even be used as a general term for this class of computer. Like Zuse’s Z3, it was programmed with a punched tape (not stored-program) and the machine was not initially Turing-complete. Not having support for conditional branches, it can be thought of as a calculator able to carry out a sequence of computations automatically. Howard Aiken was open about being inspired in his design by reading about Charles Babbage’s Analytical Engine design from a century earlier.

The first programs run on the machine would have been test programs at IBM in 1943 right before it was delivered to Harvard, having been proven to be operational. As these were two years later than Zuse’s Z3, they would not be considered the first by any definition.

In 1945, Grace Hopper published "Tables of the Modified Hankel Functions of Order One-Third and of Their Derivatives" which appears to be the first published results of running a computer program–though still on a non-Turing-complete computer.

Later, in 1946, the machine was upgraded to support conditional branching. At this point, it was the second computer, after ENIAC, to become Turing-complete. One might say that, again, it missed out on being the first to run a Turing-complete program. There is some room for arguing significance, though, as the ENIAC required a cumbersome, days-long rewiring process that was considered part of the “program” while the Harvard machine required simply swapping in a new tape.

1945 - 1948: ENIAC

In 1945, ENIAC became operational. This was the first programmable, electronic, general-purpose digital computer. Notably it was the first Turing-complete computer, as it had conditional branches. Also notable was the speed–it could perform 5,000 additions or over 300 multiplications in a second, much faster than Harvard’s 3 additions per second or 1 multiplication every 6 seconds. That's the power of being an electronic computer using vacuum tubes vs Harvard’s electromechanical, relay-based hardware.

Photograph of Glenn Beck and Betty Snyder Programming the ENIAC

From a programming perspective, the speed was nice, but being Turing-complete was a game-changer. It meant that the universe of possible programs and problems that could be solved became much greater.

On the downside, a program for the original ENIAC configuration included a complex wiring diagram, and “loading” the program meant a days-long effort of connecting wires between the various hardware components.

When ENIAC became operational, the first serious program run was a classified simulation for the development of hydrogen bombs, started in December 1945. Earlier, test programs had been run, including an example calculating a table of squares, published in “Description of the ENIAC and Comments on Electronic Digital Computing Machines” https://apps.dtic.mil/sti/citations/AD0498867

If one’s definition of the first computer program is that it must have been run on a Turing-complete computer, then one of these test programs would be the first.

Later, ENIAC was converted to “stored-program” architecture, and in April 1948, Adele Goldstein is credited with developing and running the first stored program.

1948: Manchester Baby

In contrast to the ENIAC which weighed 27 tons, the Manchester Baby was much smaller, weighing in at only 1 ton. The design was a simple stored-program computer from the start, supporting the limited set of seven possible instructions mentioned above.

Photograph of Manchester Baby Replica

The first program run was a simple test to find the largest factor of a large power of two. After 52 minutes, it reported the expected answer. While this program was run in June of 1948, two months after ENIAC’s first stored-program run, there was some controversy. ENIAC’s implementation of a stored program repurposed a module that had been used for manually entering constants used in computation, and program instructions couldn’t be modified by the running program itself. Supporters of the Manchester Baby point out that this was not a fully modern stored-program architecture.

While Manchester Baby didn’t directly support array indexing, its fully stored-program architecture meant that a program could read or write to an array using self-modifying code. The program would overwrite instructions to point to incrementing addresses, getting the same effect as native support for array indexing in the instruction set.

If one’s definition of first program requires that a program be run on a Turing-complete stored-program computer, and one does not accept ENIAC as such, then this program would be the first.

Manchester Baby was perhaps the first to fully satisfy the definition of a modern computer that I gave at the start: programmable, electronic, general-purpose, digital, stored-program computer that is Turing-complete and supports array indexing.

After 1948, countless other programs were run on countless other computers, nearly all satisfying this definition of modern computer.

19th Century: If it Doesn’t Need To Be Run

I’ve just talked about several programs run on computers from 1938-1948. Depending on your preferred definitions each might be considered the first computer program to be run.

While it’s true that running and debugging a program is an important part of the process, it's worth recognizing the first runnable programs even if the computer they were intended for was never built. Before 1938, no devices were built that could be considered a computer by even a broad definition, but Charles Babbage designed the Analytical Engine, a mechanical computer in the 19th century. He started in 1834 and culminated in his “Plan 28a” design in the late 1840s.

The Analytical Engine was never built, but his design served as a virtual machine that programs could be written for. There were, in fact, 40 program and program-like tables constructed for the Analytical Engine between 1836 and 1843. All of these are worth a closer look.

1836-1840: Babbage’s Tables

Between 1836 and 1840, Charles Babbage constructed a series of tables, 36 in all. These are often referred to by their archival reference, “Series L,” with files numbering 1-27, with each file containing between one and three tables.

Looking at the two tables in Series L #1, they are clearly runnable on a computer. At the top-right, the initial values for v1 through v6 are given, and on the right side, two unlabeled columns show a series of operations that would be familiar to any programmer.

For example, the first operation is listed as:

v7= v5*v1

It’s pretty clear that the value in v5 is multiplied with the value in v1, and the result is stored in v7. When variables are assigned new values, Babbage signifies this with an increasing number of tick marks by the variable. Transliterating these operations to a modern programming language like C would be trivial. Other columns give additional information, “Number of Operation” is like a modern line number, and much of the rest is the equivalent of modern end of line comments, describing the higher-level meaning of the operation for a human reader.

When you look through the rest of the tables, they all take a similar form, but it’s striking that most of the tables omit key details, especially which variables are to be acted upon and which are to receive results. Only 6 of the 36 tables have this variable information, required to run. If you are looking at the tables as programs, then most of these tables are fundamentally incomplete and not runnable.

The first table to contain this variable information is the first table in Series L #1, dated August 4, 1837. It contains seven rows of arithmetic operations. He made note of the number of “great” operations, meaning the more time consuming multiplication and division, as 5, and the number of “small” operations, meaning the much faster addition and subtraction, as 2.

There are no conditional branching operations or other control flow operations, just arithmetic operations. As such, the set of instructions used does not require a Turing-complete computer. This is as one might expect given that his Plan 25, published on August 6, 1840 did not yet have conditional branching, and so wasn’t Turing-complete.

“Given that the 1840 version was incapable of user-programmable conditional branching, the machine described in Plan 25 should be regarded technically as a calculator rather than a computer in the modern sense.” -- Plan 28 Blog

If one’s definition does not require that a program be first run, and does not require that it be for a Turing-complete computer, then the seven instruction table in Series L #1 would be the first program.

The next of Babbage’s tables worth considering is Series L #23, dated June 7, 1838. This is especially interesting. It does not show which variables are used, so it is not runnable, but it has a feature not found in any of the other tables, a precise notation for conditional branching.

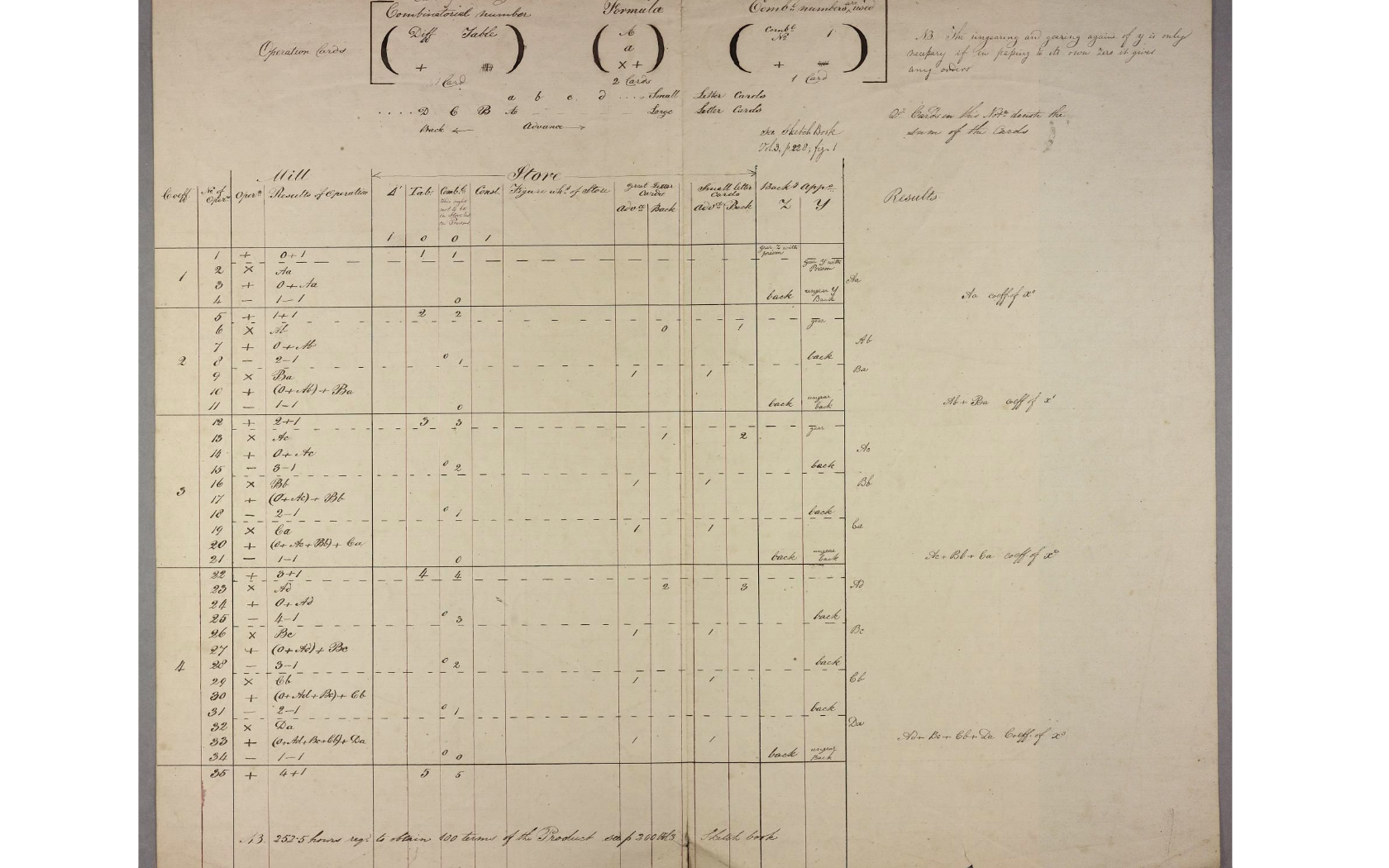
A clue to why Babbage would make this table and leave off the variables is a note at the bottom, “252.5 hours req. To obtain 100 terms of the Product.” This suggests that his goal was to prove the usefulness of conditional branching and to estimate the required time to perform the full calculation. Estimating runtime of a calculation involving conditional branches and loops is non-trivial, and it is easy to see why a sketch of the program would be useful. For this purpose, the actual variables used would be an irrelevant detail, so it makes sense that he omitted them.

As this table omits variables and is therefore not runnable, it would not count as the first program by any definition. At the same time, it is a fascinating milestone. It is the first documentation of a key feature for a Turing-complete computer, over a century before the first Turing-complete computer was constructed.

Looking at the remaining tables in Series L, only #27 is dated earlier than #1, and it does not contain any operations at all. It is an example of how one might specify input variables for a calculation. While not a program, it is a valuable piece of the programming language later used by Lovelace.

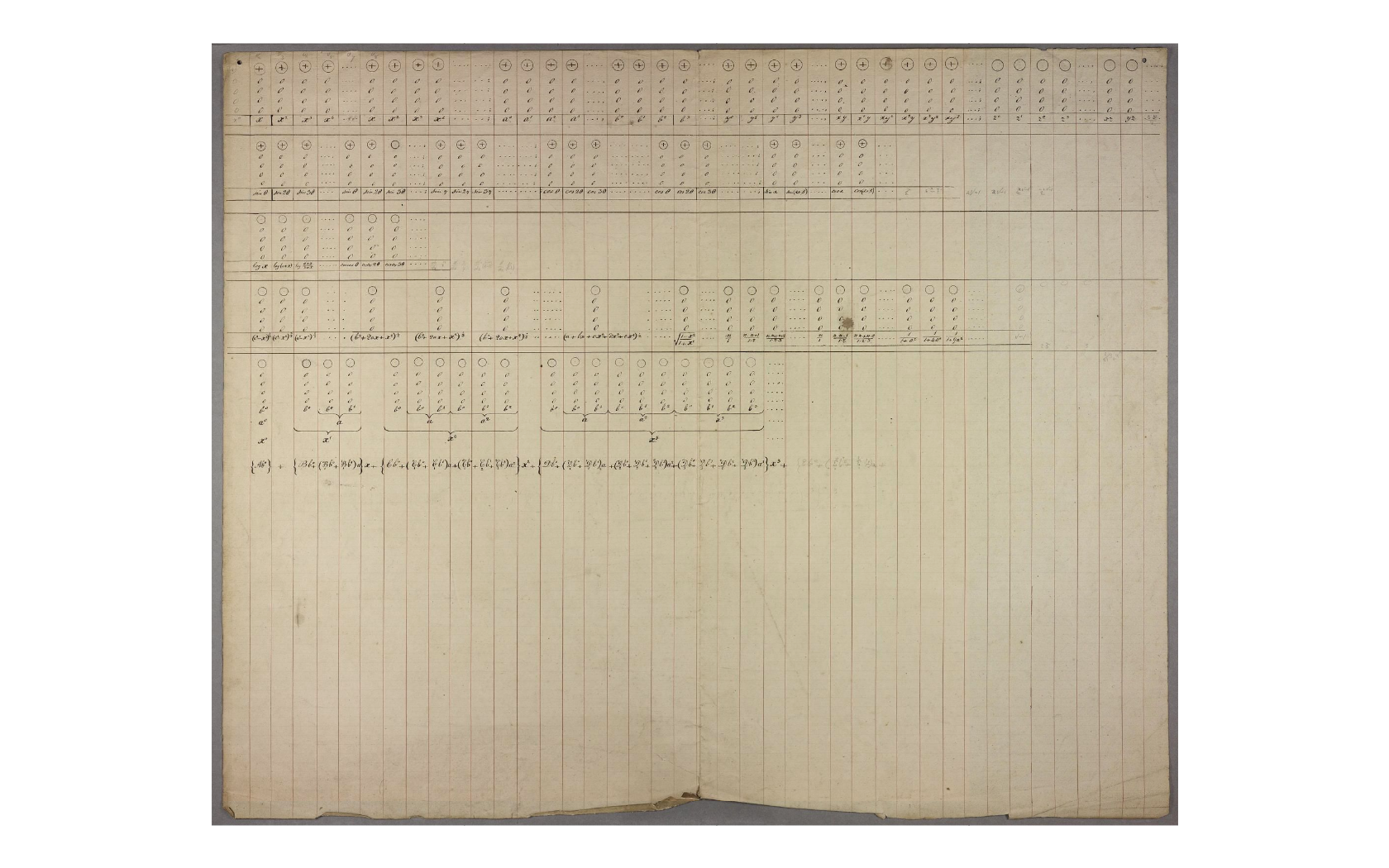
As there are no runnable, Turing-complete tables after #1 in Series L, #1 is the only table that might be considered the first computer program.

1842: Luigi Federico Menabrea’s Tables

After Babbage’s tables, there are just four more to consider. The first of these are the three tables published by Menabrea in 1842 (and later republished in Lovelace's translation). Charles Babbage visited Turin in 1840 and brought along a copy of his Plan 25. Menabrea’s article described the workings of the Analytical Engine and included three tables as examples.

These tables are of the same character as Babbage’s–designed for the non-Turing-complete Plan 25 version of the Analytical Engine. The first is clearly a slightly modified version of Babbage’s Series L #1, with the same seven operations, just variables rearranged to avoid reuse, perhaps in the interests of readability.

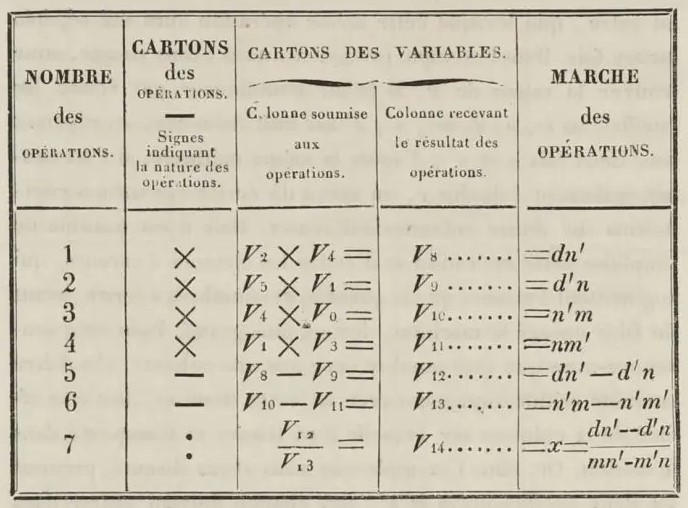
As none of these tables are for a Turing-complete computer, and all were written after Babbage’s #1, none of them can be the first computer program by any definition. At the same time, Menabrea’s 1842 tables (derived from Babbage’s) are the first example of published programs for a non-Turing-complete computer.

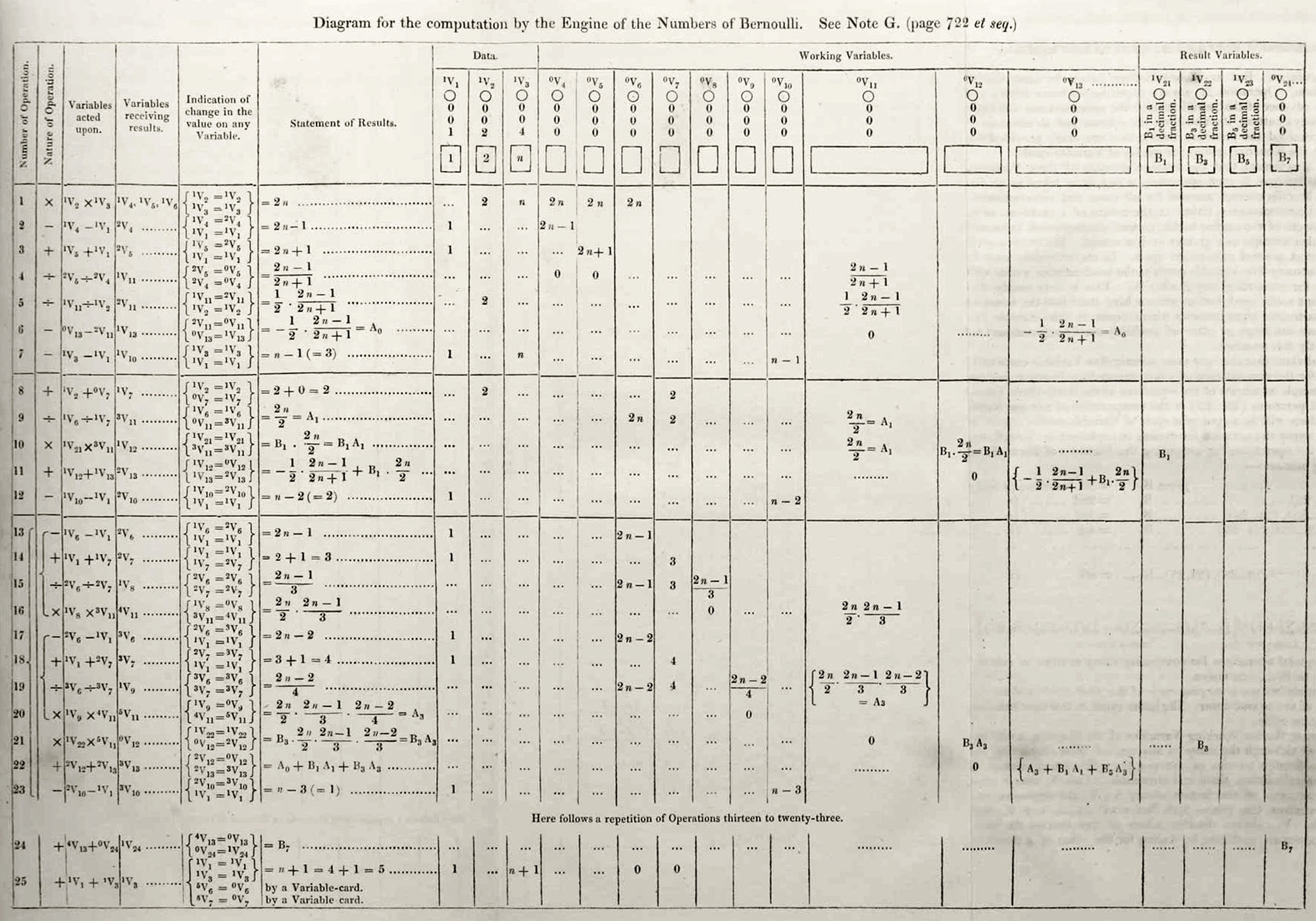
1843: Ada Lovelace’s Note G Table

After Menabrea’s article on the Analytical Engine was published in French, Ada Lovelace was asked to translate the article into English to make it accessible to a local, British audience. This translation was published in 1843. In addition to her translation, Lovelace included a series of “Notes” that far exceeded the original translation in both length and scope. This was a bit of subterfuge to allow her, as a woman, to publish her own thoughts on the Analytical Engine.

In addition to her additional commentary on the Analytical Engine itself and her visionary thoughts about the potentials of what we’d now call software and computer science, she also included an example program in table form that went beyond both Babbage’s and Menabrea’s tables.

The First Programming Language

After seeing Lovelace’s Note G table, Babbage’s Series L tables can be seen in a new light. Together, they document the evolution of a programming language. He started by inventing the table language as means to document the hardware processes of the mechanisms of the Analytical Engine itself. When he started to document sequences of operations that might be fed to the engine as cards, he adapted the table language from a hardware process language to a software programming language.

Following his tables through time, you can see isolated features being investigated:

• 1836 - Series L #27: shows a notation for giving input variables needed for a computation

• August 4, 1837 - Series L #1: uses numbered per-operation rows with columns for the operation number, the type of operation, the variables used in the operation, the variable receiving the operation, a more human-readable statement of results, and a trace table to make it easier to see the progression of the calculation

• June 1838 - Series L #16: a rough notation for a loop, “Repetition of the Same Process,” though without indicating the start operation number to jump to

• June 1838 - Series L #23: horizontal lines marking conditional branches

Lovelace’s 1843 table combines all of these notations together for the first time in one table. Her loop notation adds an indication of the operation to jump to, and she also makes use of a condition variable before both the “repetition” notation and the horizon lines marking conditional branches.

Babbage didn’t add conditional branches to the Analytical Engine design until his 1844 Plan 28, when he wrote down an instruction set that included what he referred to as the “minor operations”:

• Ascertaining if a Variable is Zero;

• Ascertaining if a Variable is Positive or Negative;

The description of these operations make it clear that meeting the condition would cause the cards to move by some amount, essentially a conditional branch. See “Babbage's Analytical Engine Plans 28 and 28a. The programmer's interface”

Lovelace didn’t have time to wait until he had worked out the exact hardware design. In her complex Bernoulli Number program, she realized that she required these conditional branches, so she wrote her program for a virtual machine that extended beyond Plan 25 to include them. Babbage might not have fully worked out the hardware implementation details, but he would have likely showed her his Series L #23 table that showed the horizontal line notation for conditional branches and assured her it was a reasonable feature to rely on.

If one’s definition does not require that a program be first run, but one does require that it be for a Turing-complete computer, then Ada Lovelace’s 1843 table from Note G is the first computer program.

This is my preferred definition. From the point of view of a programmer, it's a program the moment it is written down or typed in. Running it on a real computer is an important next step and will no doubt make it a better program, but it is not required to make it a program. I have shown in my previous blog posts that Lovelace’s program is runnable with only minor adjustments, something to be expected for any non-trivial program.

Additionally, from the point of view of a programmer, Turing-completeness is important. The universe of programs possible for a non-Turing-complete device is far reduced and fundamentally limited.

Ada Lovelace’s 1843 program is the first runnable program that is also written for a Turing-complete computer. Additionally, the program itself intrinsically requires a Turing-complete computer. This makes it the first computer program by my definition.

Ada Lovelace as the First Programmer

Lovelace first met Babbage at a party in 1833. She was fascinated with his description of the Difference Engine, and their intellectual friendship continued over the years, through her marriage to William King and the birth of her three children. As Babbage began work designing the Analytical Engine, she saw the potential of it and, in 1841, she approached Babbage about dedicating herself to work related to the machine, writing:

I am very anxious to talk to you. I will give you a hint on what. It strikes me that at some future time […] my head may be made by you subservient to some of your purposes & plans. If so, if ever I could be worthy or capable of being used by you, my head will be yours. And it is on this that I wish to speak most seriously to you.

In 1842, when L.F. Menabrea wrote an article in French about the Analytical Engine, this was her opportunity. She translated the article into English and appended her series of “notes”. While Menabrea was primarily concerned with a description of the workings of the machine, Lovelace’s notes added her original ideas about a vision for the machine beyond merely mathematical calculations.

Much has been written about her high-level ideas about computing, but as a programmer, what I found most interesting in her notes was her example program and all of her concrete discussions about the program and the process of creating it.

While her notes contain several mathematical formulas as examples, only the formulas related to the Bernoulli numbers are drawn out to a full, runnable program in the form of a table. In a letter from June 26, 1843, she wrote to Babbage:

I want to put in something about Bernoulli’s Numbers, in one of my Notes, as an example of how an implicit function, may be worked out by the engine, without having been worked out by human head & hands first. Give me the necessary data & formulae.

Decades later, in his autobiography, “Passages from the Life of a Philosopher,” Babbage wrote about Lovelace’s notes:

We discussed together the various illustrations that might be introduced: I suggested several, but the selection was entirely her own. So also was the algebraic working out of the different problems, except, indeed, that relating to the numbers of Bernoulli, which I had offered to do to save Lady Lovelace the trouble. This she sent back to me for an amendment, having detected a grave mistake which I had made in the process.

The notes of the Countess of Lovelace extend to about three times the length of the original memoir. Their author has entered fully into almost all the very difficult and abstract questions connected with the subject.

As she requested, Babbage gave her the algebraic formulae—included in Note G as equations numbered (1)-(9). The first three give alternative math for calculating Bernoulli numbers. The remaining six, (4)-(9) derive an equation that can be used as a starting point for her program. This would be the one “algebraic working out” that Babbage supplied and that Lovelace corrected.

From this math, Lovelace methodically developed her program, the table included with and described in great detail in Note G.

The Algebraic Formulæ

In her discussion of cycles (in modern terms, loops) in Note E, she explains the importance of deriving the “nth function” of a formula. This puts the math in a form that can then be implemented in a loop over n. This is the form of the result of derivation of (8) and (9):

(8.) 0 = -1/2*(2n-1)/(2n+1) + B₁*(2n/2) + B₃*(2n*(2n-1)*(2n-2)/(2*3*4)) + B₅*(2n*(2n-1)...(2n-4)/(2*3*4*5*6)) + ... + B_2n-1

which it may be convenient to write under the general form:

(9.) 0 = A₀ + A₁B₁ + A₃B₃ + A₅B₅ + ... + B_2n-1

The Algorithm

She explains how this math can be used to calculate an arbitrary Bernoulli number in terms of all preceding ones. With the math understood she now lays out the iterative strategy for “computing the Numbers to an indefinite extent, from the very beginning.” This is the algorithm that she then developed as a starting point for writing the program in the table:

On attentively considering (8.), we shall likewise perceive that we may derive from it the numerical value of every Number of Bernoulli in succession, from the very beginning, ad infinitum, by the following series of computations:—

1st Series.—Let n=1, and calculate (8.) for this value of n. The result is B₁.
2nd Series.—Let n=2. Calculate (8.) for this value of n, substituting the value of B₁ just obtained. The result is B₃.
3rd Series.—Let n=3. Calculate (8.) for this value of n, substituting the values of B₁, B₃ before obtained. The result is B₅. And so on, to any extent.

This pseudocode should be somewhat familiar to programmers. It’s not a program in itself, and it isn’t the math. Instead, it is a rough sketch of what the program should do after the math has been adapted.

Define Variables and their Purpose

With the math worked out, and a pseudocode algorithm prepared, she explains in her Notes the other pieces of the process to write the code. In Note D, she divides variables “into three classes”: input “Variables for data”, “Result-Variables” for final results, and “Working-Variables” for transient use between.

In Note G, she also talks about arranging the processes and allocating variables so that “the offices performed by the Variables may be as uniform and fixed as possible.” This structure and organization makes it easier to reason about and troubleshoot the code.

The Table

After receiving and correcting the math from Babbage, creating a pseudocode algorithm from the math, and allocating and organizing variables needed, the next piece was to write the code itself.

For this, she needed a programming language. As I’ve mentioned above, she used the table language that Babbage had experimented with and developed in pieces from 1836 to 1840. She brought all of these pieces together for the first time in her program.

Variables are shown allocated at the top as:

• Data

• Working Variables

• Result Variables

Each row contains a series of columns, these required for computation:

• Number of Operation

• Nature of Operation

• Variables acted upon

• Variables receiving results

• Indication of change in the value on any Variable

Additionally each row has a “Statement of Results” column that serves the role of modern end of line comments, and a per-variable trace to help understand and troubleshoot. Interestingly, she tries to present the trace as much as possible as a “simultaneous view” in terms of n rather than the concrete values one might expect if it was simply a snapshot in time.

And finally, the parts that make the program intrinsically Turing-complete, notation for both forward conditional jumps and backward conditional jumps for loops:

• Horizontal lines, with v10 as a condition variable, for forward jumps

• "Here follows a repetition of Operations thirteen to twenty-three", with v10 as a condition variable, for backward jump

Crunch Time Communication

In the course, of developing the program, Lovelace stayed in constant communication with Babbage. It’s a bit surprising to learn that mail was delivered multiple times a day, giving them something like a modern experience of rapid back and forth communication through email.

Amidst dozens of letters to Babbage, most of the talk is about is about various edits to the text, along with frequent confusion about who had the originals for one section or another. Unlike email, they were unfortunately unable to virtually copy attachments.

Lovelace frequently wrote about her hard work on the program and the problems she encountered. Modern programmers would be familiar with getting bogged down and having to explain missed deadlines. The following letter excerpts are from Ada the Enchantress of Numbers: A Selection from the Letters of Lord Byron's Daughter and Her Description of the First Computer, edited by Betty Alexandra Toole

On being delayed by finding new errors:

I have been hard at work all day, intending to send you the Diagram & all, quite complete. Think of my horror then at just discovering that the Table & Diagram, (over which I have been spending infinite patience & pains) are seriously wrong, in one or two points. […] I shall be up betimes tomorrow morning, & finish off the Table & Diagram; so as to send it [to] you by post;

After completing a new draft:

I have worked incessantly, & most successfully, all day. You will admire the Table & Diagram extremely.

After spending the day getting bogged down and needing to step away from the writing desk to clear one’s mind:

I am in much dismay at having got into so amazing a quagmire and botheration with these Numbers, that I cannot possibly get the thing done today. I have no doubts it will all come out clean enough tomorrow; & I shall send you a parcel up, as early in the day as I can. So do not be uneasy. (Tho’ at this moment I am in a charming state of confusion; but it is that sort of confusion which is of a very bubble nature). I am now going out on horseback. Tant mieux.

As a programmer, I can empathize. Sometimes going off for a walk or a bike ride is exactly what is needed to come back and attack a bug with fresh clarity.

Ada Lovelace's Bug

Despite all of the care she put into the table, it’s not surprising that some bugs persisted. I called attention to two that I had to address to run her program.

The first was a simple transposition of two variables: v5 / v4 when it should have been v4 / v5. It’s impossible to be sure, but given how simple of an error it is and how much trouble Lovelace complained in letters of errors in proofs, I think this is likely a typo introduced by the publisher. The table was highly complex and it’s likely the person typesetting didn’t really understand the details enough to avoid such problems.

The second is more interesting. Operation 24, as printed, doesn’t negate the Bernoulli number when storing the result in a variable. This negation is absolutely essential, and changing it is more than just changing out a couple symbols in the table. It couldn’t have been a typo at the printers. It was a mistake made by Lovelace, and Babbage missed it when he was reviewing her work.

It was the very sort of mistake programmers make all of the time.

The formula that Babbage gave Lovelace was correct:

(9.) 0 = A₀ + A₁B₁ + A₃B₃ + A₅B₅ + ... + B_2n-1

There was one more step, though, that Babbage omitted. To isolate B_2n-1 you need to subtract it from both sides and negate, resulting in something like this:

B_2n-1 = - (A₀ + A₁B₁ + A₃B₃ + A₅B₅ + ...)

Babbage presumably thought (9) was enough and the negation was implicit.

Lovelace, though, missed the implicit subtraction and negation. In her discussion in Note G, in at least four places in the text, she talks about the culmination of A₀ + A₁B₁ + A₃B₃ + A₅B₅ + ... as the same as B_2n-1 and that one must simply store the result. It’s clear that the bug was introduced in the handoff of the math from Babbage to Lovelace. Before she even started writing the code, she had missed the negation due to this minor oversight. She then went through her programming process, culminating in her program that preserved the oversight.

To be clear, this is a minor bug, of the sort that programmers make all of the time. It is the kind you find quickly the first time you run. That’s how I found it.

I find it fascinating, though, to see this bug and her thought processes from over 180 years ago frozen in the text like an ancient bug caught in amber.

I set out to pair debug this program with Ada Lovelace so that I could learn how it worked. Finding her bug and helping her run her program as she intended collapsed the 180 years that separated us. We were two programmers, sitting at a writing desk, together. It works! Check it in.

In my next blog post, I’ll revisit the adjustments required to run Ada Lovelace’s 1843 program, giving a detailed list along with minor corrections to the trace table that were not required to run.