My hot take on Zero-Knowledge Proofs
 Pranav Bawgikar
Pranav Bawgikar
[20]
ZKPs are one of the most powerful tools cryptographers have ever devised, but unfortunately they are relatively poorly understood. I have been studying ZKPs and their uses and, although I am not an expert in them, I thought I would share what I have learned. With that being said, let's begin.
1.0 Origins of Zero-Knowledge
Zero-Knowledge Proof is a technique for confirming the accuracy of information without disclosing any details about the information or the person who provided the proof. A ZKP can allow someone with a secret to convince another person that they know that secret without revealing that secret. That seems pretty unlikely, right? But what if I tell you there's a way to accomplish this? Zero-Knowledge Proofs come into play right here. Zero-Knowledge Proofs are the cryptographic concepts that allow one party (The Prover) to prove the validity of the data or transactions to another party (The Verifier) without revealing the actual information or transaction amount.
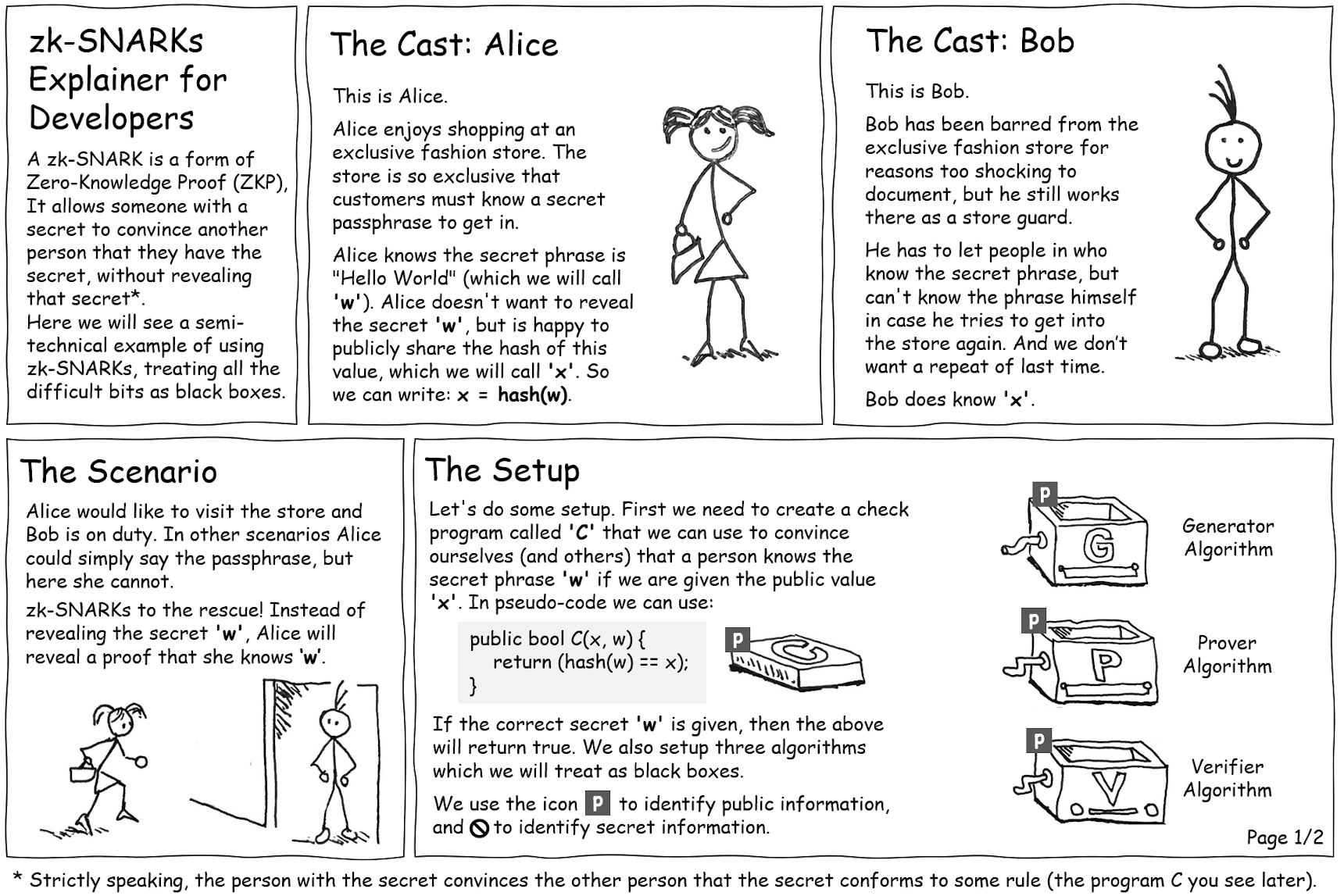
This cartoon illustrated by Kevin Small gives an example of a Zero Knowledge Proof (ZKP) in action. You can check out the full story here.
The notion of ‘Zero Knowledge’ was first proposed in the 1980s by MIT researchers Shafi Goldwasser, Silvio Micali and Charles Rackoff. These researchers were working on problems related to interactive proof systems, theoretical systems where the Prover exchanges messages with the Verifier to convince the Verifier that some mathematical statement is true. The specific concern they raised was information leakage. Concretely, they asked, how much extra information is the Verifier going to learn during the course of this proof, beyond the mere fact that the statement is true?
Let’s see a real-world example: imagine a client wishes to log into a web server using a password. The standard approach to this problem involves storing a hashed version of the password on the server. The login here is sort of a ‘proof’ that a given password’s hash is the output of a hash function that is ran on some ‘password’— and the client actually knows this password. Most real systems implement this ‘proof’ in the absolute worst possible way. The client simply transmits the original password to the server, which re-computes the password hash and compares it with the stored value. The problem here is obvious: the server learns our clear text password*.* Modern password systems are therefore involved with a good deal of praying that these servers aren’t compromised.
Goldwasser, Micali and Rackoff proposed three following properties that every zero-knowledge protocol must satisfy.
Completeness: If a statement is true, then an honest verifier can be convinced by an honest prover that they possess knowledge about the correct input.
Soundness: If a statement is false, then no dishonest prover can unilaterally convince an honest verifier that they possess knowledge about the correct input.
Zero-knowledgeness: If the state is true, then the verifier learns nothing more from the prover other than the statement is true.
2.0 The ZKP Family Tree
Interactive ZKPs
ZKPs that involve many interactions between the prover and the verifier are referred to as interactive ZKPs. The Schnorr protocol and the Fiat-Shamir heuristic are examples of interactive ZKPs. An interactive ZKP session has to deal with multiple back-and-forth communication between the prover and the verifier. Here the verifier tries to validate an input by giving mathematical challenges that only the prover can solve. Until the verifier is persuaded, the verifier challenges the prover.
Non-Interactives ZKPs
With NIZKPs, there is only a one-time communication happening. The prover generates the proof that is sent to the verifier, and the verifier can then checks the proof without any further interaction with the prover. The NIZKPs use the following algorithms:
zk-SNARKs
A zkSNARK (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge) is a gadget that can be used to generate a ZKP for any mathematical function. Basically, you feed the “code” of a function f into a zkSNARK, and the SNARK creates a protocol that allows you to generate zero-knowledge proofs for f. They use a cryptographic method called elliptical curves which makes them gas efficient.
zk-SNARKS are small in size and are easy to verify. In this category of ZKPs, the verifier may only confirm the proof once, at any given time. Compared to interactive ZKPs, this kind of ZKP demands higher processing power.
zk-STARKs
Stands for Zero-Knowledge Scalable Transparent Argument of Knowledge. As opposed to zk-SNARKS, these methods require little interaction between the provider and the verifier. They are also considerably more efficient.
Non-malleable ZKPs
Non-malleable ZKPs provide protection against tampering or manipulation of the proof itself. Even if an attacker tries to modify a valid proof, the modified proof will be rejected.
3.0 Why ZKPs Matter?
Practically, Zero-Knowledge is important because it gives you privacy in situations where you’d otherwise have to reveal confidential information.
Logging into a website: rather than typing your password into a potentially unsafe website, you can simply send a proof that you “know your password”.
Sending private blockchain transactions: rather than sending money on Bitcoin, where your financial ledger is public information, you can send a proof that your money is valid (not double spent) without revealing your balances, as popularized by Zcash.
ZKPs can contribute to scalability by reducing the amount of data that needs to be processed and stored on the blockchain. This is particularly important as Web3 applications aim to handle larger volumes of transactions and computations. ZKPs also allow users to make private transactions where no information regarding the people involved or the amount being sent is displayed. Projects like Zcash and Monero are a good example.
4.0 Zero-Knowledge vs. Zero Trust
The crypto-nerds among you may have heard about Zero Trust as well. Hence, I thought I'd chime in Zero-Trust here to clear some air. Zero-Knowledge really refers to the specific cryptographic method of zero-knowledge proofs, while Zero Trust is a general cyber security model used by organizations to protect their data, premises, and other resources.
The zero-trust framework assumes that every person and device, both internal and external to the network, could be a threat due to malicious behavior or simple incompetence. To mitigate threats, zero-trust systems require users and devices to be authenticated, authorized, and continuously validated before access to resources is granted.
Zero-Knowledge proofs can be used as part of a zero-trust framework. For example, Zero-Knowledge authentication solutions can allow employees to access their organization’s network, without having to reveal personal details.
5.0 Conclusion
ZKPs showcase a significant advancement in cryptography, which enables validating information without revealing any sensitive data. This post was too basic (maybe?) and introductory-ish. In the future, I’ll definitely try to come up with a practical guide to creating ZKPs and implementing them within dApps.
Subscribe to my newsletter
Read articles from Pranav Bawgikar directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Pranav Bawgikar
Pranav Bawgikar
Hiya 👋 I'm Pranav. I'm a recent computer science grad who loves punching keys, napping while coding and lifting weights. This space is a collection of my journey of active learning from blogs, books and papers.