Outliers in Machine Learning: How to Identify, Handle, and Leverage Their Impact

Outliers are data points that deviate significantly from the overall pattern of a dataset. In statistics and data analysis, they are often considered anomalies or rare occurrences that fall far outside the range of typical values. While outliers can sometimes indicate errors in data collection or entry, they can also reveal important insights, such as unusual events or exceptional cases that merit further investigation. Understanding outliers is crucial in fields like finance, healthcare, and engineering, where they can impact the results of analyses and lead to misleading conclusions if not properly handled. Detecting, analyzing, and addressing outliers are therefore essential steps in ensuring data quality and reliability.

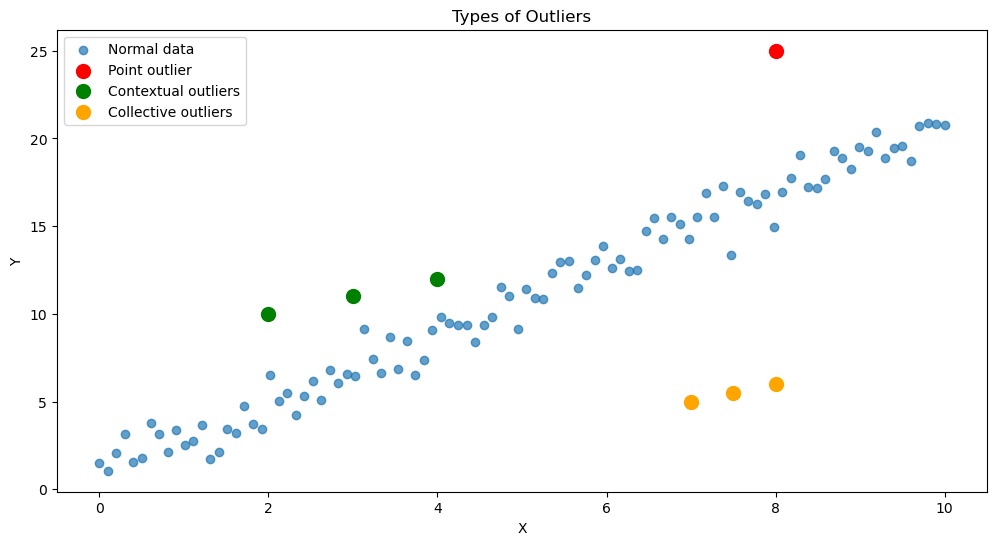
Types of Outliers

Outliers in machine learning can be broadly categorized into three main types: point outliers, contextual outliers, and collective outliers.

1. Point Outliers: These are individual data points that stand out significantly from the rest of the dataset. They differ so much from the majority of the data that they seem disconnected from the overall pattern.

2. Contextual Outliers: These data points appear unusual only within a specific context or under certain conditions. The deviation may not be apparent when looking at the data overall, but it becomes significant when considering the context, such as time or location.

3. Collective Outliers: These are groups of data points that, when taken together, deviate from the expected pattern or structure of the data. Although individual points within the group may not be outliers, the collection as a whole exhibits anomalous behavior.

# Code to visualize various types of outliers as mentioned above

import numpy as np
import matplotlib.pyplot as plt

# Generate data with different types of outliers
np.random.seed(42)
x = np.linspace(0, 10, 100)
y = 2 * x + 1 + np.random.normal(0, 1, 100)

# Add outliers
point_outlier = (8, 25)
contextual_outliers = [(2, 10), (3, 11), (4, 12)]
collective_outliers = [(7, 5), (7.5, 5.5), (8, 6)]

# Plot the data
plt.figure(figsize=(12, 6))
plt.scatter(x, y, alpha=0.7, label="Normal data")
plt.scatter(*point_outlier, color='red', s=100, label="Point outlier")
plt.scatter(*zip(*contextual_outliers), color='green', s=100, label="Contextual outliers")
plt.scatter(*zip(*collective_outliers), color='orange', s=100, label="Collective outliers")

plt.title("Types of Outliers")
plt.xlabel("X")
plt.ylabel("Y")
plt.legend()
plt.show()

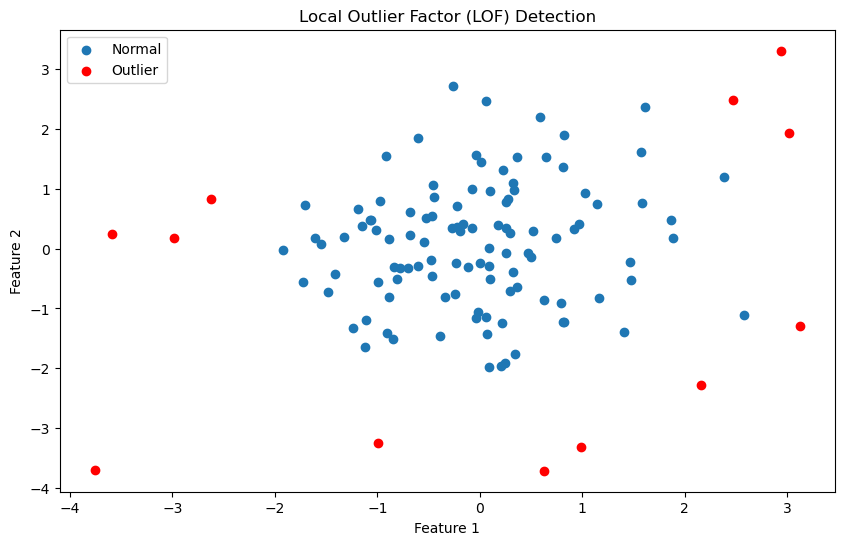
Outlier Detection using Distance-based Method

Distance-based methods for detecting outliers focus on evaluating the distances between data points to spot anomalies. A well-known algorithm in this group is the Local Outlier Factor (LOF), which assesses the local density of a data point relative to the densities of its neighboring points. Points with lower local density compared to their neighbors are given higher LOF scores, indicating a higher likelihood of being outliers.

from sklearn.neighbors import LocalOutlierFactor
import numpy as np
import matplotlib.pyplot as plt

# Generate sample data with outliers
np.random.seed(42)
X = np.random.normal(0, 1, (100, 2))
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.concatenate([X, X_outliers])

# Apply LOF
lof = LocalOutlierFactor(n_neighbors=20, contamination=0.1)
y_pred = lof.fit_predict(X)

# Plot the results
plt.figure(figsize=(10, 6))
plt.scatter(X[y_pred == 1, 0], X[y_pred == 1, 1], label="Normal")
plt.scatter(X[y_pred == -1, 0], X[y_pred == -1, 1], color='red', label="Outlier")
plt.title("Local Outlier Factor (LOF) Detection")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.legend()
plt.show()

print(f"Number of detected outliers: {sum(y_pred == -1)}")

Outliers Handling Methods

In the following major outlier handling methods are discussed.

1) Removal and Transformation

Two common strategies for addressing outliers are removal and transformation. Removal involves discarding the outliers from the dataset, whereas transformation uses mathematical techniques to lessen their impact. Both approaches seek to minimize the effect of outliers on machine learning models.

import numpy as np
from sklearn.preprocessing import RobustScaler

# Generate sample data with outliers
np.random.seed(42)
data = np.random.normal(0, 1, 1000)
outliers = np.array([10, -8, 12, -9, 11])
full_data = np.concatenate([data, outliers])

# Remove outliers
def remove_outliers(data, threshold=3):
    z_scores = np.abs((data - np.mean(data)) / np.std(data))
    return data[z_scores < threshold]

# Transform data using RobustScaler
def transform_data(data):
    scaler = RobustScaler()
    return scaler.fit_transform(data.reshape(-1, 1)).ravel()

# Apply both methods
data_removed = remove_outliers(full_data)
data_transformed = transform_data(full_data)

print(f"Original data range: [{full_data.min():.2f}, {full_data.max():.2f}]")
print(f"Data range after removal: [{data_removed.min():.2f}, {data_removed.max():.2f}]")
print(f"Data range after transformation: [{data_transformed.min():.2f}, {data_transformed.max():.2f}]")

Original data range: [-9.00, 12.00]

Data range after removal: [-3.24, 3.08]

Data range after transformation: [-6.94, 9.20]

2) Capping and Imputation

Capping and imputation are alternative techniques for managing outliers. Capping sets extreme values to a defined limit, while imputation replaces outliers with more typical values. These approaches help preserve the original data size while minimizing the influence of outliers.

import numpy as np
from sklearn.impute import KNNImputer

# Generate sample data with outliers
np.random.seed(42)
data = np.random.normal(0, 1, 1000)
outliers = np.array([10, -8, 12, -9, 11])
full_data = np.concatenate([data, outliers])

# Capping outliers
def cap_outliers(data, lower_percentile=1, upper_percentile=99):
    lower_bound = np.percentile(data, lower_percentile)
    upper_bound = np.percentile(data, upper_percentile)
    return np.clip(data, lower_bound, upper_bound)

# Impute outliers using KNN
def impute_outliers(data, n_neighbors=5):
    imputer = KNNImputer(n_neighbors=n_neighbors)
    return imputer.fit_transform(data.reshape(-1, 1)).ravel()

# Apply both methods
data_capped = cap_outliers(full_data)
data_imputed = impute_outliers(full_data)

print(f"Original data range: [{full_data.min():.2f}, {full_data.max():.2f}]")
print(f"Data range after capping: [{data_capped.min():.2f}, {data_capped.max():.2f}]")
print(f"Data range after imputation: [{data_imputed.min():.2f}, {data_imputed.max():.2f}]")

Original data range: [-9.00, 12.00]

Data range after capping: [-2.20, 2.46]

Data range after imputation: [-9.00, 12.00]

Considerations when Dealing with Outliers

When dealing with outliers in machine learning, several important factors need to be taken into account. Domain expertise is essential for interpreting the context of the data, as it helps to distinguish between true anomalies that need to be addressed and rare events that might hold valuable insights. The size of the dataset also affects how outliers impact the analysis; larger datasets tend to be more resilient to outliers, whereas smaller datasets may be more sensitive to their influence. Furthermore, the choice of machine learning model is critical, as some models—like decision trees and ensemble methods—are naturally more robust to outliers, while others, such as linear regression, can be significantly affected. Lastly, the data's underlying distribution and the presence of skewness should be considered, as they can inform the appropriate methods for managing outliers effectively.

import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression, HuberRegressor
from sklearn.metrics import mean_squared_error

# Generate sample data with outliers
np.random.seed(42)
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = 2 * X.ravel() + 1 + np.random.normal(0, 1, 100)
X_outlier = np.array([[9]])
y_outlier = np.array([25])

X_with_outlier = np.vstack([X, X_outlier])
y_with_outlier = np.hstack([y, y_outlier])

# Train different models
lr = LinearRegression().fit(X_with_outlier, y_with_outlier)
huber = HuberRegressor().fit(X_with_outlier, y_with_outlier)
rf = RandomForestRegressor(n_estimators=100, random_state=42).fit(X_with_outlier, y_with_outlier)

# Evaluate models
models = [lr, huber, rf]
model_names = ["Linear Regression", "Huber Regression", "Random Forest"]

for name, model in zip(model_names, models):
    mse = mean_squared_error(y, model.predict(X))
    print(f"{name} MSE: {mse:.4f}")

Linear Regression MSE: 0.8249

Huber Regression MSE: 0.8164

Random Forest MSE: 0.2071

The Dual Impact of Outliers in Business Machine Learning Applications

Outliers in datasets can significantly impact machine learning models used for business problems, carrying both potential drawbacks and benefits. Understanding these impacts is crucial, as it can guide businesses in handling outliers effectively to either minimize risks or exploit potential opportunities.

Negative Impacts

Outliers often pose challenges by distorting the performance of machine learning models, particularly those sensitive to extreme values, such as linear regression and k-nearest neighbors. These models may become overly influenced by the presence of outliers, leading to poor generalization and inaccurate predictions. For instance, in a sales forecasting model, a few unusually high sales records due to one-time events can cause the model to predict future sales figures that are unrealistically optimistic, resulting in flawed inventory planning or budget allocation. This distortion is especially problematic in smaller datasets where outliers have a more pronounced effect, as they can disproportionately influence model parameters and decision boundaries.

The presence of outliers can also obscure important trends and patterns within the data, making it difficult to derive meaningful insights. When outliers dominate the dataset, statistical measures like mean, variance, or correlation may become biased, leading to misleading interpretations. For example, in customer segmentation analysis, a few extremely high or low spending customers can skew the average spending, making it appear as though the customer base is wealthier or poorer than it truly is. This can result in misguided marketing strategies or inaccurate targeting of customer segments. Furthermore, outliers can increase the error rates of predictive models, thereby reducing overall accuracy and making the models less reliable in making business decisions. This can be particularly damaging in industries like finance or healthcare, where model predictions are used for critical decision-making.

Positive Impacts

While outliers are often viewed as problematic, they can also offer valuable insights and play a positive role in business machine learning applications. In many cases, outliers represent rare but significant events that can reveal hidden opportunities or highlight critical risks. For instance, outliers in transaction data might indicate fraudulent activities, which, if detected early, can help a business prevent financial losses. In industrial applications, outliers in sensor data may point to equipment malfunctions or potential safety hazards, allowing for timely maintenance or interventions before a serious failure occurs.

Outliers can also uncover new business opportunities by highlighting emerging trends or niche customer behaviors that might otherwise go unnoticed. For instance, a surge in online searches for a particular product may appear as an outlier in sales data, indicating growing consumer interest. By identifying and analyzing these outliers, companies can capitalize on trends earlier than competitors, adjusting their product offerings or marketing strategies accordingly. Moreover, the identification of unique customer segments, characterized by distinct purchasing patterns or preferences, can enable businesses to tailor their products or services more effectively to meet specific needs, thereby driving growth in underexplored markets.

Additionally, outliers play an important role in enhancing risk management strategies. They can provide insights into potential vulnerabilities by indicating extreme cases or exceptions that standard models may overlook. For example, during financial market analysis, detecting outliers related to sudden price movements could help investors anticipate and prepare for market crashes. Similarly, in supply chain management, recognizing outliers related to rare but impactful disruptions can assist companies in developing more robust contingency plans. By understanding the nature of these extreme events, businesses can build resilience and better safeguard against future risks.

Finally, outliers can serve as a means of stress-testing machine learning models. By evaluating how models perform in the presence of extreme values, businesses can gain insights into the models' robustness and reliability under different scenarios. This kind of testing is particularly valuable for industries that deal with volatile data, such as stock trading or weather forecasting, where the ability to handle anomalies effectively can be a competitive advantage.

Conclusion

Overall, while outliers can present challenges in business-oriented machine learning tasks, they also hold the potential to reveal insights that drive innovation, mitigate risks, and improve decision-making. Properly addressing outliers through techniques such as detection, transformation, or specialized modeling approaches can enable businesses to leverage the full potential of their data while minimizing the downsides associated with extreme values.