Mastering the Two-Pointer Technique

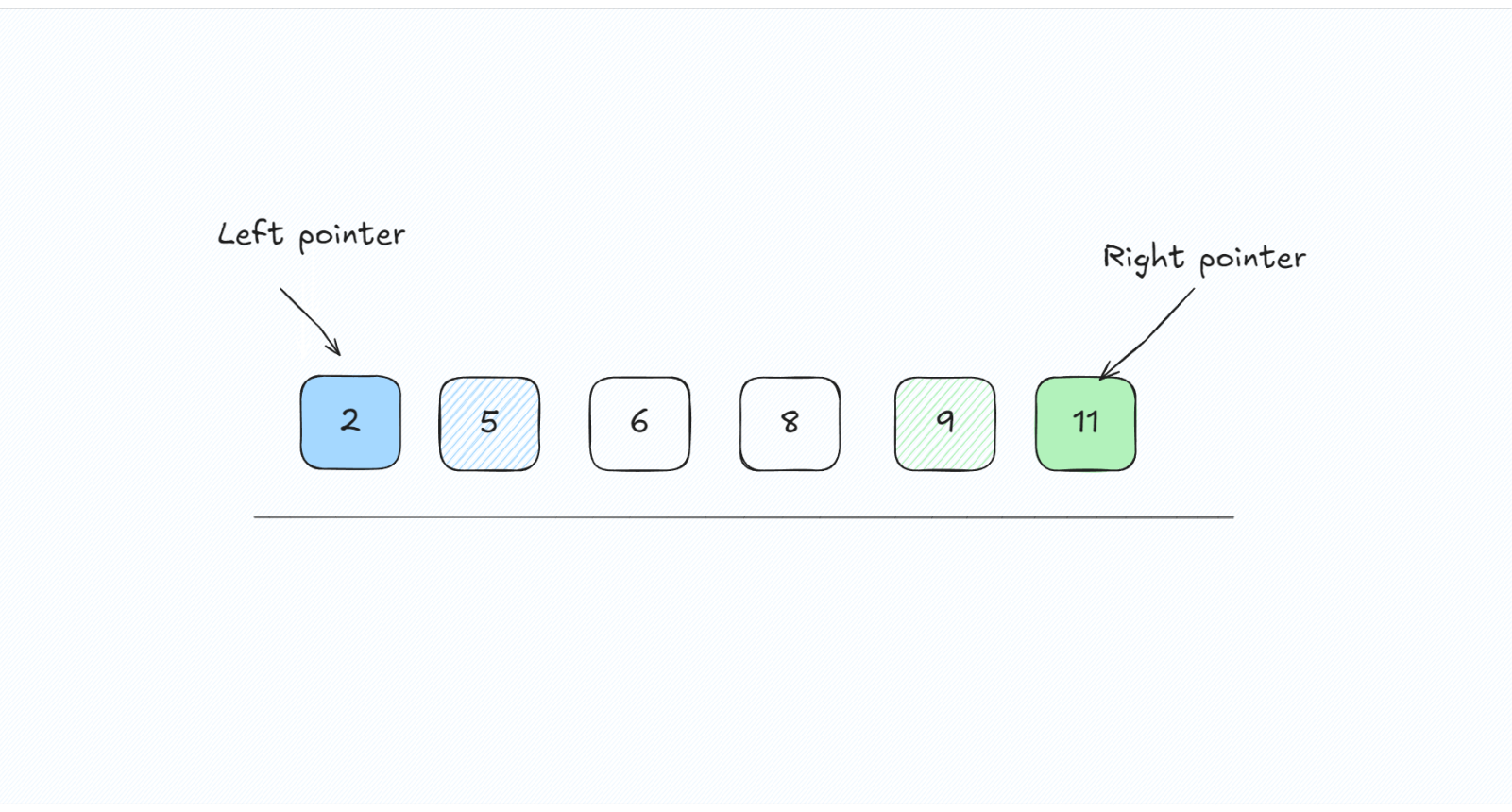
The two-pointer theory is a technique commonly used to solve array or linked list problems in a more efficient manner. Instead of using nested loops, which can increase the time complexity of a problem, two-pointer theory allows us to traverse the data structure in a single pass. This approach is particularly useful when aiming to reduce time complexity from O(n²) to O(n).

When Should You Use the Two-Pointer Technique?

The two-pointer approach is often employed in the following scenarios:

Finding pairs or triplets that meet specific conditions (e.g., two numbers summing up to a target value).
Working with sorted arrays: Sorting allows us to manipulate and adjust the pointers to quickly find solutions.
Reversing arrays or strings efficiently.
Detecting cycles in linked lists, like the famous Floyd’s cycle detection algorithm.
Merging two sorted arrays into one in O(n) time.
Comparing elements in an array or list to check for conditions such as palindromes, subsequences, or equality.

The two-pointer method shines in problems where iterating over an entire structure with conditions on pairs of elements can be optimized by systematically narrowing the scope of search with pointer movement.

Steps to Apply Two-Pointer Theory

Initialize Two Pointers: Set up your two pointers, typically at the start or end of the array/list, or one at each end.
Move the Pointers: Move them based on certain conditions related to the problem at hand.
Compare or Manipulate: Solve the problem by comparing or manipulating elements at the pointer positions.
Terminate: The process stops when the pointers meet or the desired condition is satisfied.

Example: Solving the Two-Sum Problem with Two Pointers

Let’s explore how the two-pointer technique can be applied by solving a classic problem—the Two Sum problem.

Problem: Given an array of integers nums and a target integer target, return the indices of the two numbers that add up to the target.

Example:

Input: nums = [2,7,11,15], target = 9
Output: [0, 1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Brute-Force Approach:

A common way to approach this would be to use two nested loops to check every possible pair in the array and return the indices of the pair that sum up to the target. While this works, the time complexity is O(n²), which isn't efficient for larger arrays.

Optimized Two-Pointer Approach:

Here’s how we can solve it using two pointers:

let leftP = 0;
let rightP = nums.length - 1;

while (leftP < rightP) {
  let sum = nums[leftP] + nums[rightP];
  if (sum === target) {
    return [leftP, rightP];
  } else if (sum < target) {
    // We need a larger sum, move the left pointer to the right
    leftP++;
  } else {
    // We need a smaller sum, move the right pointer to the left
    rightP--;
  }
}

Why Is This Efficient?

Single Traversal: Instead of checking all pairs, we efficiently narrow down the possibilities by adjusting the pointers.
Time Complexity: The time complexity is O(n), as we only traverse the array once by moving the pointers inward.
Space Complexity: This approach requires O(1) extra space, as no additional data structures are needed apart from the pointers.

Key Insights from the Example:

We start with two pointers, one at the beginning (leftP) and one at the end (rightP) of the array.
We check the sum of the values at both pointers.
If the sum matches the target, we return the indices.
If the sum is less than the target, we increment the left pointer to explore larger numbers.
If the sum is greater, we decrement the right pointer to explore smaller numbers.
This process continues until we find the correct pair or the pointers cross each other.

More Use Cases for Two-Pointer Technique

1. Reversing an Array

The two-pointer approach can also be used to reverse an array or string in-place with O(n) time complexity.

let arr = [1, 2, 3, 4, 5];
let left = 0;
let right = arr.length - 1;

while (left < right) {
  // Swap the values
  [arr[left], arr[right]] = [arr[right], arr[left]];

  // Move pointers inward
  left++;
  right--;
}

2. Cycle Detection in Linked Lists

Floyd's Tortoise and Hare algorithm is a two-pointer approach used to detect cycles in a linked list. One pointer moves slowly (one step at a time), while the other moves quickly (two steps at a time). If there is a cycle, the two pointers will eventually meet.

3. Merging Two Sorted Arrays

If you have two sorted arrays and want to merge them, two pointers can be used to traverse both arrays simultaneously, comparing elements and inserting them into a new array in sorted order.

let arr1 = [1, 3, 5];
let arr2 = [2, 4, 6];
let merged = [];

let i = 0, j = 0;

while (i < arr1.length && j < arr2.length) {
  if (arr1[i] < arr2[j]) {
    merged.push(arr1[i]);
    i++;
  } else {
    merged.push(arr2[j]);
    j++;
  }
}

// Append remaining elements
merged = [...merged, ...arr1.slice(i), ...arr2.slice(j)];

Conclusion

The two-pointer technique is a powerful tool that can simplify and optimize many common problems involving arrays, linked lists, and strings. By reducing unnecessary nested iterations, this approach can bring down the time complexity from O(n²) to O(n), making it highly efficient for large datasets. Whether you’re looking to detect cycles, merge arrays, or find specific pairs or subsets in data, mastering the two-pointer theory will help you solve these challenges more effectively.

Understanding the Two-Pointer Theory