Solving “Knight Moves 6” (Jane Street Puzzle, October 2024)
 Guillaume Lethuillier
Guillaume Lethuillier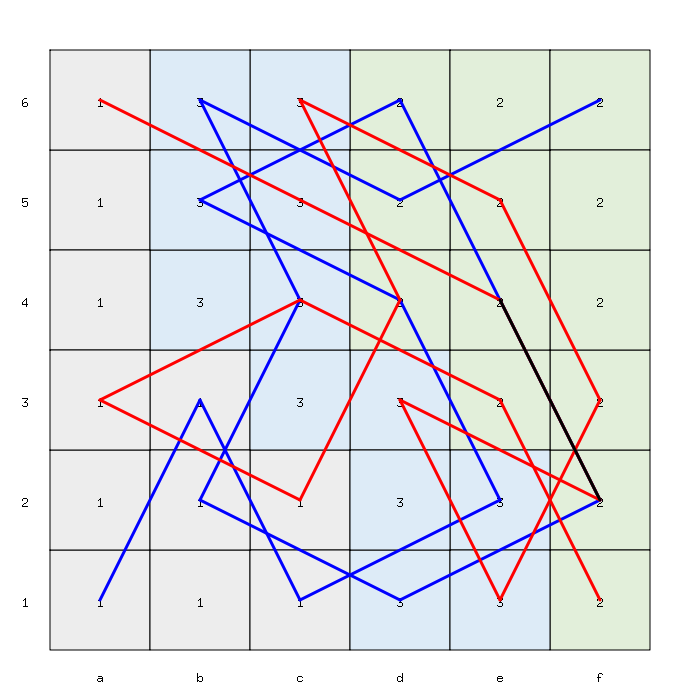
This puzzle is straightforward. As explained on the webpage, a 6x6 chessboard has squares labeled from A to C, corresponding to positive integers. The puzzle is solved by assigning values to A, B, and C and creating two corner-to-corner trips using knight’s moves so that each trip scores 2024. The method to calculate the score is: (a) moving between two different integers multiplies the score by the value the knight is moving to, and (b) moving between two identical integers increments the score with the value the knight is moving to. Last constraint: a square can only be visited once per trip (but a square does not necessarily have to be visited).
The official webpage distinguishes between optimal and trips which, while not optimal, are qualifying (i.e., A + B + C < 50).
To solve the puzzle, we developed a solver, accessible here, which generates random legal knight moves for each trip. The solver also produces combinations of ABC values that satisfy the constraint A + B + C < 50. It calculates the score corresponding to each combination of values for each path. When a score equals 2024, the solver verifies whether an opposing trip exists with the same values and score. If not, the trip is retained in memory until an opposing trip is found with the same values. However, if an opposing trip does exist, the two trips are evaluated against the global best score. If the total score is the lowest recorded, the combination of possible values is updated to ensure that their sum cannot exceed the best sum during the next exploration, thereby facilitating a rapid convergence toward the optimal solution.
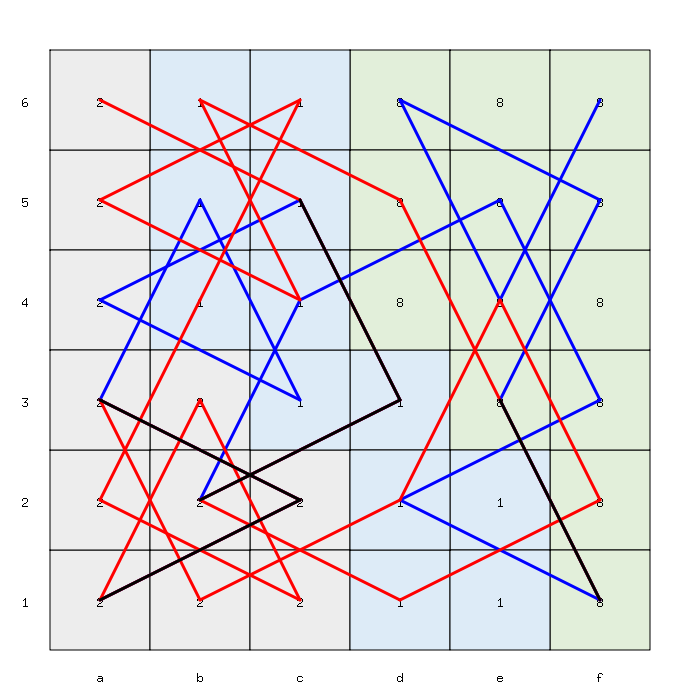
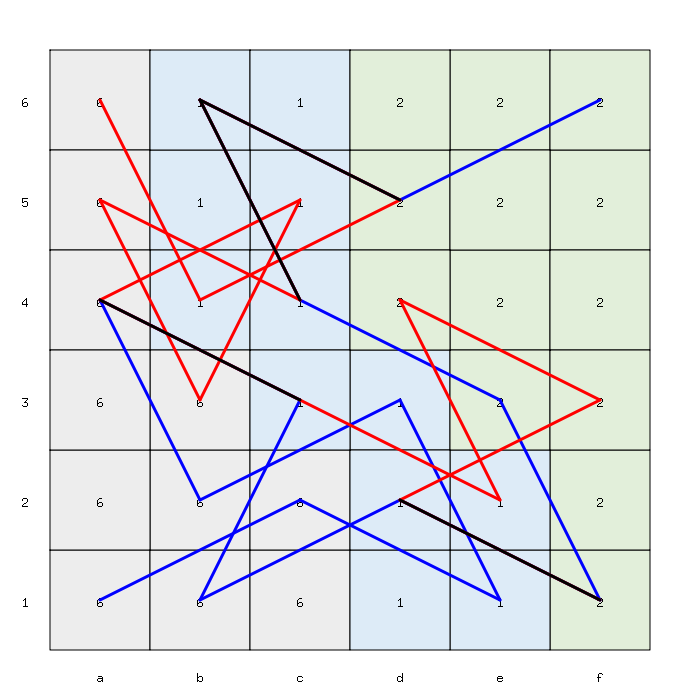
It appears that the best values correspond to the minimal sum 6 (A: 1, B: 3, C: 2) and the minimal trip length in terms of number of visited squares is 30, like in this example, rendered by the solver:
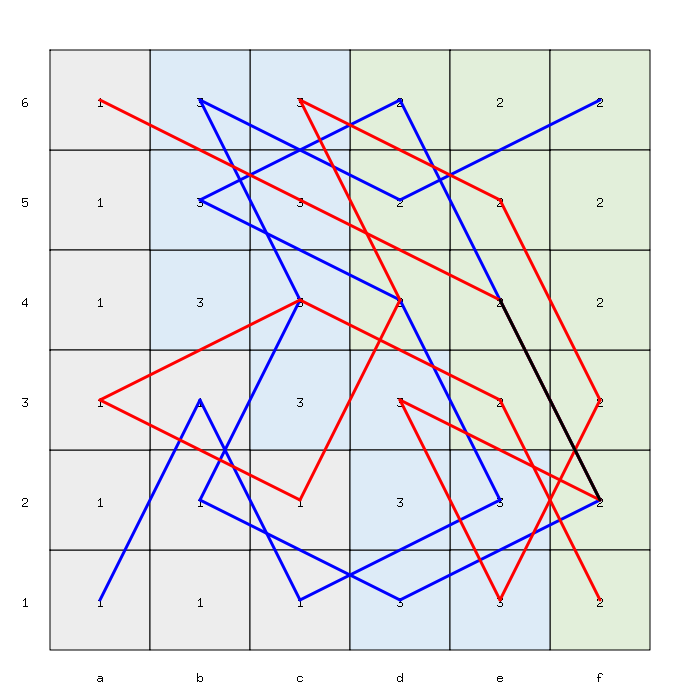
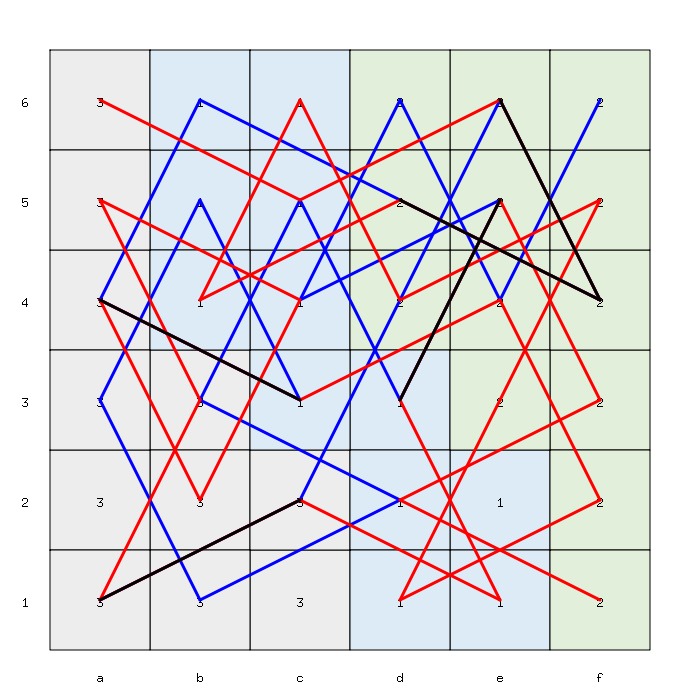
The solver has also identified several suboptimal solutions, as depicted below:
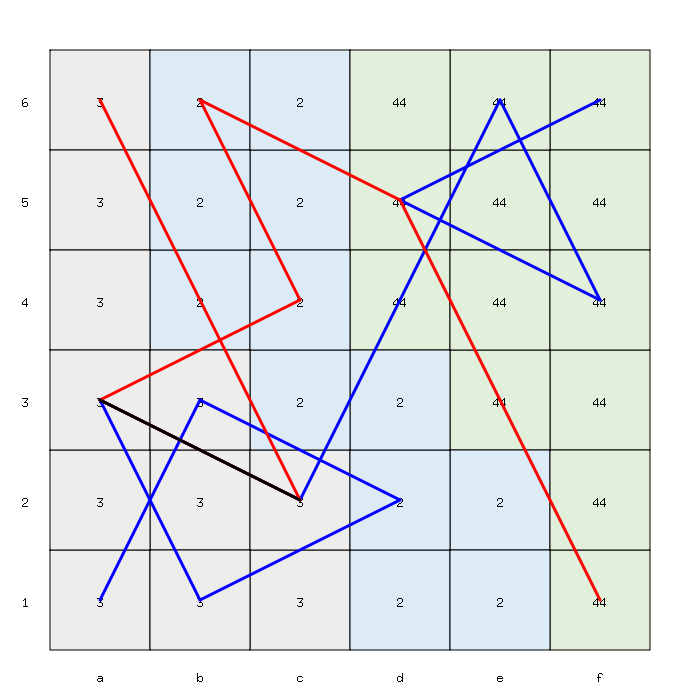
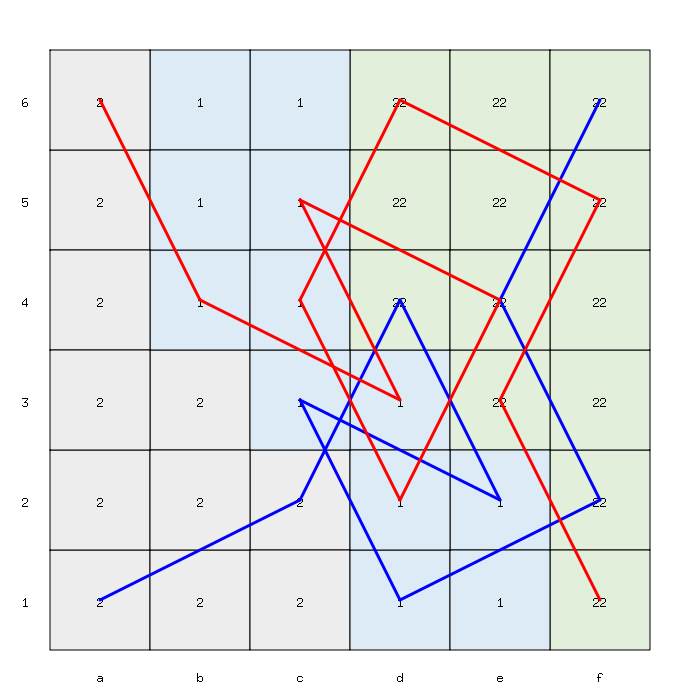
Subscribe to my newsletter
Read articles from Guillaume Lethuillier directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Guillaume Lethuillier
Guillaume Lethuillier
Opinions expressed in this blog are solely my own and do not express the views or opinions of my employer