This is the tenth part of a series of blog posts taking a deep look into Ada Lovelace's 1843 computer program, starting with Part 1: First Look at the First Program.

In a previous post I gave a summary of changes to Ada Lovelace’s table program that are required to make it run as fully intended. In this post, I’m going to expand on that to give what I understand to be an exhaustive list of all typos, bugs, and changes, whether or not they impact computation. This includes, for example, things that would be considered typos in the comments of modern source code.

I don’t mean to exaggerate the importance of these. An unimportant typo in a comment in modern source code would probably go completely unnoticed, but I think it’s important to have a full list in one place with some information about the change and its significance.

In this, I am largely building on the work of Rainer Glaschick, whose 2016 paper, “Ada Lovelace's Calculation of Bernoulli's Numbers,” gives his itemized list. I have found a few of my own to add and disagree with his determination on at least one. His list is broader than mine in a sense, though, as he talks about errors in the body of the text of “Notes” as well. My focus will be on just the table itself.

On the Source of Typos

I should add that one typo in the body of the text that Glaschick mentioned is worth drawing attention to. Lovelace signed each of her notes with her initials, “A.A.L” for Augusta Ada Lovelace, short for Augusta Ada King, countess of Lovelace. In her private correspondence with Babbage she states, “I mean to put A.A.L. to all the Notes.” (Ada, the Enchantress of Numbers: A Selection from the Letters of Lord Byron’s Daughter and Her Description of the First Computer, narrated and edited by Betty Alexandra Toole, p205, July 6, 1843)

Glaschick points out, though, that the final note, Note G, was printed with the initials “A.L.L.” on page 731.

This is notable because clearly Lovelace knows her own initials and would not likely have made the mistake herself. Without further evidence, the simplest explanation is that this was a typo on the part of the publisher. Likewise, in letters to Babbage she complained about a series of problems with the printers failing to make her corrections:

“I am beyond measure vexed to find that instead of inserting my corrected Table in the Revise … they have left it exactly as it was before. Out of several corrections made, not one is inserted;” Toole, p214

All of this is to say that at least some of the purely typographical errors are likely the fault of the printer and not Lovelace.

Overview of Table Fixes

There are over a dozen changes required to fully correct Lovelace’s table program. Of these, most are in the parts of the table that don’t impact computation and would be considered comments in modern source code. These look to be simple typographical errors. The correction is generally self-evident to make things consistent with the rest of the code.

There are four fixes that impact computation. The first is a simple change to the input data. The other three are bug fixes: one appears to be a simple typographical error likely due to the publisher, one appears to be a minor bug due to Lovelace, and one is a minor oversight that could be due to either.

Finally there are a few changes that aren’t simple typos or bugs but are required if the program is to compute “the Numbers to an indefinite extent, from the very beginning,” Lovelace’s full intent. Lovelace mentioned the use of what we might call auto-increment addressing in the text of Note G, but did use explicit notation for it in the table.

I’ll start with a summary of all of the changes required to get Lovelace’s program to run as intended. Continue reading for an in-depth explanation of each.

Fixes to Typos Not Impacting Computation:

• Operation 9: change the variable mentioned in “Indication …” column from “0v11=3v11” to “1v7=1v7”

• Operation 20: move formula in V11 trace column from operation 19 to operation 20 and replace “(2n-2)/3” with “(2n-2)/4”. Also move the “…” down from operation 19’s v10 trace column to operation 20.

• Operation 21: replace the “0” in the V11 variable trace column with “…“

• Operation 21: change the left-superscript of V12 in the “Variable receiving results” column from “0” to “2”.

• Operation 21: change the variable mentioned in “Indication of change in the value on any variable” column from “0v12=2v12” to “5v11=5v11”

• Operation 21: replace “(2n-2)/3” with “(2n-2)/4” in “Statement of Results”

• Operation 22: replace “A3” with “A0” in the V13 trace column

• Operation 24: replace the “…” in the V13 column with “0”

Fixes to Bugs Impacting Computation:

• Data. 1v3: change 4 to 1.

• Operation 4: replace “2v5 / 2v4” with “2v4 / 2v5” in the “Variables acted upon”

• Operation 24: The value from V13 should be negated. This involves replacing “+” with “-” in the “Nature of Operation,” and the “Variables acted upon” columns should be changed from “4V13 + 0V24” to “0V24 - 4V13”.

• Operation 25: add “3v11=0v11” to the “Indication …” column. Also add an additional “by a Variable card” to the “Statement of Results” column

Changes For Autoincrement Addressing

• Operation 10: add → for autoincrement to the use of 1V21 in the “Variables acted upon” column.

• Operation 21: change “1V22” to “1V21” and add → for autoincrement in the “Variables acted upon” column.

• Operation 24: change “0V24” to “0V21” and add → for autoincrement in the “Variables acted upon” column, and similarly “1V24” becomes “1V21” with an added → for autoincrement in the “Variables receiving results” column.

Original, Transcribed, and Corrected Tables

I’ve prepared a spreadsheet that contains the following sheets:

• Original Note G Table: a scanned image of the original published table

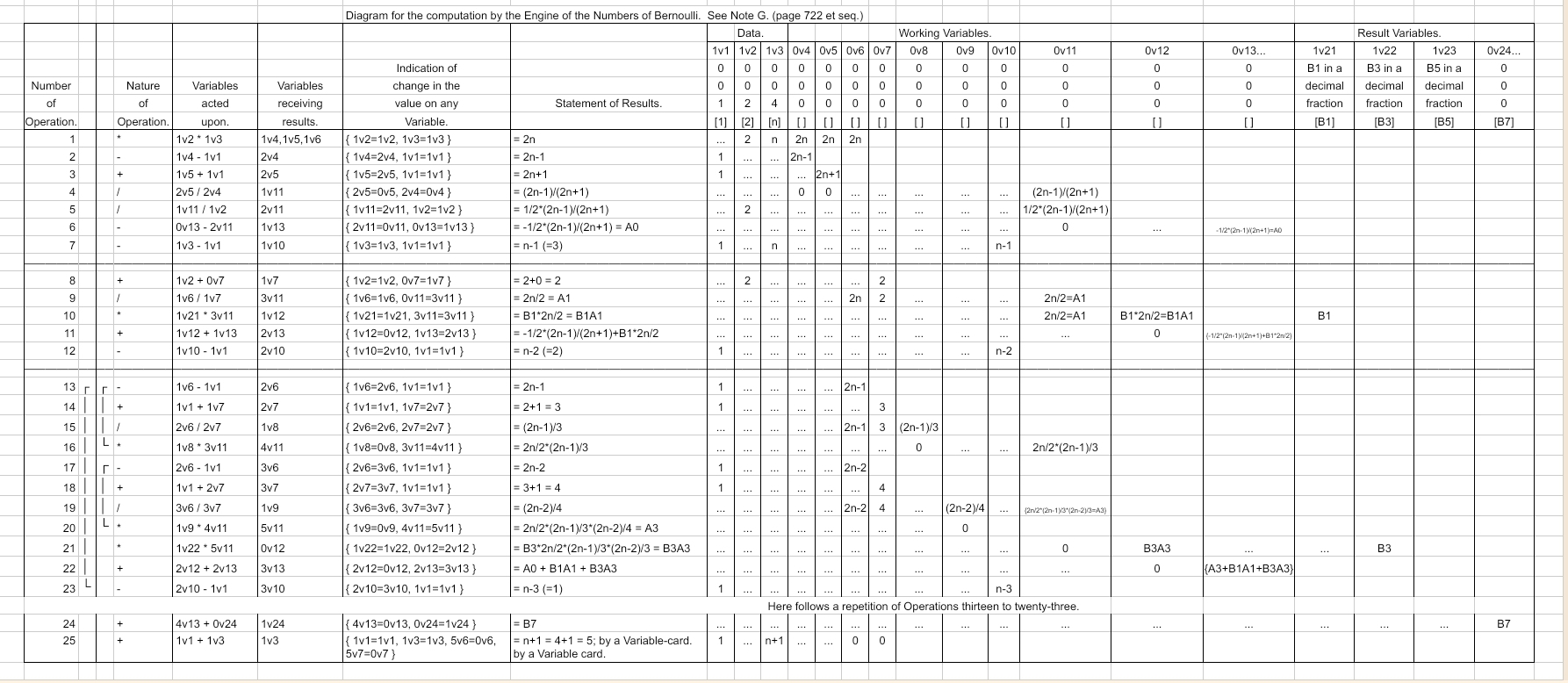
• TranscribedTableNoteG-NoCorrections: a literal transcription of the original published table, with no corrections

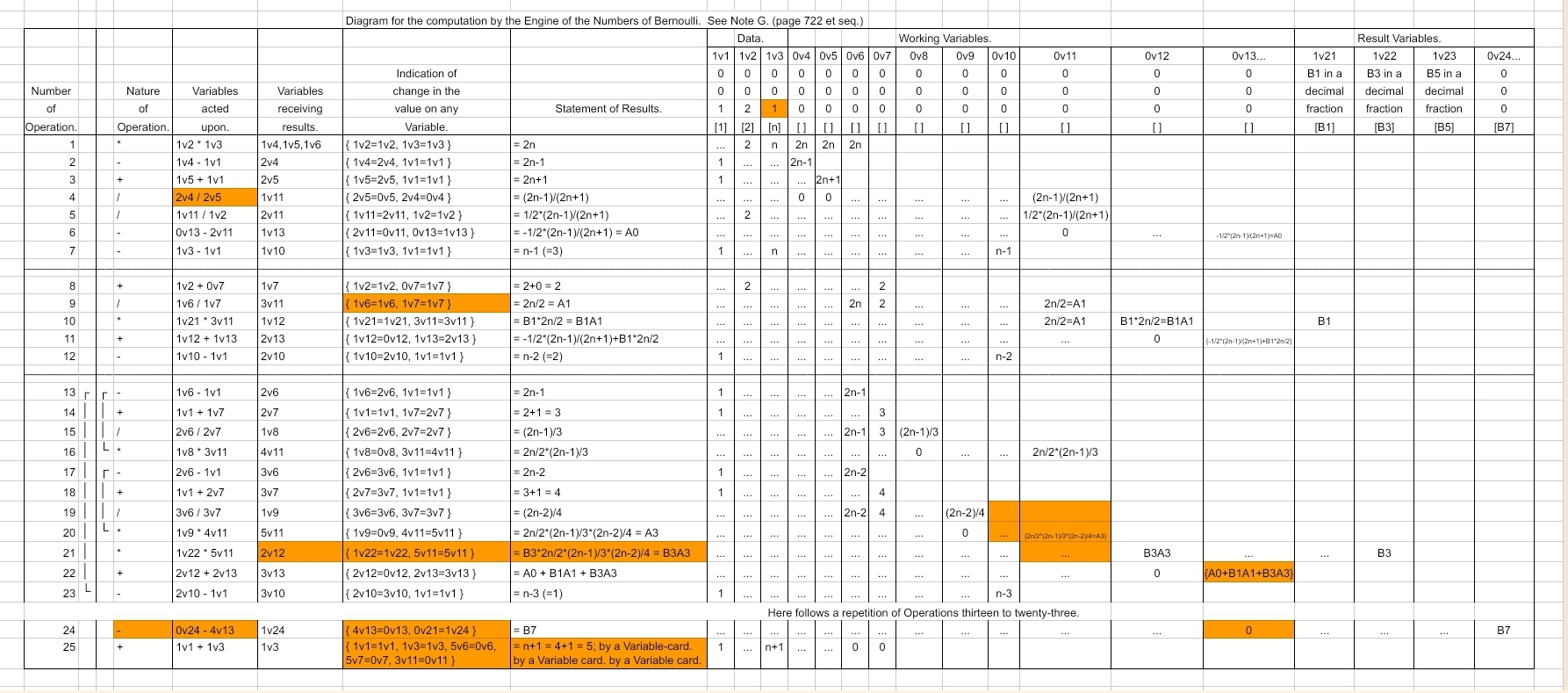
• TranscribedTableNoteG-WithCorrections: the transcription with all of the errors fixed, but no alterations for auto-increment indexing.

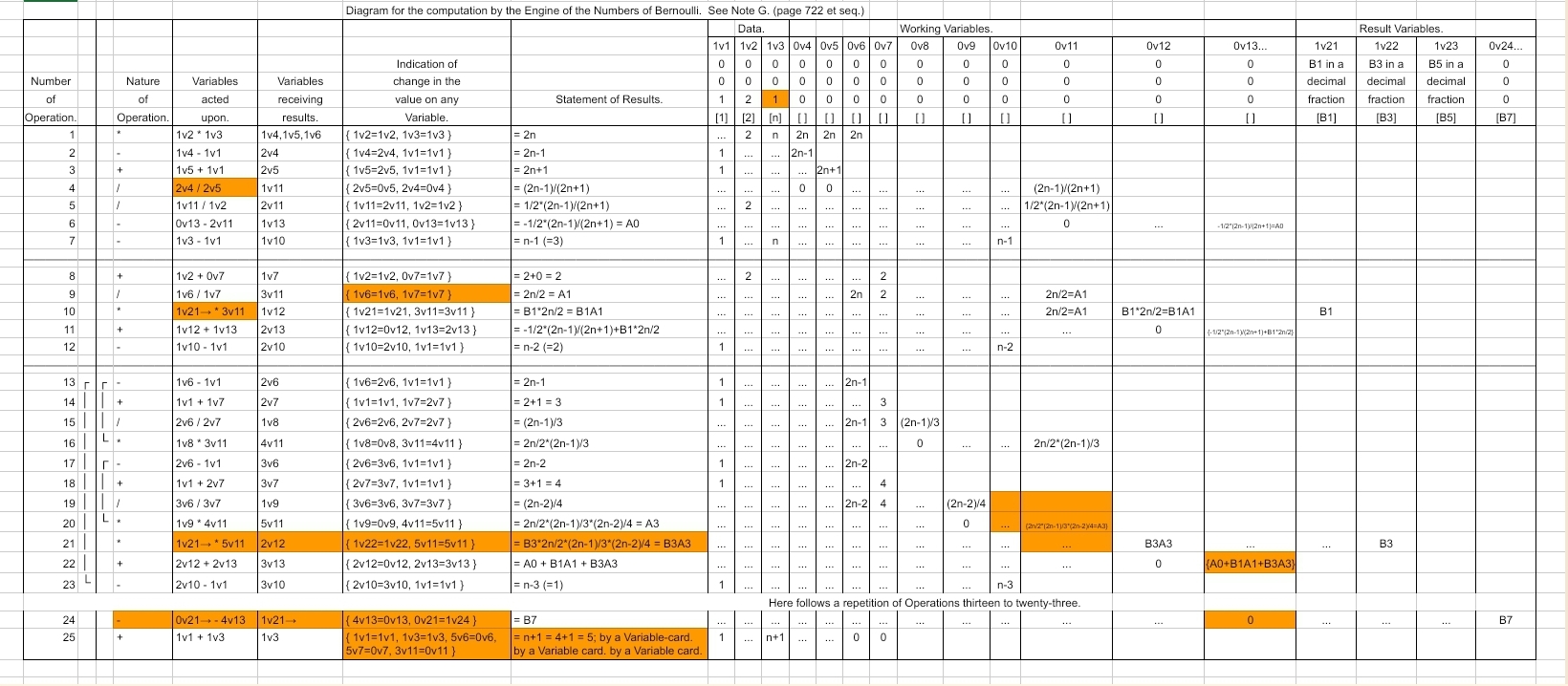
• TranscribedTableNoteG-WithCorrectionsAndAutoIncrement: the transcription with all errors fixed and also all alternations needed to support auto-increment indexing.

To verify it works, you can follow the steps from my earlier post to transliterate and run the final version from the “TranscribedTableNoteG-WithCorrectionsAndAutoIncrement” sheet. And sure enough, it still works.

The only difference between this final sheet and runnable version from my Part 7 post is the version linked above has all of the typos that don’t impact computation fixed as well.

Here is the original scan:

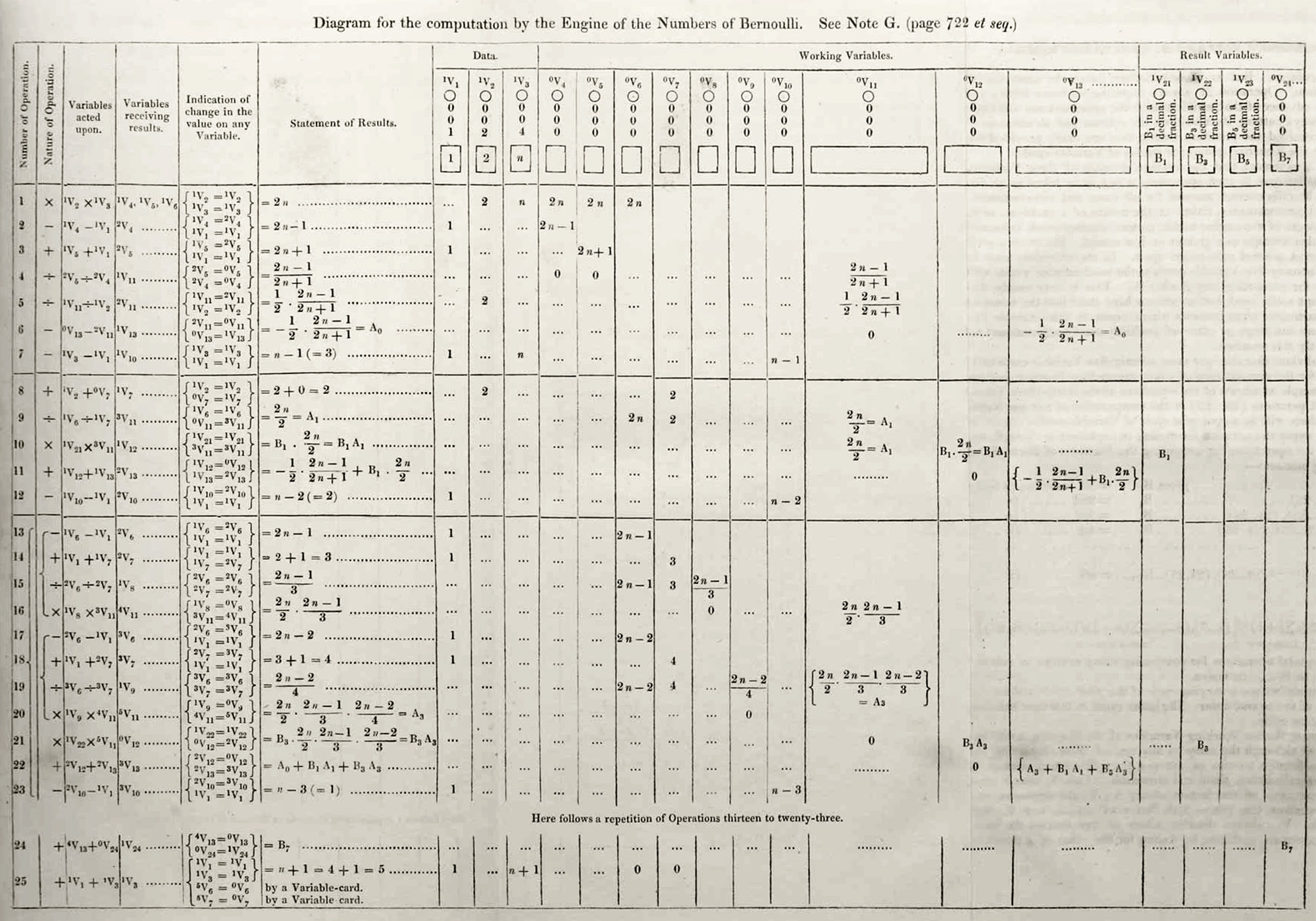
And the transcription without corrections:

And the transcription with corrections but without alterations for auto-increment addressing (differences from the original are highlighted in orange):

And finally, the transcription with corrections and also with alterations for auto-increment addressing:

Details

Here are more details for each of the fixes listed in the summary above.

Fixes to Typos Not Impacting Computation

I’ll start by looking at the fixes to typos that don’t impact computation. All of these are mistakes in notation that serves the purpose of modern comments. First, these are the fixes to the errors listed in Glaschick’s 2016 paper:

• Operation 21: replace the “0” in the V11 variable trace column with “…“

  • Zeros in the variable trace columns document the zeroing of a variable after use. This zeroing of variables is specified by listing the variable with a 0 left-superscript on the right side of an equals sign in the “Indication of change in the value on any Variable” column.

  • V11 is not reset to “0” in the “Indication …” column, so code that impacts computation does not reset V11 to zero. Additionally, it is clear from the rest of the code that the value in V11 is used in operation 16 in the next iteration of the loop, so it should not be reset to zero. Instead of “0”, “…” is used to document when a variable retains it’s value.

• Operation 21: change the left-superscript of V12 in the “Variable receiving results” column from “0” to “2”.

  • The convention used is the left-superscript on variables in the “Variables receiving results” column starts at 1 for the first time it is assigned something nonzero, and then every assignment after that has an incremented value showing that the variable has been destructively changed. A zero makes no sense in this context. The correct value is 2, since operation 10 first assigns it using 1V12. As a handwritten 2 can easily be mistaken for a 0, it seems likely this was the publisher’s typographical error.

• Operation 21: change the variable mentioned in “Indication of change in the value on any variable” column from “0v12=2v12” to “5v11=5v11”

  • This column documents whether variables in the “Variables acted upon” column retain their value, reset to zero, or receive a new result value (if they are also listed in the “Variables receiving results” column). Retaining value is marked by having the left-superscripts for a variable on both sides of the equals sign match and be nonzero. Resetting to zero is marked, as mentioned above, by using zero for the left-superscript on the right side of the equals. Receiving a new result is marked by incrementing a variable’s left-superscript—and for consistency, this is should only be done for variables listed in both “Variables acted upon” and “Indication of change in the value on any variable” columns.

  • To follow this convention, V12 shouldn’t be mentioned at all in this column since it is not mentioned in “Variables acted upon” and not expected to be zeroed. The variable, V11, is mentioned in “Variables acted upon” but was omitted from the “Indication …” column. All that remains is deciding on the left-superscripts to use. It is clear from the rest of the code that the value in V11 is used in operation 16 in the next iteration of the loop, so it should not be reset to zero. Following the convention, it should be “5v11=5v11”

  • Note: Glaschick says that it should be “5v11=3v11” which seems wrong as it doesn’t follow the convention of left-superscripts staying the same, incrementing, or being reset to zero. Ironically, I think Glaschick made his own typo in correcting Lovelace’s.

• Operation 24: replace the “…” in the V13 column with “0”

  • As mentioned above for operation 21, the convention is that a zero should occur in a variable’s trace column if and only if it is reset to zero in the “Indication…” column for that operation. In this case, V13 is reset to zero with “4V13=0V13”, and we can verify that it is assumed to be zero in operation 6 in the next iteration of the outer loop.

Glaschick also calls out the use of “1V3” in operation 25’s “Variables receiving results” and “Indication…” columns, suggesting it should arguably be “2V3”. He points out Lovelace’s reasonable argument:

however, Ada Lovelace argues that the values are for the next round of calculation and thus would have the upper index 1, because they are start values.

Perhaps this shouldn’t be considered an error so much as a awkward aspect of the left-superscript notation when used in loops:

The notation with the (constant) upper indices comes to its limits (or requires variables as upper indices and additional lines to keep track of these), once sequences of operations are repeated, because then the upper indices are dependent on the run.

In addition to the above errors, I identified a few more minor errors that don’t impact computation:

• Operation 9: change the variable mentioned in “Indication …” column from “0v11=3v11” to “1v7=1v7”

  • This is another instance of the mistake Glaschick identified in operation 21’s “Indication …” column. Following the convention, V11 isn’t listed in “Variables acted upon” so should not occur in “Indication …”. Meanwhile, V7 is listed in “Variables acted upon” and can be seen to be used later in operation 15, so it should not be reset to zero.

• Operation 20: move formula in V11 trace column from operation 19 to operation 20 and replace “(2n-2)/3” with “(2n-2)/4”. Also move the “…” down from operation 19’s v10 trace column to operation 20.

  • Operation 20’s “Statement of Results” is correct and in the correct place and matches the operations themselves. The trace should be fixed to match.

• Operation 21: replace “(2n-2)/3” with “(2n-2)/4” in “Statement of Results”

  • Operation 20’s “Statement of Results” is correct and operation 21 just needs to fix the typo to be consistent.

• Operation 22: replace “A3” with “A0” in the V13 trace column

  • Operation 22’s “Statement of Results” is correct and matches the operations themselves. The trace should be fixed to match.

Fixes to Bugs Impacting Computation

All of the above changes are fairly straightforward and minor. None of them change the computation performed. The remaining changes while minor, are serious in that they correct the computation itself.

These are fixes to errors impacting computation that were listed in Glaschick’s 2016 paper:

• Operation 4: replace “2v5 / 2v4” with “2v4 / 2v5” in the “Variables acted upon”

  • Much has been written about this transposition bug, I believe because it is the first bug one encounters when trying to run Lovelace’s program. The “Statement of Results” column for operations 2, 3, and 4 are correct. Likewise, the values listed in the variable trace columns for V4, V5, and V11 are correct. This fix just makes the operation consistent with the comments.

  • This might be the first bug in the published table program, but it seems more likely than not that this is a typo due to the publisher.

• Operation 24: The value from V13 should be negated. This involves replacing “+” with “-” in the “Nature of Operation,” and the “Variables acted upon” columns should be changed from “4V13 + 0V24” to “0V24 - 4V13”.

  • The left-superscript of V24 being zero indicates that it is expected to be zero. The operation as published would simply store V13 into V24, while subtracting V13 from V24 has the desired effect of storing -V13 into V24.

  • If the program is being run to only compute -B7, this change isn’t strictly necessary. One could change “Statement of Results” to be “= -B7” to be consistent, but this breaks everything if you try to compute “the Numbers to an indefinite extent, from the very beginning,” as Lovelace intended. In the next iteration of the loop, operation 21 will incorrectly use the negated Bernoulli number and get the wrong result.

  • Note: Glaschick says “in the 6th column it must read = -B7,” but this is not correct after making the change above.

• Operation 25: add “3v11=0v11” to the “Indication …” column. Also add an additional “by a Variable card” to the “Statement of Results” column

  • This is is necessary because V11 is expected to be zero in operation 4 in the next iteration of the outer loop. Remember, the Analytical Engine can’t be assumed to support destructive assignment as we’re used to on modern computers. As Glaschick explains, variables must be zero before being assigned to. If the variable receiving the result is also one “acted upon”, then this can be handled implicitly as part of the operation. Otherwise, the programmer must ensure it has been zeroed previously.

  • While generally, only variables listed in the “Variables acted upon” column, Lovelace used operation 25 to zero out both V6 and V7 for the next iteration of the outer loop. She indicated these with a special note “by a Variable card.” V11 should be zeroed in the same way if one intends to iterate the outer loop more than once. This appears to have been an oversight on the part of Lovelace.

This next change isn’t exactly a bug fix, but it is required if one wants to compute more than just B7.

• Data. 1v3: change 4 to 1.

  • The program is intended to compute “from the beginning” but the input, “Data,” variable, V3, is specified as initialized to “004” at the top. It is labeled “n” so it should start at 1, not 4.

  • Most of the table is a simultaneous view, not for any specific iteration, as you can see for the trace table values for V3 on operations 1 and 25. It is listed simply as “n” and "n+1” not the concrete 1 and 2 you’d expect for the very beginning or 4 and 5 for the iteration that calculates B7.

Changes For Autoincrement Addressing

Finally, if one wants to run Lovelace’s program as she intended, “indefinitely from the very beginning,” a few more changes are required. These require a bit of explanation.

In an earlier post I drew attention to Lovelace’s clear intent for Operation 21 and 24:

The only exception to a perfect identity in all the processes and columns used, for every repetition of Operations (13…23), is that Operation 21 always requires one of its factors from a new column, and Operation 24 always puts its result on a new column. But as these variations follow the same law at each repetition (Operation 21 always requiring its factor from a column one in advance of that which it used the previous time, and Operation 24 always putting its result on the column one in advance of that which received the previous result), they are easily provided for in arranging the recurring group (or cycle) of Variable-cards.

Babbage hadn’t yet designed a hardware implementation of that feature but assured Lovelace that it could be easily provided for, so she built her program for a virtual machine that assumed this auto-increment addressing functionality.

Unfortunately, not only was there no design for the hardware implementation, Babbage hadn’t devised a notation for it in the table language he had developed over the previous few years. In the most awkward aspect of the table, Lovelace chose to not add her own notation to the table itself.

Instead, in the table, for operations 10, 21, and 24 she listed the specific variables that would be used in just one iteration, a snapshot in time of the first time an operation is executed rather than a general simultaneous view, true of all iterations.

All three of these operations, in general terms, should be using V(21+i) where i increments by one after each operation it is used. For the specific iteration chosen, this works out to V21 on operation 10, then the first pass through the inner loop uses V22 on operation 21. If n starts at 4, then the inner loop from 13…23 will execute a second time using v23. Finally, after exiting the inner loop, operation 24 will use the next variable, V24. That’s why Lovelace chose those specific variables in the table.

Lovelace made this expectation of auto-increment addressing clear in the text of Note G, as quoted above.

Any new notation to make up for this awkwardness is arbitrary. To call it out as special and to minimize the alterations to the published table, I chose to append a right arrow, →, to the variables that are intended to use auto-increment addressing.

The final three changes required to compute "indefinitely from the very beginning" are then:

• Operation 10: add → for autoincrement to the use of 1V21 in the “Variables acted upon” column.

• Operation 21: change “1V22” to “1V21” and add → for autoincrement in the “Variables acted upon” column.

• Operation 24: change “0V24” to “0V21” and add → for autoincrement in the “Variables acted upon” column, and similarly “1V24” becomes “1V21” with an added → for autoincrement in the “Variables receiving results” column.

I’ve tried to identify an exhaustive list of all errors in the original table to put together here in one place. Please let me know if you find any I’ve missed or any errors in my error reporting!

In my next blog post, I’ll do some more exploring of the “language of the table”.