Pattern 1 : Fibbonacci like DP

This pattern is used where each decision depends on 1 or 2 previous states, just like Fibonacci sequence!

Climbing Stairs:

Leetcode Link

You can either climb 1 step or 2 steps at a time. Find how many distinct ways you can reach the top of a staircase with n steps.

DP Concept: The number of ways to reach the nth step is the sum of the ways to reach (n-1)th and (n-2)th steps (since you can come from either of those).

Example : Climbing stairs with 3 steps.

n= 0 (base case)

dp[0] = 1 (There's only one way to be at the bottom without climbing at all (this is our starting point)

n = 1

dp[1] = 1 (There's only one way to reach step 1 — you take a single step from the ground.)

n= 2

• Come from step 1 by taking 1 step.

• Come from step 0 by taking 2 steps.

So:

dp[2]=dp[1]+dp[0]=1+1=2

dp[2] = 2

There are 2 ways to reach step 2:

Take two 1-steps (1 + 1).

Take one 2-step

n= 3

• Come from step 2 by taking 1 step.

• Come from step 1 by taking 2 steps.

So:

dp[3]=dp[2]+dp[1]=2+1=3

dp[3] = 3

There are 3 ways to reach step 3:

Take three 1-steps (1 + 1 + 1).

Take one 1-step and one 2-step (1 + 2).

Take one 2-step and one 1-step (2 + 1)

Hence the general relation we get is :

d[i]=dp[i−1]+dp[i−2]

• To reach step i, you can either come from step i-1 (one step away) or from step i-2 (two steps away).

• So, the number of ways to reach step i is the sum of the number of ways to reach the previous step (i-1) and the number of ways to reach two steps below (i-2)

Top-Down Approach: Recursion with Memoization

In the top-down approach, we think of the problem as recursive. We attempt to solve the larger problem (e.g., reaching step n) by breaking it down into subproblems (e.g., reaching step n-1 and n-2), and we memoize (store) the results of subproblems to avoid recalculating them repeatedly.

class Solution {

    public int climbStairs(int n) {

        int memo[]= new int[n+1];
        Arrays.fill(memo,-1);
        return helper(n, memo);


    }
    int helper(int n , int memo[]){
        if(n==0 || n==1){
            return 1;
        }
        if(memo[n]!=-1) return memo[n];
        memo[n] = helper(n-1, memo) + helper(n-2, memo);
        return memo[n];
    }
}

• Memoization Setup: We initialize a memo array filled with -1 to store the number of ways to reach each step, where -1 indicates that the value hasn’t been computed yet.

• Base Cases: If n is 0 or 1, we return 1 because there’s only one way to reach those steps.

• Memoization Check: Before doing any calculations, we check if we’ve already computed the result for n. If so, we return it immediately.

• Recursive Calculation: If the value hasn’t been computed, we calculate it recursively by summing the ways to reach n-1 and n-2, then store the result in the memo array.

• Efficiency: This ensures that each step is only computed once, reducing the time complexity to O(n).

Bottom-Up Approach (Iterative DP)

The bottom-up approach, which I described earlier, builds the solution from the base cases (dp[0], dp[1]) upward, iterating through all steps until reaching the desired step n. It avoids recursion altogether.

class Solution {

    public int climbStairs(int n) {
        int dp[]= new int[n+1];
        dp[0] = 1;
        dp[1] =1;
        for(int i =2;i<=n;i++){
            dp[i] = dp[i-1] + dp [i-2];
        }
        return dp[n];
    } 
}

A simpler approach is using the bottom up approach. In this we just create an array of n + 1.

By now, we know that dp[0] =1 & dp[0] =1 so we only have one for loop from where we iterate from 2 until n and we use our transition relation that we found out earlier which is dp[I] = dp[i-1] + dp[i-2]

return dp[n].

Minimum cost climbing Stairs

You are given an array cost where each element represents the cost of stepping on a particular stair. You can either climb one step or two steps at a time, and your goal is to reach the top with the minimum cost. You can start from either step 0 or step 1.

Bottom - up approach:

Leetcode link

Youtube Video

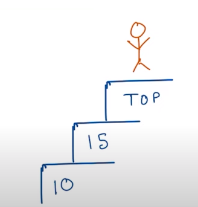
We have to reach top. (which is n+1) i.e one element after the last element.

In the Min Cost Climbing Stairs problem, you're asked to reach the top of the staircase, but the top is considered after the last step. This means you don’t pay the cost for the final "virtual" step (i = cost.length).

• The problem allows you to start either from step 0 or step 1, so you don't need to pay a cost to begin at either of these steps. This is why you initialize both dp[0] and dp[1] to 0.

    dp[0] = 0;
    dp[1] = 0;
  

Array: [10, 15, 20]

• It costs 0 to start at step 0 (ground level).

• It costs 0 to start at step 1.

• To calculate the cost to reach step 2 (the "top" step is actually after the last physical step, which is step 2), you can either come from:

  • Step 1 (take 1 step), or

  • Step 0 (take 2 steps directly to the top)

  • dp[2]=min(cost[1]+dp[1],cost[0]+dp[0]) = min(15+0,10+0)=10

• Step 3 is a virtual "top" step, and to calculate the minimum cost to reach the top, you can either come from:

  • Step 2 (take 1 step from step 2), or

  • Step 1 (take 2 steps from step 1).

  • dp[3]=min(cost[2]+dp[2],cost[1]+dp[1]) = min(20+10,15+0) = 15.

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int dp[] = new int[cost.length+1];
        dp[0] = 0;
        dp[1] = 0;

        for(int i = 2;i<=cost.length;i++){
            dp[i] = Math.min((cost[i-1]+dp[i-1]), (cost[i-2]+dp[i-2]));
        }
        return dp[cost.length];
    }
}