Introduction à l'Intelligence Artificielle

Bienvenue à nouveau dans cette série sur l'IA !

Dans l'article précédent, nous avons fait un bref aperçu des techniques et disciplines qui composent l'IA moderne, et nous avons terminé par une étude pratique de la régression linéaire.

Lorsque nous avons parlé de la régression linéaire simple, nous avons vu qu'il s'agissait de calculer une valeur numérique continue basée sur une variable du même type.

Dans ce cas, en partant d'une ou plusieurs variables numériques, nous serons capables de trouver une valeur discrète, c'est-à-dire une parmi un ensemble prédéfini de valeurs.

Disons que nous voulons déterminer la catégorie (ou la classe d'appartenance) d'une entité à partir de valeurs numériques en entrée.

Voyons en pratique ce que cela signifie et comment cela fonctionne.

Classification en Apprentissage Automatique

Dans le domaine de l'apprentissage automatique le terme "classification" est plus intuitif que celui de "régression". En effet, en ce cas l'objectif est d'assigner un objet à une ou plusieurs catégories (classes). Un exemple classique que nous rencontrons quotidiennement est celui de notre boîte mail, où les mécanismes de filtrage et de catégorisation fournis par notre service de messagerie électronique jouent un rôle essentiel dans la protection et l'organisation des courriels.

Dans cet article, nous nous concentrerons sur deux des principaux types de classification et sur les deux algorithmes les plus courants qui leur correspondent. Nous compléterons l'exposé par un exemple pratique (« hands-on ») en langage Python et en utilisant Google Colab comme environnement.

Classification binaire

La classification binaire en apprentissage automatique est un type de classification où le modèle prédit l'un des deux résultats possibles. L'objectif est de classifier les données en deux classes distinctes en se basant sur les caractéristiques d'entrée.

Supposons que nous avons un jeu de données comme dans la figure, qui montre la relation entre l'âge d'une personne et le fait qu'elle ait ou non acheté des chaussettes comme cadeau de Noël.

1 = achète les chaussettes, 0 = achète autre chose

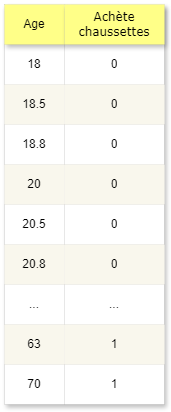
Nous voulons utiliser ces données pour savoir (prédire) si notre oncle Achille (qui a 37 ans) nous offrira ou non des chaussettes pour le prochain Noël.

D’abord essayons de modéliser le problème comme une régression linéaire (voir l'article sur la régression linéaire si besoin).

Prenons l'âge comme variable indépendante, X et la probabilité d'acheter des chaussettes sur l'axe y.

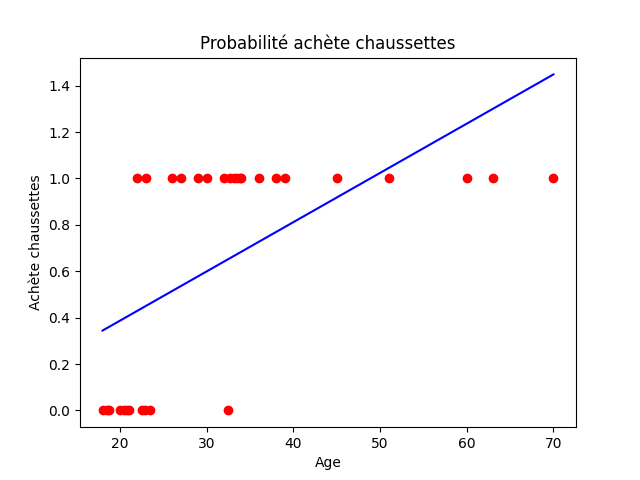
Nous pouvons immédiatement voir comment la droite générée par l'entraînement ne s'adapte pas bien aux données. En effet, bien qu'il y ait une relation claire entre l'âge et le fait de donner des chaussettes, notre droite est bien éloignée des valeurs actuelles et pourrait échouer dans la prédiction.

Essayons plutôt d'appliquer une autre technique, très courante: la régression logistique.

Régression Logistique

L'algorithme de classification binaire le plus représentatif est sans doute la régression logistique.

Le terme "régression" dans le nom n'est pas là par hasard ! En effet, si vous êtes familier avec la régression linéaire, vous remarquerez que la régression logistique n'est rien d'autre qu'un cas particulier où la variable cible n'a que deux valeurs possibles.

Tout d'abord, nous devons nous familiariser avec la fonction de base de cette technique, la fonction appelée Sigmoïde.

Fonction Sigmoïde

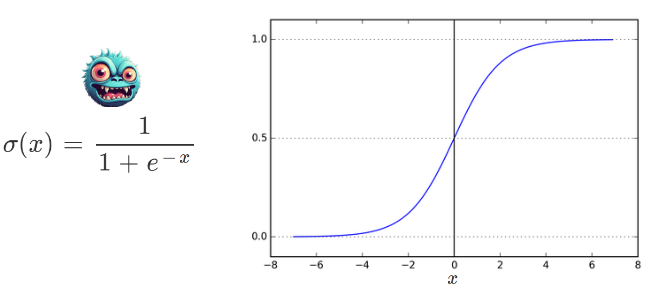
“e” est la base du logarithme naturel, approximativement égal à 2,71828.

La fonction sigmoïde prend n'importe quel nombre réel comme entrée et retourne une valeur comprise entre 0 et 1. Elle se rapproche de 0 lorsque l'entrée devient négative et de 1 lorsque l'entrée devient positive. Lorsque la variable x est 0, la fonction sigmoïde retourne 0,5.

Le petit monstre à côté de la formule sert à montrer qu'il y a des choses plus effrayantes que les maths !

Dans la figure, nous observons comment le graphique de cette fonction s'adapte beaucoup mieux à ce type de situation.

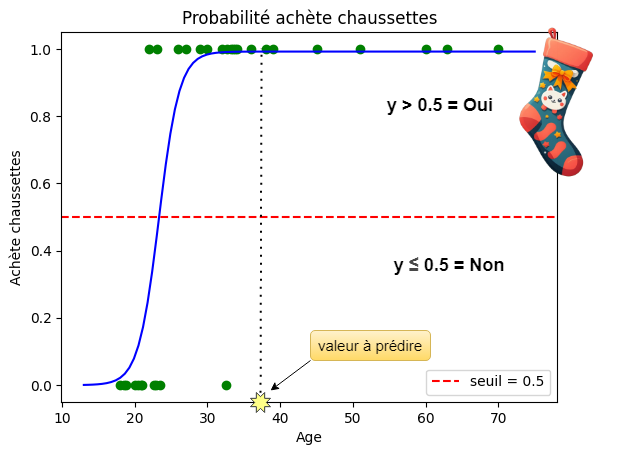
Tous les valeurs au-dessus du seuil de 0,5 sont considérées comme positives (achat) et les autres comme négatives (non achat).

La valeur 37 (les années du cher oncle) correspond à une valeur très proche de 1 et donc clairement positive, nous recevrons donc bien des chaussettes pour Noël (youpi !)

Afin que la sigmoïde s'adapte à nos données, nous avons utilisé la formule de la régression linéaire dans l'exposant :

$$f(x) = \frac 1 {1+e^{(a+b*x)}}$$

Cela nous montre comment les deux techniques sont étroitement liées.

Classification multi-classe

Nous avons vu comment prédire des valeurs binaires, mais que faire lorsqu'il y a plusieurs valeurs possibles ?

Supposons en effet d'avoir un ensemble de données comme dans la figure, où nous avons deux caractéristiques : la longueur de la queue, la longueur des oreilles, et trois types d'animaux : chat, chien et souris.

Nous pourrions utiliser un algorithme spécifique à la classification binaire et appliquer des techniques pour le généraliser, mais il est peut-être préférable d'en choisir un parmi ceux spécifiquement conçus pour la classification multi-classe.

Parmi les algorithmes les plus utilisés et les plus simples, nous avons le K-NN.

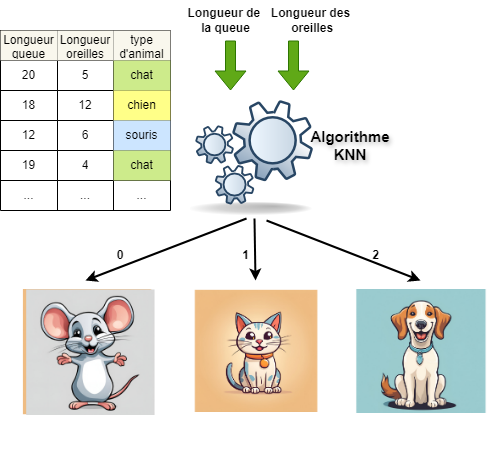
K-Nearest Neighbors

Cet algorithme (qui se traduit par voisins les plus proches) diffère un peu de ceux que nous avons traités jusqu'à présent. Il appartient toujours à la classe des algorithmes supervisés (ceux basés sur des données d'exemple qui spécifient à la fois l'entrée et la sortie), mais contrairement aux autres, il ne nécessite pas d'entraînement. En effet, il n'y a même pas de modèle au sens strict.

C'est ce qu'on appelle un algorithme lazy (paresseux), car il ne fait aucun effort tant qu'il n'y a pas de données à prédire (je l'appellerais plutôt un algorithme procrastinateur…). Nous pouvons représenter les données d'entraînement comme dans le graphique ci-dessous.

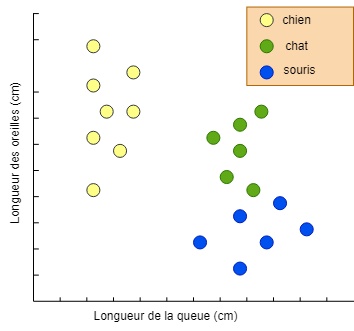
Sur les deux axes, nous voyons les deux valeurs d'entrée (features) et les couleurs représentent les différentes classes.

Comme déjà mentionné, dans ce cas, l'apprentissage ne génère pas de modèle ; le modèle sera le même ensemble de données. Lorsque nous devons trouver la classe d'appartenance d'un nouvel élément, le K-NN prend en compte les k points les plus « proches » et, en fonction de la majorité d'une classe, il prend sa décision.

Observons maintenant comment se comporte le K-NN si nous ajoutons une nouvelle valeur et devons la classifier. Dans l'illustration, nous avons ajouté une nouvelle observation (le point rouge) et nous voulons savoir de quel animal il s'agit.

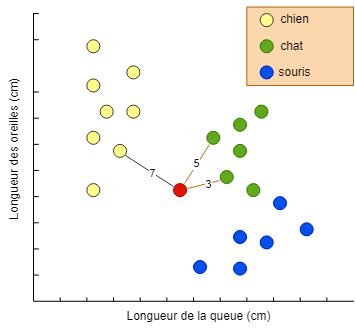
Nous avons choisi trois comme valeur de k, donc nous cherchons les trois points les plus proches parmi les données en notre possession (si vous avez déjà joué à la pétanque, ce calcul vous sera familier).

Nous voyons que deux des trois plus proches sont de couleur verte (chat) et le troisième est de couleur jaune (chien), donc l'animal est classé comme un chat.

Étude de cas – Gâteau d'anniversaire

Assez de théorie ! Passons à la pratique avec un véritable exemple tiré d'une histoire vraie, mais - comme dans les meilleurs films hollywoodiens - complètement inventée…

Votre compagnon/compagne a décidé de vous préparer un gâteau spécial et secret pour votre anniversaire de mariage. Vous êtes plein de joie en chemin vers l'épicerie, mais soudain, vous vous rendez compte que vous ne vous souvenez plus des ingrédients à acheter, bien qu'il/elle les ait répétés plusieurs fois (est-ce vrai quand elle vous accuse de ne pas écouter ?).

Vous pourriez appeler, mais vous ne voulez pas admettre votre oubli.

Il y a une meilleure option : vous vous rappelez de trois des ingrédients, peut-être pouvez-vous deviner de quel gâteau il s'agit et ainsi trouver les autres ingrédients nécessaires par vous-même.

Préparation du dataset

Une recherche en ligne de quelques heures (vous ne voulez vraiment pas abandonner…) vous permet de créer une petite table avec des gâteaux et des ingrédients issus de différentes recettes (notre dataset).

Vous savez que vous devez acheter (parmi les autres)

• une plaquette de beurre sucré

• 200 grammes de sucre de canne

• 110 grammes de yaourt grec

Selon nos recherches, nous savons que seuls trois types de gâteaux contiennent ces ingrédients en même temps.

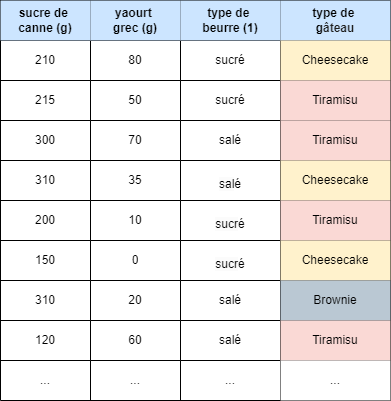
Quel algorithme appliquer ?

Nous nous retrouvons donc avec un vecteur tridimensionnel X comme suit :

X = [[210, 80, sucré], [215, 50, sucré], [300, 70, salé],[205, 35, salé], [310, 10, sucré], [200, 0, sucré], [150, 20, salé], [310, 60, salé], [120, 120, salé], [210, 40, sucré], [130, 50, salé], [150, 70, sucré], [210, 60, salé], [130, 120, salé], [200, 60, sucré], [70, 90, sucré], [90, 80, salé], [120, 80, salé], [190, 50, salé], [80, 60, sucré]]

et un vecteur pour la variable dépendante y

y = [Cheesecake, Tiramisu, Tiramisu, Cheesecake, Tiramisu, Cheesecake, Brownie, Tiramisu, Brownie, Cheesecake, Cheesecake, Brownie, Cheesecake, Brownie, Cheesecake, Brownie, Tiramisu, Brownie, Cheesecake, Brownie]

Maintenant, essayez de ne pas regarder la solution et choisissez l'algorithme qui semble le mieux s'adapter au problème.

Données catégorielles

Encore un instant ! Il y a encore une chose à faire. Voyez-vous la variable "type de beurre" ? Comme vous le remarquez, elle n'est pas numérique, mais c'est ce qu'on appelle une variable catégorielle. Les algorithmes de ML n'aiment généralement pas les variables non numériques, ce qui signifie qu'il faudra la convertir en un nombre. Dans notre cas, nous utiliserons 0 pour "sucré" et 1 pour "salé" pour simplifier, bien qu'il existe des techniques plus sophistiquées que nous aborderons dans un autre article, lorsque nous parlerons du prétraitement des données.

Notre ensemble de données pour X deviendra donc le suivant

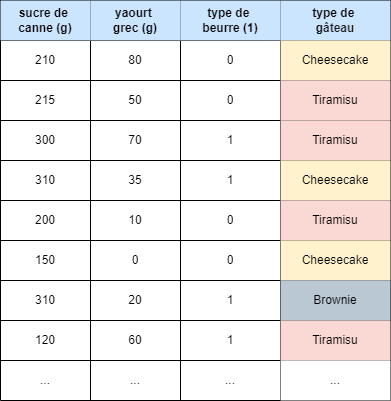
L'algorithme à utiliser (solution)

En regardant le problème, nous comprenons tout de suite qu'il ne s'agit pas d'une classification binaire puisque nous avons plus de deux valeurs cibles ; en fait, nous avons trois types de gâteaux possibles.

Nous sommes confrontés à un problème de classification multi-classe.

Dans ce cas, nous pouvons déjà exclure la régression logistique, car elle est normalement destinée à une utilisation en classification binaire.

Nous pourrions utiliser l'algorithme K-NN, puisque, par hasard, nous l'avons déjà abordé plus haut.

Hands-On !

Comme nous l'avons déjà fait par le passé, nous utiliserons Google Colab (un compte Google est nécessaire) pour nos expériences avec le code. Il vous suffira d'ouvrir un nouveau notebook et de copier le code pour faire vos tests.

Tout d'abord, mettons nos données dans une forme plus lisible pour notre modèle.

import numpy as np 
# Tableau avec trois colonnes représentant les valeurs des ingrédients 
# (chaque groupe de trois représente une ligne dans notre tableau)
X = np.array([
[210, 80, 0], [215, 50, 0], [300, 70, 1],[205, 35, 1], 
[310, 10, 0], [200, 0, 0], [150, 20, 1], [310, 60, 1], 
[120, 120, 1], [210, 40, 0], [130, 50, 1], [150, 70, 0], 
[210, 60, 1], [130, 120, 1], [200, 60, 0], [70, 90, 0], 
[90, 80, 1], [120, 80, 1], [190, 50, 1], [80, 60, 0]])

y = np.array(
['Cheesecake', 'Tiramisu', 'Tiramisu', 'Cheesecake', 
'Tiramisu', 'Cheesecake', 'Brownie', 'Tiramisu', 
'Brownie', 'Cheesecake', 'Cheesecake', 'Brownie', 
'Cheesecake', 'Brownie', 'Cheesecake', 'Brownie', 
'Tiramisu', 'Brownie', 'Cheesecake', 'Brownie'])

Maintenant, nous pouvons utiliser notre bibliothèque préférée (Scikit-learn) pour créer le modèle K-NN.

On importe la classe KNeighborsClassifier, celle qui implémente le K-NN et on lui spécifie trois paramètres (techniquement appelés hyper paramètres), comme le numéro K des voisins (cinq) et le type de métrique a utiliser; ‘minkowsky‘ et p = 2 c’est équivalent a la distance euclidienne.

from sklearn.neighbors import KNeighborsClassifier 
classifier = KNeighborsClassifier(n_neighbors = 5, metric = 'minkowski', p = 2)

Maintenant que le dataset est chargé en mémoire, nous pouvons l'utiliser pour prédire le type de gâteau en lui fournissant les trois ingrédients que nous connaissons

Mais arrêtons-nous un instant.

Une fois l'entraînement effectué, notre modèle commencera à faire des prédictions à droite et à gauche, mais comment pouvons-nous lui faire confiance ? Qui nous dit qu'il ne nous fera pas acheter les mauvais ingrédients ?

Évaluation du modèle

Il existe des techniques pour évaluer la qualité du modèle (et donc de nos choix en matière d'algorithme et de préparation des données).

La plus courante est la matrice de confusion (espérons qu'à la fin, la confusion ne soit que dans le nom).

Matrice de confusion

La matrice de confusion est un tableau utilisé pour évaluer les performances d'un modèle de classification. Elle montre la comparaison entre les valeurs prédites par le modèle et les valeurs réelles (les observations que nous avions) du dataset.

Elle comporte quatre éléments principaux :

• Vrai Positif (ex : un e-mail classé comme spam est réellement un spam)

• Faux Positif (ex : un e-mail classé comme spam est légitime)

• Vrai Négatif (ex : un e-mail classé comme légitime est réellement légitime)

• Faux Négatif (ex : un e-mail classé comme légitime est un spam)

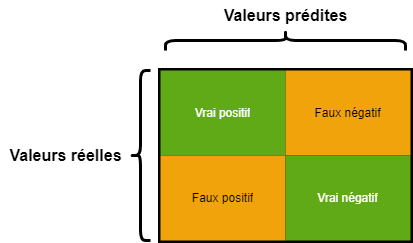
Sans entrer trop dans les détails du calcul de cette matrice, il est important de dire qu'elle nous permet de dériver des métriques importantes sur la qualité du modèle.

Prenons simplement la précision (accuracy) pour plus de simplicité. La précision d'un modèle est calculée comme suit :

$$Pr\acute{e}cision = \frac {VP + VN}{VP + VN + FP + FN}$$

Nous pouvons utiliser Python pour nos calculs.

# Appliquons d'abord notre modèle entraîné à nos données d'entraînement X
# et obtenons un tableau de prédictions 
y_pred = classifier.predict(X) 

# Normalement, ce tableau présente quelques différences avec les 
# étiquettes réelles, voyons cela ! 

# Valeurs réelles y
print (y.reshape(20,1)) 

['Cheesecake'] ['Tiramisu'] ['Tiramisu'] ['Cheesecake'] 
['Tiramisu'] ['Cheesecake'] ['Brownie'] ['Tiramisu']
 ['Brownie'] ['Cheesecake'] ['Cheesecake'] ['Brownie'] 
['Cheesecake'] ['Brownie'] ['Cheesecake'] ['Brownie'] 
['Tiramisu'] ['Brownie'] ['Cheesecake'] ['Brownie'] 

# Valeurs prédites 
print(y_pred.reshape(20,1))

['Cheesecake'] ['Cheesecake'] ['Tiramisu'] ['Cheesecake']
 ['Tiramisu'] ['Cheesecake'] ['Cheesecake'] ['Tiramisu'] 
['Brownie'] ['Cheesecake'] ['Brownie'] ['Brownie']
 ['Cheesecake'] ['Brownie'] ['Cheesecake'] ['Brownie'] 
['Brownie'] ['Brownie'] ['Cheesecake'] ['Brownie']

En comparant les données réelles avec les données prédites, nous pouvons voir où le modèle fait des erreurs. Dans ce cas, il a commis 4 erreurs de prédiction. Voyons la matrice de confusion générée et sa représentation graphique, avec bien in évidence les erreurs.

# créer la matrice de confusion en comparant les données réelles avec 
# les prédictions 
from sklearn.metrics import confusion_matrix, accuracy_score 
cm = confusion_matrix(y, y_pred) 
print(cm)

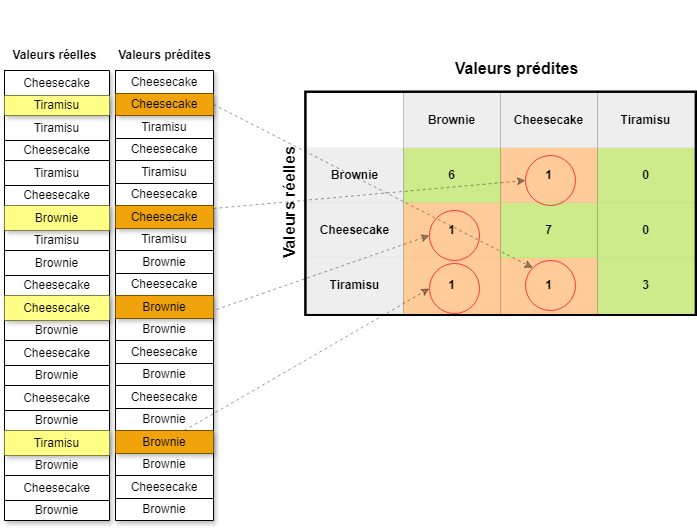
Calculons la précision maintenant en comparant les valeurs réelles (y) et les valeurs prédites par notre modèle (y_pred).

print(accuracy_score(y, y_pred))

Le résultat obtenu est de 0,8, ce qui correspond à 80 %, et cela peut être considéré comme bon dans notre cas.

Résultat

Tout est prêt ! Nous demandons (gentiment) à notre modèle K-NN de trouver avec quel gâteau nous nous régalons pour notre anniversaire de mariage.

Nous nous souvenons que les ingrédients dont nous étions certains étaient :

print(classifier.predict([[200, 110, 0]]))
resultat >>> ['Cheesecake']

Nous en mangerons donc un délicieux cheesecake et le tout sans avoir dérangé notre compagne ou compagnon !

Devoirs

La meilleure méthode pour apprendre est de pratiquer.

Essayez maintenant de refaire la même chose en utilisant un autre algorithme de classification multi-classe. Sur la page de Scikit-learn, vous trouverez tout ce dont vous avez besoin, en particulier dans la section sur les algorithmes de classification. Je vous suggère de commencer par l'Arbre de Décision.

Entraînez votre modèle et calculez la matrice de confusion pour obtenir la précision et voyez si vous pouvez faire mieux que 80% !

Conclusion :

Nous devrions à ce stade avoir une idée générale de ce qu'est la classification en apprentissage automatique et des problèmes qu'elle permet de résoudre. Nous savons également comment créer un modèle et mesurer sa précision sur un ensemble de données (ce qui sera également utile pour les problèmes de régression).

En regardant en arrière, nous pouvons dire que nous avons déjà parcouru un bon bout de chemin, et la route devant nous devient de plus en plus intéressante. Nous parlerons d'apprentissage non supervisé et puis poserons les bases pour l'exploration du deep learning, qui est au cœur de l'IA générative et des modèles de langage massifs (LLM), le tout en combinant, comme toujours, théorie et pratique, tout en laissant de côté – lorsque c'est possible – les détails mathématiques.

Je vous attends pour le prochain épisode, et d'ici là : bon apprentissage (automatique) !