Logistic Regression: A Gentle Introduction for Machine Learning Beginners

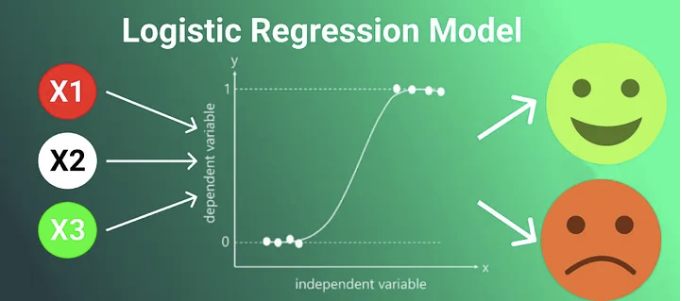
Have you ever wondered how machines make decisions? Whether it’s predicting if an email is spam, determining if a customer will buy a product, or estimating the likelihood of a disease, logistic regression plays a pivotal role in these predictions.

In this post, we’ll take a deep dive into logistic regression a powerful yet simple tool in your machine learning toolkit. Together, we’ll explore how it works, the math behind it, its strengths, limitations, and where it’s used. Whether you’re new to machine learning or brushing up on your knowledge, this guide will equip you with everything you need to know.

What Exactly is Logistic Regression?

At its core, logistic regression is a classification algorithm used to predict binary outcomes yes or no, true or false, 0 or 1. For instance:

• Will this customer churn?

• Is this transaction fraudulent?

• Does the patient have a disease?

Unlike linear regression, where we predict continuous values, logistic regression helps us predict the probability of a given outcome.

How Does Logistic Regression Work?

1. The Linear Foundation

Logistic regression starts with something simple: a linear equation that combines input features with their corresponding weights. Think of it as a way to calculate a score:

$$z=[ \log \left(\frac{P(y=1)}{1 - P(y=1)}\right) = \beta_0 + \beta_1 x_1 + \dots + \beta_n x_n ]$$

But here’s the twist: instead of predicting a continuous value like linear regression, logistic regression uses this score to predict a probability!

2. The Magic of the Sigmoid Function

To convert the score into a probability, logistic regression applies the sigmoid function:

$$\sigma(z) = \frac{1}{1 + e^{-z}}$$

This squeezes any value into a number between 0 and 1. If the result is closer to 1, the model predicts the positive class; if it’s closer to 0, it predicts the negative class. The decision boundary is usually set at 0.5.

3. Making a Prediction

Once we have the probability, we make a prediction:

$$y = \begin{cases} 1, & \text{if } P(y=1) \geq 0.5 \\ 0, & \text{if } P(y=1) < 0.5 \end{cases}$$

And just like that, we’ve classified our data point!

Interactive question: Can you think of a scenario in your daily life where predicting an outcome with a probability might help you make better decisions? Comment below!

Why ‘Logistic’ Regression?

The term logistic comes from the way this algorithm models the relationship between the input features and the log-odds of an event:

$$[ \log \left(\frac{P(y=1)}{1 - P(y=1)}\right) = \beta_0 + \beta_1 x_1 + \dots + \beta_n x_n ]$$

In simple terms, logistic regression predicts the logarithm of the odds that an event will happen, which is then transformed back into a probability.

Assumptions: What Should You Watch Out For?

Before jumping into logistic regression, there are a few assumptions you need to keep in mind:

1. Binary Outcome: The target variable should have two categories (0 or 1).

2. Independence: The observations must be independent of each other.

3. No Multicollinearity: Features shouldn’t be highly correlated.

4. Linearity in Log-Odds: Logistic regression assumes a linear relationship between the input features and the log-odds of the outcome.

Advantages and Limitations: When to Use Logistic Regression

Why Use Logistic Regression?

• Simplicity: It’s easy to implement and understand.

• Efficient: Logistic regression works well for smaller datasets.

• Probability Scores: Unlike many classification methods, it provides a probability estimate, which can be useful when you need confidence levels in your predictions.

• Fast to Train: Perfect for when you need quick results.

When Might It Struggle?

• Linearity: Logistic regression assumes that the relationship between features and the log-odds is linear, which might not always be the case.

• Outliers: It’s sensitive to outliers, which can skew the predictions.

• Non-linearity: If the data has complex, non-linear relationships, logistic regression might not capture the patterns effectively.

Quick question: Have you ever worked with a model that struggled to capture non-linear patterns? How did you solve it? Share your thoughts!

Evaluating the Performance of Logistic Regression

How do we know if logistic regression is doing a good job? Let’s look at some key evaluation metrics:

• Accuracy: How many predictions are correct?

• Precision & Recall: Precision is about how many of the positive predictions were correct, while recall is about how well the model identifies all the positive cases.

• F1 Score: A balance between precision and recall.

• ROC Curve & AUC: A great way to visualize the performance of a classification model by plotting the trade-off between the true positive and false positive rates.

To assess the quality of your logistic regression model, you might use a confusion matrix:

$$\begin{bmatrix} \text{True Positives (TP)} & \text{False Positives (FP)} \\ \text{False Negatives (FN)} & \text{True Negatives (TN)} \end{bmatrix}$$

• True Positives (TP): Correctly predicted positive cases.

• True Negatives (TN): Correctly predicted negative cases.

• False Positives (FP): Incorrectly predicted positive cases.

• False Negatives (FN): Incorrectly predicted negative cases.

Applications: Where is Logistic Regression Used?

Logistic regression is everywhere! Some common applications include:

• Healthcare: Predicting diseases based on symptoms and patient history.

• Finance: Estimating loan defaults or credit risks.

• Marketing: Predicting customer churn or response to campaigns.

• Spam Detection: Classifying emails as spam or not.

Wrapping Up

In summary, logistic regression is a simple yet powerful tool for binary classification tasks. Its ability to provide probability scores and interpret the relationship between features and outcomes makes it a versatile choice for many real-world problems.

Before you go, let me leave you with this question: How could logistic regression improve decision-making in your current projects? Whether you’re working with customer data, medical diagnostics, or finance, logistic regression could be the key to unlocking insights.

Call to Action

Loved this breakdown of logistic regression? Follow me for more deep dives into machine learning algorithms and practical data science tips!