Chapter 40: Dynamic Programming (Part 1)
 Rohit Gawande
Rohit GawandeTable of contents
- Introduction to Chapter :
- Introduction to Dynamic Programming (DP)
- Revisiting the Fibonacci Problem
- Fibonacci Code (Recursive Approach)
- Analyzing the Code
- Analyzing the Recursion Tree for n = 6
- Explanation of the Tree
- The Solution: Memoization
- Optimizing Fibonacci Using Dynamic Programming (Memoization)
- 1. What is Dynamic Programming (Definition)
- 2. Ways of Dynamic Programming
- 3. Seven Important Concepts in DP
- 4. Climbing Stairs Problem (Recursion)
- 5. Climbing Stairs (Memoization DP)
- 6. Climbing Stairs Variation
- 7. Climbing Stairs (Tabulation DP)
- Related Posts
- Related Series
- Connect With Me

Introduction to Chapter :
Dynamic Programming (DP) is a powerful technique for solving problems that involve overlapping subproblems and optimal substructure. It allows us to optimize recursive solutions by storing results of subproblems, preventing redundant computations, and thus reducing the overall time complexity.
In this chapter, we’ll explore the foundations of DP and look at one of the classic DP problems—Climbing Stairs—to illustrate different approaches such as recursion, memoization, and tabulation.
Introduction to Dynamic Programming (DP)
Dynamic Programming (DP) is a crucial concept in computer science, especially for solving problems efficiently. Earlier, we used various techniques in Data Structures and Algorithms (DSA) to solve problems, but DP allows us to approach these problems in a more optimized manner.
DP is particularly important for technical interviews, especially with major companies like FANG (Facebook, Amazon, Netflix, Google), where DP questions are frequently asked. Understanding DP is essential for cracking these interviews.
Let's walk through the process of solving the Fibonacci sequence using dynamic programming (DP) by analyzing the basic recursive approach, understanding why it’s inefficient, and then optimizing it using memoization. This explanation includes the code, the recursion tree, the memoization process, and the output in detail.
Revisiting the Fibonacci Problem

Fibonacci Code (Recursive Approach)
Here’s the code to calculate the Fibonacci number using a simple recursive method:
public class Fibonacci {
// Function to calculate the Fibonacci number recursively
public static int fib(int n) {
// Base case: if n is 0 or 1, return n
if (n == 1 || n == 0) {
return n;
}
// Recursive call
return fib(n - 1) + fib(n - 2);
}
public static void main(String[] args) {
// Output the 5th Fibonacci number
System.out.println(fib(5)); // Output: 5
}
}
Analyzing the Code
The recursive code is simple, but it’s inefficient for large inputs because it recalculates the same values multiple times. The time complexity is O(2^n), which is exponential, making the code impractical for larger values of n.
Analyzing the Recursion Tree for n = 6
Let’s visualize the recursion tree for fib(6) to understand the repeated calculations:
fib(6)
/ \
fib(5) fib(4)
/ \ / \
fib(4) fib(3) fib(3) fib(2)
/ \ / \ / \
fib(3) fib(2) fib(2) fib(1) fib(2) fib(1)
/ \ / \
fib(2) fib(1) fib(1) fib(0)
Explanation of the Tree
fib(6)callsfib(5)andfib(4).fib(5)callsfib(4)andfib(3).Notice that
fib(4)is called twice (once fromfib(6)and once fromfib(5)), andfib(3)is called three times.
This shows that the function calculates the same Fibonacci numbers multiple times, wasting time and resources. For example:
fib(2)is calculated five times.fib(3)is calculated three times.
The Solution: Memoization
To optimize this approach, we use memoization, where we store the results of subproblems (previously computed Fibonacci numbers) to avoid redundant calculations.
Optimizing Fibonacci Using Dynamic Programming (Memoization)
To optimize our approach, we use memoization, which is a top-down DP approach. Memoization stores the results of expensive function calls and reuses them when the same inputs occur again. Here’s the modified code:
Step 1: Understanding the Fibonacci Sequence with Memoization
We'll calculate fib(6) using memoization and visualize the recursion tree to understand how values are stored and reused. Memoization helps avoid redundant calculations by storing results of subproblems.
Step 2: Code Implementation
public class Fibonacci {
// Function to calculate Fibonacci number using memoization
public static int fib(int n, int[] f) {
// Base case: if n is 0 or 1, return n (first two Fibonacci numbers)
if (n == 1 || n == 0) {
return n;
}
// Check if fib(n) is already calculated and stored in the array
if (f[n] != 0) { // If f[n] is not 0, it means fib(n) is already computed
return f[n];
}
// Compute fib(n) recursively and store the result in the array
f[n] = fib(n - 1, f) + fib(n - 2, f);
return f[n]; // Return the stored value
}
public static void main(String[] args) {
int n = 6; // Calculate the 6th Fibonacci number
int[] f = new int[n + 1]; // Create an array to store Fibonacci values, size n+1
System.out.println("Fibonacci of " + n + " is: " + fib(n, f));
// Display the stored array values after computation
System.out.println("Memoization Array: ");
for (int i = 0; i <= n; i++) {
System.out.println("f[" + i + "] = " + f[i]);
}
}
}
Step 3: Explanation of the Code
Base Case:
- The base case returns
nwhennis 0 or 1. These are the first two numbers in the Fibonacci sequence.
- The base case returns
Memoization Check:
- Before computing
fib(n), the function checks iff[n]is already filled. If it's not0, the function returnsf[n]directly, avoiding redundant computation.
- Before computing
Recursive Calculation:
- If
f[n]is0, the function calculatesfib(n)by summingfib(n-1)andfib(n-2)and stores the result inf[n].
- If
Printing Results:
- The program prints the computed Fibonacci number and the memoization array to show how values were stored.
Step 4: Visualization of the Recursion Tree
For fib(6), the recursion tree with memoization is as follows:
fib(6)
/ \
fib(5) fib(4)
/ \ / \
fib(4) fib(3) fib(3) fib(2)
/ \ / \ / \
fib(3) fib(2) fib(2) fib(1) fib(2) fib(1)
/ \ / \ /
fib(2) fib(1) fib(1) fib(0)
fib(6) calls
fib(5)andfib(4).fib(5) calls
fib(4)andfib(3).Notice how
fib(4)andfib(3)are reused multiple times in the recursive approach, but with memoization, we avoid recalculating them by storing results.
Step 5: Filling the Memoization Array (f[])
As the function runs, the f[] array fills up. Here’s how it looks step by step:
Initial State: All values are
0(indicating they haven't been computed yet).f[] = [0, 0, 0, 0, 0, 0, 0]Step 1:
fib(0)andfib(1)are base cases:f[0] = 0 f[1] = 1Step 2: Compute
fib(2) = fib(1) + fib(0) = 1f[2] = 1 f[] = [0, 1, 1, 0, 0, 0, 0]Step 3: Compute
fib(3) = fib(2) + fib(1) = 2f[3] = 2 f[] = [0, 1, 1, 2, 0, 0, 0]Step 4: Compute
fib(4) = fib(3) + fib(2) = 3f[4] = 3 f[] = [0, 1, 1, 2, 3, 0, 0]Step 5: Compute
fib(5) = fib(4) + fib(3) = 5f[5] = 5 f[] = [0, 1, 1, 2, 3, 5, 0]Step 6: Compute
fib(6) = fib(5) + fib(4) = 8f[6] = 8 f[] = [0, 1, 1, 2, 3, 5, 8]
Step 6: Output and Memoization Array
When you run the code, the output and memoization array will look like this:
Fibonacci of 6 is: 8
Memoization Array:
f[0] = 0
f[1] = 1
f[2] = 1
f[3] = 2
f[4] = 3
f[5] = 5
f[6] = 8
Step 7: Explanation of How Memoization Works
In this approach, the memoization array (
f[]) stores the values offib(n)as they are computed.Whenever
fib(n)is called, the function first checks if the value already exists in the array:If it does, it uses the stored value, avoiding redundant recursive calls.
If not, it calculates
fib(n), stores it inf[n], and returns the result.
This reduces the time complexity from
O(2^n)(exponential) toO(n)(linear) because each value is computed only once and stored.
If you want to calculate:
fib(6)
You’ll need to store and access:
fib(0), fib(1), fib(2), fib(3), fib(4), fib(5), fib(6)
That's 7 values in total, and their indexes go from 0 to 6.
So, we must declare:
int[] f = new int[n + 1]; // which means new int[7];
❌ If we write int[] f = new int[n]; (i.e., new int[6]):
That gives indexes
0to5only.So, when we try to store or access
f[6], it will cause:
javaCopy codeArrayIndexOutOfBoundsException
Why This Works: The Principle Behind Memoization
Memoization identifies overlapping subproblems and reuses their results. By storing intermediate results:
We avoid repeated computations.
We transform the recursive approach into a much faster algorithm.
This is called Dynamic Programming, and memoization is one way to implement it efficiently.
By understanding the memoization technique and applying it to the Fibonacci sequence, we’ve demonstrated how DP optimizes computations.
1. What is Dynamic Programming (Definition)
Understanding Dynamic Programming (DP)
Dynamic Programming (DP) is a powerful optimization technique used in computer science to solve complex problems by breaking them down into simpler subproblems. It is particularly useful for problems that exhibit overlapping subproblems and optimal substructure properties.
1. What is Dynamic Programming?
Dynamic Programming (DP) is essentially optimized recursion. Instead of solving the same subproblem multiple times, DP stores the results of subproblems to avoid redundant computations, leading to significant improvements in efficiency.
2. Key Characteristics of DP
A. Optimal Problem
Dynamic Programming is applicable when we are dealing with an optimal substructure, which means that the optimal solution to the overall problem can be constructed from optimal solutions to its subproblems. This property is similar to what we learned in the Greedy Algorithm chapter, where we often look for local optima.
B. Multiple Choices
When approaching a problem, if there are multiple choices or branches in the recursion tree, it is an indication that the problem could potentially be solved using Dynamic Programming. The idea is to explore different combinations of choices and keep track of the optimal solutions.
3. Identifying Dynamic Programming Problems
To identify whether a problem can be solved using DP, check for the following:
Optimal Substructure: Can you derive the optimal solution to the problem by combining optimal solutions of its subproblems?
Overlapping Subproblems: Does the problem involve solving the same subproblem multiple times? If so, memoization or tabulation can be applied to save the results of these subproblems.
4. Example: Calculating the Sum of First n Natural Numbers
To illustrate the idea of recursion vs. dynamic programming, let’s consider the problem of calculating the sum of the first n natural numbers, represented as sum(n).
Recursive Approach
Recursive Function Definition:
If ( n = 1 ), return ( 1 ).
Otherwise, return ( n + sum(n - 1) ).
Recursive Tree Visualization:
sum(5)
|
sum(4)
|
sum(3)
|
sum(2)
|
sum(1)
|
return 1
In this case, the recursive calls create a skewed tree where each call only branches to one other call. Here, there is only one branch, and the recursion does not benefit from overlapping subproblems. Thus, it does not fit the criteria for DP.
5. When to Use Dynamic Programming?
If we had a more complex problem, such as calculating Fibonacci numbers, it would involve overlapping subproblems:
Fibonacci Recursive Function:
F(n) = F(n-1) + F(n-2)
Recursive Tree Visualization for Fibonacci:
F(5)
/ \
F(4) F(3)
/ \ / \
F(3) F(2) F(2) F(1)
/ \
F(2) F(1)
Here, you can see that the same subproblems (F(2) and F(3)) are solved multiple times. This makes Fibonacci a prime candidate for Dynamic Programming, where we can store the results of previously computed Fibonacci numbers and reuse them.
6. Definition of Dynamic Programming
Dynamic Programming is a technique in computer programming that helps to efficiently solve a class of problems that have:
Overlapping Subproblems: The problem can be broken down into smaller, reusable subproblems.
Optimal Substructure Property: An optimal solution can be constructed from optimal solutions of its subproblems.
Dynamic Programming is a critical concept in algorithm design and optimization. By recognizing when to use DP, you can transform exponential time complexity problems into polynomial time complexities, making it possible to solve larger and more complex problems efficiently. Always look for overlapping subproblems and optimal substructures to determine if DP is the right approach for your problem!
2. Ways of Dynamic Programming
Dynamic Programming (DP) is a method for solving complex problems by breaking them down into simpler subproblems. DP helps optimize solutions by storing intermediate results, either through Memoization (Top-Down) or Tabulation (Bottom-Up). Let’s explore both methods, focusing on the Tabulation approach with a step-by-step explanation, and an analysis of time complexity.
Ways of Dynamic Programming (DP)
Memoization (Top-Down Approach):
In this approach, recursion is used to solve the problem. Subproblem results are stored in a storage (usually an array or a hashmap) to avoid redundant calculations.
We’ve already seen this with the Fibonacci problem.
Steps:
Step 1: Use recursion to solve the problem.
Step 2: Store subproblem results to reuse them instead of recalculating.
Tabulation (Bottom-Up Approach):Absolutely! Let's dive deeper into Tabulation, a core concept of Dynamic Programming (DP), and understand it step by step with visualizations and examples to build a solid understanding.
2. Tabulation (Bottom-Up Approach)
Tabulation is a bottom-up approach to solving DP problems. Unlike memoization, which uses recursion and fills the DP table as needed (top-down), tabulation uses iteration and fills the DP table iteratively from the smallest subproblem to the largest. It eliminates the overhead of recursive function calls and prevents stack overflow issues that might occur in deep recursion.
Here's how we structure the tabulation method and apply it step by step.
Steps to Solve a Problem Using Tabulation
Identify the Subproblems:
- Break the main problem into smaller subproblems. Each subproblem should build upon the previous ones. The goal is to fill a table (typically an array) where each entry represents the solution to one of these subproblems.
Define the Table (Array):
Create a table (often called
dp[]) where each index represents a specific subproblem.The size of the table is usually based on the input size (
n) because we solve the problem up ton.Initialize the table with base cases (values that are known and can be directly assigned).
Iteratively Fill the Table:
Start filling the table from the smallest subproblem to the largest.
Use the known values from earlier indices in the table to calculate the values for the current index.
Continue until the table is completely filled.
Return the Final Solution:
- The final solution is typically stored at the last index of the table (
dp[n]), representing the solution to the original problem.
- The final solution is typically stored at the last index of the table (
Applying Tabulation to the Fibonacci Sequence
To make this clearer, let's revisit the Fibonacci sequence problem, using the tabulation method in detail.
Problem Recap: Fibonacci Sequence
The Fibonacci sequence is defined as:

The goal is to calculate the nth Fibonacci number.
Tabulation Steps for Fibonacci
Identify the Subproblems:
- Each Fibonacci number depends on the previous two numbers. So, for
Fib(n), the subproblems areFib(n-1)andFib(n-2).
- Each Fibonacci number depends on the previous two numbers. So, for
Define the Table (Array):
Create an array
dp[]of sizen + 1to store the Fibonacci numbers from0ton.The base cases are:
dp[0] = 0(0th Fibonacci number)dp[1] = 1(1st Fibonacci number)
Iteratively Fill the Table:
- Start from
i = 2and fill the table up toi = nusing the formula:
- Start from
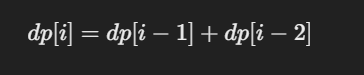
For example:
dp[2] = dp[1] + dp[0] = 1 + 0 = 1dp[3] = dp[2] + dp[1] = 1 + 1 = 2dp[4] = dp[3] + dp[2] = 2 + 1 = 3And so on.
- Return the Final Solution:
The final solution will be in
dp[n].
Full Code Implementation with Comments
public class TabulFib {
// Function to calculate Fibonacci using the Tabulation approach
public static int tabulfib(int n) {
// Step 1: Initialize a dp array of size n+1 to store the Fibonacci numbers
int dp[] = new int[n + 1];
// Step 2: Assign base values: dp[0] = 0, dp[1] = 1
dp[0] = 0;
dp[1] = 1;
// Step 3: Fill the dp array iteratively from dp[2] to dp[n]
for (int i = 2; i <= n; i++) {
// dp[i] is the sum of the two preceding values
dp[i] = dp[i - 1] + dp[i - 2];
}
// Return the nth Fibonacci number
return dp[n];
}
public static void main(String[] args) {
int n = 5; // Calculate the 5th Fibonacci number
// Print the result with a message for clarity
System.out.println("The " + n + "th Fibonacci number using Tabulation is: " + tabulfib(n));
}
}
Detailed Visualization of the Table Filling Process (Step-by-Step)
Let’s walk through the code for ( n = 5 ):
Initialize
dp[]:dp = [0, 1, _, _, _, _]dp[2] = dp[1] + dp[0] = 1 + 0 = 1:dp = [0, 1, 1, _, _, _]dp[3] = dp[2] + dp[1] = 1 + 1 = 2:dp = [0, 1, 1, 2, _, _]dp[4] = dp[3] + dp[2] = 2 + 1 = 3:dp = [0, 1, 1, 2, 3, _]dp[5] = dp[4] + dp[3] = 3 + 2 = 5:dp = [0, 1, 1, 2, 3, 5]
The final value, dp[5], is 5, which is the 5th Fibonacci number.
Time Complexity Analysis
The time complexity of this approach is O(n) because we fill the
dparray withnentries, and each entry takes constant time.This is much more efficient than the recursive approach, which has an exponential time complexity of O(2^n).
Space Complexity Analysis
The space complexity is O(n), as we use an array of size
n + 1to store the Fibonacci numbers.However, this can be optimized to O(1) by using only two variables, as shown below.
Optimized Space Version of the Tabulation Approach
Instead of storing all values in an array, we can just keep the last two computed values:
public class TabulFibOptimized {
public static int tabulfib(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
// Use two variables to keep track of the last two Fibonacci numbers
int prev2 = 0;
int prev1 = 1;
for (int i = 2; i <= n; i++) {
int current = prev1 + prev2; // Calculate the current Fibonacci number
prev2 = prev1; // Update prev2 to be the previous value of prev1
prev1 = current; // Update prev1 to be the current value
}
// The last calculated value is the nth Fibonacci number
return prev1;
}
public static void main(String[] args) {
int n = 5;
System.out.println("The " + n + "th Fibonacci number using Optimized Tabulation is: " + tabulfib(n));
}
}
Space Complexity: O(1) because only two variables (
prev1andprev2) are used.Time Complexity remains O(n).
Summary
Tabulation builds solutions from smaller subproblems using an iterative approach.
It avoids recursion and is generally more efficient, especially for larger input sizes.
The Fibonacci problem is a great example where tabulation reduces time complexity from O(2^n) (recursive) to O(n) and can further reduce space complexity to O(1) with optimizations.
Tabulation is a powerful technique in DP, and mastering it will help solve many optimization and combinatorial problems efficiently!
Conclusion
Memoization (Top-Down) and Tabulation (Bottom-Up) are two powerful DP techniques.
Tabulation avoids the overhead of recursion and uses iteration, making it more efficient for large problems where recursion depth could cause stack overflow.
This example demonstrates how Tabulation is applied to the Fibonacci problem, reducing both time and space complexity compared to the naive recursive approach.
3. Seven Important Concepts in DP
Alright, let's dive into the seven key dynamic programming (DP) questions and why they are so essential. Think of these questions not as individual problems but as templates or patterns. Once you understand these patterns, you'll have a toolbox to solve many different types of problems. Imagine each of these problems as a building block that helps you solve a whole category of challenges in DP.
Why These 7 Questions?
1. Fibonacci Sequence
Pattern: Simple recurrence relation where each element depends on the previous two.
Subproblems:
Climbing Stairs: Similar to Fibonacci; at each step, you can either take one or two steps, so it follows a recurrence like
ways(n) = ways(n-1) + ways(n-2).Number Factors: Find the number of ways to express a number using a set of given numbers (e.g., 1, 3, and 4). It builds solutions based on smaller results, just like the Fibonacci pattern.
Min Jumps to Reach the End: Given an array of jumps, find the minimum number of jumps required to reach the end of the array.
Min Jumps with Cost: Similar to above but involves a cost associated with each jump.
House Thief: Find the maximum amount of money that can be stolen without stealing from two adjacent houses (similar recurrence as in Fibonacci).
Summary: These subproblems all build solutions incrementally, relying on previously computed values.
2. 0-1 Knapsack Problem
Pattern: Choose or exclude an item based on constraints (weight and value).
Subproblems:
Subset Sum: Check if any subset of numbers can sum up to a given value (similar structure where you either include or exclude numbers).
Equal Subset Sum Partition: Partition an array into two subsets with equal sums—essentially a variation of the subset sum problem.
Min Subset Sum Difference: Find the minimum difference between two subsets formed from the given set.
Count of Subset Sum: Count how many ways you can create a subset with a given sum.
Target Sum: Count the ways to assign
+and-to elements in the array to reach a target value.Mountain Ranges: Find the number of ways to arrange mountains such that no two ranges overlap.
Summary: All these subproblems involve making binary decisions (take or exclude), similar to the knapsack approach.
3. Unbounded Knapsack Problem
Pattern: Similar to 0-1 Knapsack but allows unlimited usage of each item.
Subproblems:
Rod Cutting: Maximize the profit by cutting a rod into pieces of various lengths.
Coin Change: Count the ways to make change for a value using unlimited coins.
Min Coin Change: Find the minimum number of coins needed to make a certain amount.
Max Ribbon Cut: Maximize the number of pieces a ribbon can be cut into, similar to rod cutting.
Summary: These subproblems involve unlimited choices and finding ways to maximize value using repeated options.
4. Longest Common Subsequence (LCS)
Pattern: Finding common elements between two sequences.
Subproblems:
Longest Common Substring: Similar to LCS but finds the longest contiguous common part.
Edit Distance: Count the minimum edits needed to convert one string to another.
Box Stacking: Find the tallest stack that can be formed using given boxes.
Longest Increasing Subsequence (LIS): Find the longest increasing sequence in an array.
Longest Bitonic Subsequence: Find the longest subsequence that first increases and then decreases.
Subsequence Pattern Matching: Count how many times a subsequence occurs in a sequence.
Summary: These subproblems often involve matching, transforming, or arranging sequences optimally.
5. Kadane’s Algorithm (Maximum Subarray)
Pattern: Finding the maximum sum subarray in an array.
Subproblems:
- Min Jumps with Cost: In this, you may use Kadane’s approach for solving the problem of finding the optimal sum with constraints (min jumps).
Summary: Kadane’s Algorithm focuses on efficiently finding maximum sums or paths using a DP approach, which extends to several array-based problems.
6. Catalan Numbers
Pattern: Counting recursive structures or arrangements.
Subproblems:
Number of Binary Search Trees (BSTs): Count how many unique BSTs can be formed with
nnodes.Valid Parentheses Combinations: Find all valid ways to arrange parentheses.
Disjoint Chords: Count ways to connect points on a circle without crossing chords.
Convex Polygons: Find ways to split a convex polygon into triangles.
Dyck Words: Count balanced sequences of parentheses.
Summary: Problems that require counting configurations of recursive structures, often related to combinatorial mathematics.
7. DP on Grids (2D Arrays)
Pattern: Pathfinding and optimizing movement in a grid.
Subproblems:
Min Cost Path: Find the minimum cost to traverse from the top-left to the bottom-right corner of a grid.
Unique Paths: Count the number of ways to reach the bottom-right corner of a grid.
Longest Increasing Path: Find the longest increasing path in a matrix.
Summary: Problems involving movement and pathfinding in 2D grids are foundational for solving a range of matrix and path-based challenges.
Why These 7 Questions Are Crucial
These questions are not just isolated problems. They represent patterns that can be reused in many other questions. For example:
The Fibonacci pattern can be applied to problems where each step or element depends on a few previous ones.
The Knapsack pattern helps you when you need to make choices based on constraints.
The Catalan number pattern appears in problems involving recursive structures or counting non-overlapping paths.
Once you understand these core problems, you can solve many others by applying the same techniques or patterns. It’s all about recognizing the structure of the problem and knowing which approach to use.
How Greedy Algorithms Fit In
In the Greedy Algorithms chapter, you saw the Activity Selection Problem, which is also a concept. It’s similar because it teaches a pattern for making the most optimal choice at each step, just like DP teaches you how to build optimal solutions from smaller pieces.
Summary
These 7 questions cover fundamental DP patterns that apply to many problems.
Understanding them deeply allows you to solve a wide range of other problems that follow similar structures.
It’s all about recognizing these core patterns and knowing how to apply them to different challenges.
Think of these questions as the blueprints. Once you understand the blueprint, you can build solutions for many other problems.
4. Climbing Stairs Problem (Recursion)
The Climbing Stairs problem is a classic dynamic programming problem that can be visualized as a variation of the Fibonacci sequence.
It is a variation of the Fibonacci sequence, where the goal is to calculate the number of ways a person can reach the nth stair if they can climb either 1 or 2 stairs at a time. Let's break this down step-by-step and visualize the process.
Problem Overview
The goal is to find the number of ways to reach the nth stair when:
- You can either take 1 stair at a time or 2 stairs at a time.
Visualization of the Problem
For ( n = 2 ):
Way 1: Climb to stair 1, then climb to stair 2.
Way 2: Climb directly to stair 2.
There are 2 ways to reach the 2nd stair.
For ( n = 3 ):
Way 1: Climb 1 by 1 (Stair 1 → Stair 2 → Stair 3).
Way 2: Climb 1 stair, then directly climb 2 stairs (Stair 1 → Stair 3).
Way 3: Climb 2 stairs, then 1 stair (Stair 2 → Stair 3).
So, there are 3 ways to reach the 3rd stair.
For ( n = 4 ):
Way 1: Climb 1 by 1 (Stair 1 → Stair 2 → Stair 3 → Stair 4).
Way 2: Climb 1 stair, 1 stair, and then 2 stairs (Stair 1 → Stair 2 → Stair 4).
Way 3: Climb 1 stair, 2 stairs, then 1 stair (Stair 1 → Stair 3 → Stair 4).
Way 4: Climb 2 stairs, then 1 stair, and then 1 stair (Stair 2 → Stair 3 → Stair 4).
Way 5: Climb 2 stairs at a time twice (Stair 2 → Stair 4).
So, there are 5 ways to reach the 4th stair.
Pattern Analysis
If we compare the ways for different values of ( n ):
For ( n = 3 ), there are 3 ways.
For ( n = 4 ), there are 5 ways.
Now, notice how the ways for ( n = 3 ) are also included in the ways for ( n = 4 ), but with an extra step (an additional 1 stair to reach ( n = 4 )). Similarly, the ways for ( n = 2 ) are also in ( n = 4 ), but with an additional 2 stairs to make up the difference.
This means that:
- Ways to reach ( n = 4 ) = Ways to reach ( n = 3 ) + Ways to reach ( n = 2 ).
So, if you are at:
( n - 1 ), you need just 1 more stair to reach ( n ).
( n - 2 ), you need 2 more stairs to reach ( n ).
Deriving the Relation
By analyzing this pattern:
Ways to reach ( n ) can be represented as:
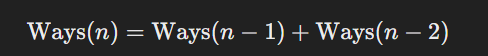
This is the same as the Fibonacci sequence, where each value is the sum of the two previous values.
Visualizing the Relation for n = 5:
Let’s take a more detailed look at n = 5:
If we already know the number of ways to reach n = 3 and n = 4:
Ways to reach
n = 5by taking 1 step fromn = 4(which has 5 ways):- We can use each of the 5 ways to reach
n = 4, and then just take 1 step.
- We can use each of the 5 ways to reach
Ways to reach
n = 5by taking 2 steps fromn = 3(which has 3 ways):- We can use each of the 3 ways to reach
n = 3, and then just take 2 steps.
- We can use each of the 3 ways to reach
Thus, the total number of ways to reach n = 5 is:
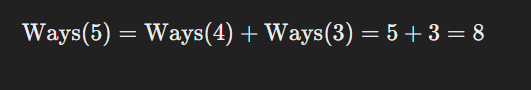
Pseudocode
The pseudocode for this problem using the above recurrence relation is as follows:
function countWays(n):
if n == 0:
return 1 // 1 way (we didn’t move)
if n < 0:
return 0 // No way (invalid)
return countWays(n-1) + countWays(n-2)
Base Cases Explained
( n = 0 ): There's only 1 way to stay at the start without moving.
( n < 0 ): There are no ways to move into negative steps, so return 0.
Why We Consider ( n < 0 )
If you have ( n = 1 ), the recurrence relation becomes:

We already know

For
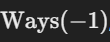
we return 0 as it’s an invalid move.
This ensures that our recurrence covers all scenarios without errors.
Here’s the code for the Climbing Stairs problem, which follows the recursive approach based on the Fibonacci pattern. I've added detailed comments to explain each part of the code and the problem statement.
/**
* Problem Statement:
* Given a staircase with 'n' steps, a person can climb either 1 step or 2 steps at a time.
* The task is to count the total number of ways to reach the nth step.
* This is a variation of the Fibonacci sequence because each step can be reached from either
* the previous step (n-1) or the step before that (n-2).
*
* Formula:
* Ways(n) = Ways(n-1) + Ways(n-2)
* Base Cases:
* - If n == 0, there's 1 way (you stay at the start without moving).
* - If n < 0, there's no way (negative steps are invalid).
*/
public class ClimbingStairs {
/**
* Method to count the number of ways to reach the nth step.
*
* @param n - the number of steps in the staircase
* @return the number of ways to reach the nth step
*/
public static int countWays(int n) {
// Base case: if n is 0, there is 1 way to reach (stay at the ground)
if (n == 0) {
return 1;
}
// Base case: if n is negative, no valid way exists (0 ways)
if (n < 0) {
return 0;
}
// Recursive step: sum of ways to reach (n-1) and (n-2) steps
return countWays(n - 1) + countWays(n - 2);
}
public static void main(String[] args) {
// Example: Finding the number of ways to reach the 5th step
int n = 5;
System.out.println("Number of ways to reach step " + n + ": " + countWays(n));
}
}
Explanation of the Code:
Base Cases:
If
n == 0, there's only one way to reach (stay on the ground). We return1.If
n < 0, there’s no valid way to climb negative steps, so we return0.
Recursive Formula:
We calculate the total ways by combining the number of ways to reach
(n-1)and(n-2)steps.This represents climbing either 1 step or 2 steps at a time.
Example Output:
If
n = 5, the output will be:Number of ways to reach step 5: 8.- This output corresponds to the 8 unique ways you can climb a staircase with 5 steps.
countWays(5)
/ \
countWays(4) countWays(3)
/ \ / \
countWays(3) countWays(2) countWays(2) countWays(1)
/ \ / \ / \ |
countWays(2) countWays(1) countWays(1) countWays(0)
/ \ | | |
countWays(1) countWays(0) 1 1
|
countWays(0)
This approach, however, is not efficient for larger n as it involves recalculating the same subproblems multiple times. We can optimize it using dynamic programming (e.g., memoization or tabulation).
This approach has a time complexity of O(2^n) because it recalculates subproblems multiple times, which is inefficient.
5. Climbing Stairs (Memoization DP)
Memoization Approach for Climbing Stairs
In the recursive approach, we see that certain calculations are repeated multiple times, leading to inefficiency and an exponential time complexity. Memoization helps solve this problem by storing the results of subproblems so that they are not recalculated.
Let's go through the memoization approach step by step:
Problem Visualization
Given
nstairs, a person can climb either 1 or 2 stairs at a time.We want to find the number of ways to reach the
nth stair.
Memoization Explanation
Memoization is a technique where we store the results of previous calculations to avoid redundant computations.
In our solution, we use an array
ways[]to store the number of ways to reach each stair.
Code Explanation
import java.util.Arrays;
public class ClimbingStairs {
public static int countWays(int n, int[] ways) {
// Base case: if n is 0, there is one way to stay at the ground
if (n == 0) {
return 1;
}
// If n is negative, there are no ways to reach this step
if (n < 0) {
return 0;
}
// If we have already calculated the number of ways for this step, return it
if (ways[n] != -1) { // Already calculated
return ways[n];
}
// Calculate and store the result for future use
ways[n] = countWays(n - 1, ways) + countWays(n - 2, ways);
return ways[n];
}
public static void main(String[] args) {
int n = 5;
int ways[] = new int[n + 1];
// Initialize the array with -1 to indicate uncalculated steps
Arrays.fill(ways, -1);
// Print the total ways to reach the nth stair
System.out.println(countWays(n, ways));
}
}
Why ways[] Array Size is n + 1
- The array
ways[]is of sizen + 1because we want to store results fromways[0]up toways[n]. This ensures that we have space to store the computed number of ways for each stair level from0ton.
Base Case (
n == 0):- If
nis 0, it means we are at the ground level, and there is only one way to stay there (by doing nothing).
- If
Negative Stairs (
n < 0):- If
nbecomes negative, it means we cannot reach this stair in any way, so the function returns 0.
- If
Memoization Check (
ways[n] != -1):- If
ways[n]is not-1, it means we have already calculated the number of ways to reach thenth stair, so we return it directly to save computation time.
- If
Recursive Calculation and Storage:
- We calculate
countWays(n - 1, ways) + countWays(n - 2, ways)to get the number of ways to reach thenth stair and store it inways[n]for future use.
- We calculate
Recursion Tree (Skewed Tree)
Memoization transforms the recursion tree into a skewed tree, where the nodes represent different values of
n:Initially, without memoization, the tree expands exponentially, with the same subproblems appearing multiple times.
With memoization, each unique subproblem (value of
n) is computed once and stored. If the function encounters a previously computed value, it retrieves the result from the array rather than making additional recursive calls.
Full Recursion Tree with Memoization for countWays(5)
countWays(5)
/ \
countWays(4) countWays(3)
/ \ / \
countWays(3) countWays(2) countWays(2) countWays(1)
/ \ / \ (cached) / \
countWays(2) countWays(1) countWays(1) countWays(0) countWays(0) countWays(-1)
/ \ / \ (cached) (cached) (cached) (cached)
countWays(1) countWays(0) countWays(0) countWays(-1)
/ \ (cached) (cached) (cached)
countWays(0) countWays(-1)
(cached) (cached)
Notes on the Tree:
Base Cases:
countWays(0)is called multiple times but returns1each time. Once it's computed, it’s stored and reused.countWays(-1)returns0each time it's called. This also happens multiple times but is reused after the first computation.
Memoized Calls:
- For example,
countWays(2)is called multiple times in different branches, but after it’s computed once, the memoized value is used in subsequent calls.
- For example,
Pruning the Tree:
- Once
countWays(2)and other values likecountWays(1)are stored in theways[]array, they do not expand further, significantly reducing the number of calls.
- Once
Time Complexity Analysis
Time Complexity:
O(n)- With memoization, each subproblem (
countWays(k)) is calculated only once, and we store the result in thewaysarray. Therefore, the function runs in linear time, making the time complexityO(n).
- With memoization, each subproblem (
Space Complexity:
O(n)- We use an array
ways[]of sizen + 1to store the results. Thus, the space complexity isO(n).
- We use an array
Memoization greatly optimizes the solution by transforming the problem from an exponential time complexity (O(2^n)) to linear time complexity (O(n)), making it efficient for larger values of n.
6. Climbing Stairs Variation
Let's dive into the Climbing Stairs Variation problem in detail, where the allowed steps are 1, 2, or 3 stairs at a time. This variation expands the solution beyond the basic Fibonacci-like sequence by including an extra step option.
Problem Statement
Given a staircase with n steps, you are allowed to climb either 1, 2, or 3 steps at a time. You need to find the number of distinct ways to reach the top of the staircase.
Visualizing the Problem
Let’s visualize the steps to understand how different combinations work:
For
n = 1:- There is only 1 way to climb (1 step).
For
n = 2:We have 2 ways:
Take two 1-steps:
(1 + 1)Take one 2-step:
(2)
For
n = 3:We have 4 ways:
(1 + 1 + 1)(1 + 2)(2 + 1)(3)
For
n = 4:We have 7 ways:
(1 + 1 + 1 + 1)(1 + 1 + 2)(1 + 2 + 1)(2 + 1 + 1)(2 + 2)(1 + 3)(3 + 1)
So, for n = 4, there are 7 ways. Notice how the number of ways increases as n increases, based on the possible combinations of steps.
Deriving the Formula
To find the number of ways to reach the nth stair, we can look at the last step taken:
If the last step taken was 1 stair, then we need the number of ways to reach
n - 1.If the last step taken was 2 stairs, then we need the number of ways to reach
n - 2.If the last step taken was 3 stairs, then we need the number of ways to reach
n - 3.
Thus, the relationship (recurrence relation) becomes:
[ \text{ways}(n) = \text{ways}(n-1) + \text{ways}(n-2) + \text{ways}(n-3) ]
This is similar to the Fibonacci sequence but extended to include the third previous step.
Code Explanation with Memoization
We use a dynamic programming approach with memoization to optimize the solution and avoid recalculating the same values multiple times. Here’s how it works:
import java.util.Arrays;
public class ClimbingStairs {
public static int countWays(int n, int[] ways) {
// Base case: if n is 0, there is one way to stay at the ground
if (n == 0) {
return 1;
}
// If n is negative, there are no ways to reach this step
if (n < 0) {
return 0;
}
// If we have already calculated the number of ways for this step, return it
if (ways[n] != -1) { // Already calculated
return ways[n];
}
// Calculate and store the result for future use
ways[n] = countWays(n - 1, ways) + countWays(n - 2, ways) + countWays(n - 3, ways);
return ways[n];
}
public static void main(String[] args) {
int n = 5;
int ways[] = new int[n + 1];
// Initialize the array with -1 to indicate uncalculated steps
Arrays.fill(ways, -1);
// Print the total ways to reach the nth stair
System.out.println(countWays(n, ways));
}
}
Explanation of the Code
Base Case:
If
n == 0, it means we are at the ground level, and there is only one way to stay there (do nothing), so we return1.If
n < 0, it means we have gone below the ground level, which is not possible, so we return0.
Memoization:
- We use an array
ways[]to store previously computed values. Ifways[n]is not-1, it means we have already calculated the number of ways to reach stepn, so we return that value directly.
- We use an array
Recurrence Relation:
- The line
ways[n] = countWays(n - 1, ways) + countWays(n - 2, ways) + countWays(n - 3, ways);calculates the total ways by summing the ways to reachn - 1,n - 2, andn - 3.
- The line
Output
If you run the program with n = 5, it outputs 13, indicating there are 13 ways to climb 5 stairs when you can take steps of 1, 2, or 3.
countWays(5)
├── countWays(4) (store result)
│ ├── countWays(3) (store result)
│ │ ├── countWays(2) (store result)
│ │ │ ├── countWays(1) (store result)
│ │ │ │ ├── countWays(0) => 1
│ │ │ │ └── countWays(-1) => 0
│ │ │ └── countWays(0) => 1 (already stored)
│ │ ├── countWays(1) => result already stored, use directly
│ │ └── countWays(0) => result already stored, use directly
│ ├── countWays(2) => result already stored, use directly
│ └── countWays(1) => result already stored, use directly
├── countWays(3) => result already stored, use directly
└── countWays(2) => result already stored, use directly
Time Complexity
With memoization, the time complexity of the code is reduced to O(n) because each state (from 0 to n) is computed only once.
This approach ensures that we don't recompute values unnecessarily, making it efficient even for larger n.
7. Climbing Stairs (Tabulation DP)
Using the bottom-up approach, we start from the smallest subproblem and build the solution iteratively.
Tabulation Approach
The idea behind tabulation is to build a solution iteratively from the base case, storing the results in a table (array) to avoid recalculating the same subproblems. Here's how we proceed:
Step 1: Create the Table and Initialize It
We create a 1D array called
dpbecause we only have one changing variable: the stair number (n).dp[i]represents the number of ways to reach thei-th stair.Base Case Initialization:
dp[0] = 1: There's only one way to stay at the ground level (not climbing any stairs).For values where
i < 0, it's implicitly 0 because there's no way to reach negative stairs.
Step 2: Understand the Meaning of Each Index
Each index in the
dparray corresponds to the number of ways to reach that specific stair.For example,
dp[3]will tell us how many ways we can reach the 3rd stair using steps of 1 or 2.
Step 3: Fill the Table in a Bottom-Up Manner
We start filling from
i = 1toi = n.For each
i:If
i == 1, the number of ways is simplydp[i] = dp[i-1]because we can only take one step to reach stair 1.For
i >= 2,dp[i] = dp[i-1] + dp[i-2]because:- We can reach stair
ifrom stairi-1(1 step) or stairi-2(2 steps).
- We can reach stair
Updated Code with Comments
import java.util.Arrays;
public class ClimbingStair {
public static int countWaysTab(int n) {
// Create a dp array to store the number of ways to reach each stair
int dp[] = new int[n + 1];
// Base case: There's 1 way to stay at the ground (0th stair)
dp[0] = 1;
// Iterate from stair 1 to stair n
for (int i = 1; i <= n; i++) {
// If we're at the 1st stair, we can only come from the 0th stair
if (i == 1) {
dp[i] = dp[i - 1];
} else {
// Otherwise, we can come from either the previous stair (i-1) or two stairs back (i-2)
dp[i] = dp[i - 1] + dp[i - 2];
}
}
// Return the number of ways to reach the nth stair
return dp[n];
}
public static void main(String[] args) {
int n = 5; // Number of stairs
System.out.println(countWaysTab(n)); // Output the number of ways to reach the nth stair
}
}
Explanation of the Code
Initialization:
dp[0]is set to 1 because there's one way to stay at the ground (no movement).Filling the dp array:
For
i = 1, we setdp[1] = dp[0]because we can only step up one stair from the ground.For all other values (
i >= 2),dp[i]is the sum of the ways to get to the previous stair (dp[i-1]) and the ways to get to the stair two steps before (dp[i-2]).
Output
For n = 5, the output is:
8
This indicates there are 8 ways to reach the 5th stair using steps of 1 or 2.
Here's how the array fills up visually for n = 5:
Index (i) | dp[i] | Explanation |
| 0 | 1 | Base case: staying on the ground, 1 way. |
| 1 | 1 | One way to reach the 1st stair (1 step). |
| 2 | 2 | Two ways: (1+1) or (2). |
| 3 | 3 | Three ways: (1+1+1), (1+2), or (2+1). |
| 4 | 5 | Five ways: (1+1+1+1), (1+1+2), (1+2+1), (2+1+1), (2+2). |
| 5 | 8 | Eight ways: combinations of previous steps. |
This table shows how we build up the number of ways step by step using previously computed values.
Recap of the Tabulation Process
Table Creation: We create a 1D array (
dp[]) because only one variable (irepresenting the stair number) is changing.Initialization: We set
dp[0] = 1because there's only one way to stay on the ground.Filling the Array:
We fill the array from the smallest index (
i = 1) to the largest (i = n).We ensure that each step relies only on previously computed values (
i-1andi-2).
This approach ensures the solution is computed in O(n) time with O(n) space, avoiding the exponential time complexity of the recursive approach.
Here, we fill up the dp array from index 0 to n, which has a time complexity of O(n) and space complexity of O(n).
Conclusion of Chapter 41: Dynamic Programming (DP) - Part 1
Dynamic Programming (DP) provides a structured approach to solving complex problems by leveraging previously computed results, ensuring efficiency and optimization. By breaking down problems into smaller overlapping subproblems and using either memoization (top-down) or tabulation (bottom-up), we can drastically reduce computation time compared to naive approaches.
Key takeaways include:
Memoization: Caches results of function calls, avoiding redundant computations in recursive solutions.
Tabulation: Uses an iterative approach to build solutions from the smallest subproblems up to the desired result, often represented in a DP table (array).
DP works best when problems have overlapping subproblems and optimal substructure, such as in the Climbing Stairs problem, where the number of ways to reach a stair is derived from previous steps.
Understanding these principles lays the foundation for solving a wide range of optimization and counting problems efficiently.
Related Posts
Related Series
Connect With Me
Feel free to connect and follow me on:
Stay tuned for more updates on my blog series!
Your feedback and engagement are invaluable. Feel free to reach out with questions, comments, or suggestions. Happy coding!
Rohit Gawande
Full Stack Java Developer | Blogger | Coding Enthusiast
Subscribe to my newsletter
Read articles from Rohit Gawande directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
Rohit Gawande
Rohit Gawande
🚀 Tech Enthusiast | Full Stack Developer | System Design Explorer 💻 Passionate About Building Scalable Solutions and Sharing Knowledge Hi, I’m Rohit Gawande! 👋I am a Full Stack Java Developer with a deep interest in System Design, Data Structures & Algorithms, and building modern web applications. My goal is to empower developers with practical knowledge, best practices, and insights from real-world experiences. What I’m Currently Doing 🔹 Writing an in-depth System Design Series to help developers master complex design concepts.🔹 Sharing insights and projects from my journey in Full Stack Java Development, DSA in Java (Alpha Plus Course), and Full Stack Web Development.🔹 Exploring advanced Java concepts and modern web technologies. What You Can Expect Here ✨ Detailed technical blogs with examples, diagrams, and real-world use cases.✨ Practical guides on Java, System Design, and Full Stack Development.✨ Community-driven discussions to learn and grow together. Let’s Connect! 🌐 GitHub – Explore my projects and contributions.💼 LinkedIn – Connect for opportunities and collaborations.🏆 LeetCode – Check out my problem-solving journey. 💡 "Learning is a journey, not a destination. Let’s grow together!" Feel free to customize or add more based on your preferences! 😊