Hello,
Lets continue our discussion in some points that will help you to understand better

1. Problem Statement :-
   Given an array of integers nums_array and an integer k, we are tasked with counting the number of continuous subarrays whose sum equals k. For example, if we have the array nums_array = [1, 1, 1] and k=2, the output should be 2 since the subarrays [1, 1] and [1, 1] both sum to 2.

2. Hint :-

Suppose

1. We have coins of 1, 2, 3, …., n.
   2) This coins are put in a single line and we need to start from left and go towards right. Now stick all the coins with glue.
   3) Now we want a stack of coins where sum of all coins is k. Now we can check, if we can cut the coins from the left side of the stacked coins such that the stacked coin sum is k. It is possible to cut 2 coins if and only if they are sticked by glue, means if we will stick the coins 4 and 5 then we get a stacked coin of 9.
   4) We can cut the 9 as (4, 5) and not in any other.
   5) So we need to check if we can cut some stack from the start and the remaining coins must sum to k.
   6) This Stacking of coins is pre-sum Method.

What is Pre-Sum of Arrays

Example:

Given an array: arr = [2, 4, 6, 8, 10]

Step 1: Build the prefix sum array (presum):
- presum[0] = 2
- presum[1] = 2 + 4 = 6
- presum[2] = 6 + 6 = 12
- presum[3] = 12 + 8 = 20
- presum[4] = 20 + 10 = 30

So, presum = [2, 6, 12, 20, 30]

Step 2:To find the sum of elements from index 1 to 3 (i.e., 4 + 6 + 8):
presum[3]-presum[0]

This method reduces the time complexity for range sum queries.

1. Lets understand the Solution to the Problem Using presum and hashmaps(unordered maps) Finding Subarray Sums Equal to K: A Simple Explanation

Imagine you have an array of numbers representing the scores of your favorite games:

Array: [1, 2, 3, 4, 5]

And you want to find how many subarrays (continuous sections) of this array add up to a specific number k. Let’s say k=5.

Step-by-Step Approach

1. What is a Subarray? Let the Array be array = [1, 2, 3, 2, 4]
   A subarray is just a part of the array you can take without skipping any elements. For example, [1, 2], [2, 3, 2], or the whole array [1, 2, 3, 2, 4] are all subarrays.

2. Next task is Finding Subarrays that Sum to k:

You go through the array and keep adding the numbers(like stacking the coins as discussed above):

• Start at the first element:

• 1 (total = 1)

• 1+2 (total = 3)

• 1+2+3 (total = 6) — too much!

• Now, let’s check from the second element:

• 2(total = 2)

• 2+3 (total = 5) — perfect!

• 2+3+2 (total = 7) — too much!

• Now, from the third element:

• 3(total = 3)

• 3+2 (total = 5) — perfect!

• Finally, from the fourth element:

• 2 (total = 2)

• 2+4(total = 6) — too much!

• And lastly, the fifth element:

• 4 (total = 4) — not enough!

1. Counting the Matches:

• We found two subarrays that add up to k=5:

• [2, 3]

• [3, 2]

• So, the total count of subarrays that sum to k is 2.

2. Lets Get to the code and lets understand the solution

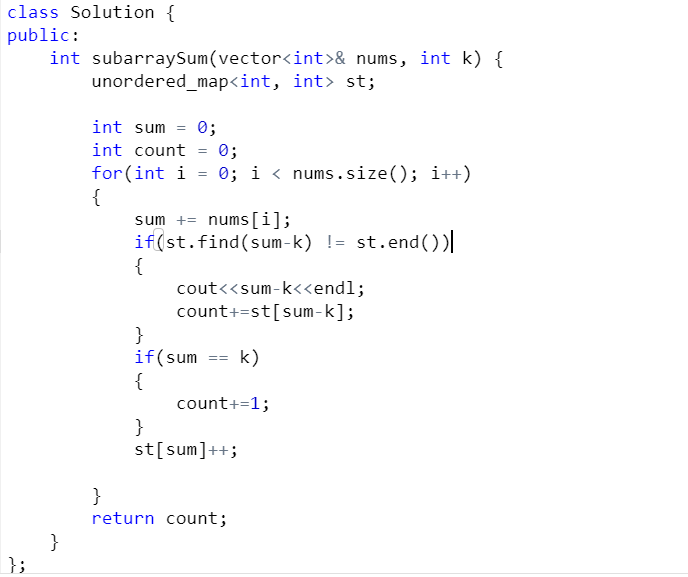
Complexity Analysis

• Time Complexity: The algorithm runs in O(n) time, where n is the length of the input array, as we make a single pass through the array.

• Space Complexity: The space complexity is O(n) in the worst case due to the storage of prefix sums in the hash map.

Code Explaination :

How It Works:

1. Prefix Sum:

• As we iterate through the array, we maintain a running sum (sum) that stores the cumulative sum of elements up to the current index.

• The idea is to check if there’s a previous prefix sum such that the difference between the current sum and k has been seen before.

2. Hashmap:

• The hashmap (st) stores the frequency of each prefix sum we encounter.

• Key: The prefix sum at any point.

• Value: The number of times this sum has occurred.

3. Sum — k exists

If sum — k exists in the hashmap, it means there is a subarray whose sum is exactly k.

1. Key Conditions:

• If sum == k, it means a subarray from the start sums up to k, so we increment the count.

• If sum — k exists in the hashmap, it means a subarray between some earlier point and the current index sums to k, so we add the count of occurrences of sum — k to the total count.

Increment Hashmap:

• After checking, we update the hashmap to include the current sum (sum), which helps in tracking future subarrays.

Why Hashmaps ?

• The hashmap efficiently stores and retrieves the frequency of prefix sums, allowing us to check in constant time whether the required subarray (sum — k) has been seen before. Without the hashmap, we would need to recheck all previous sums, which would make the algorithm slower.

Example:

For nums= [1, 2, 3] and k = 3:

• Step 1: sum = 1→ not found sum-k → st = {1:1}

• Step 2: sum = 3→ found sum-k = 0→ count += 1 → st : {1:1, 3:1}

• Step 3: sum = 6→ found sum-k = 3→ count += 1 → st = {1:1, 3:1, 6:1}

Answer: 2 subarrays with sum = k([1, 2] and [3]).

Why Do We Need a Map Instead of a Set?
In this problem, the goal is to count the number of subarrays that sum to a given target k. To achieve this efficiently, we use a hashmap (unordered_map) rather than a set because of the need to track frequencies of prefix sums.

A set can only store unique sums, so it wouldn’t track multiple subarrays that sum to the target k. In contrast, a map stores the prefix sums along with their frequencies, allowing us to correctly count all subarrays that satisfy the condition, even if the same sum appears more than once.

The map helps handle cases where multiple subarrays could sum to k by keeping track of how many times each prefix sum has occurred.