Solving the “Number of Islands” Problem in JavaScript

Photo by Cyrus Crossan on Unsplash

Algorithmic problem-solving is central to coding interviews, especially for software engineering roles at major tech companies like Google, Facebook, and Amazon. While these challenges might not fully reflect day-to-day engineering work or predict long-term success, preparing for them is critical.

Consistent practice, recognizing common problem-solving patterns, and being able to explain the efficiency and trade-offs of your solutions are key to landing a job offer in a competitive hiring environment or gaining admissions to a reputable coding bootcamp. Demonstrating a clear understanding of time and space complexity and articulating your approach effectively will help you excel in these assessments.

The “Number of Islands” Problem on LeetCode in JavaScript

The Number of Islands problem on Leetcode asks you to determine the number of distinct islands in a 2D grid, where each island is represented by connected groups of “1”s (land), and “0”s represent water. Two pieces of land are connected if they are adjacent either horizontally or vertically (i.e. diagonal adjacency doesn’t count). The toy problem requires you to count how many separate islands exist in this grid.

Problem Description

Given an m x n 2D binary grid which represents a map of '1's (land) and '0's (water), return the number of islands.

An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.

Solving the Number of Islands Problem Using Depth First Search (DFS)

Since we’ll need to check every cell in the matrix while also comparing the relative positions of cells (i.e. if a land cell adjacent to another land cell), using graph traversal will come in handy. Every cell has adjacent cells, and those cells have their own adjacent cells, so designing this algorithm around a graph structure will be optimal. I find DFS easier to conceptualize and more intuitive than Breadth First Search (BFS), so we’ll begin there.

Building a Mental Model for the Depth First Search Solution

Although graph traversal can be a little intimidating at first, having a strong mental model can make things a lot easier. I like to visualize the algorithm with diagrams.

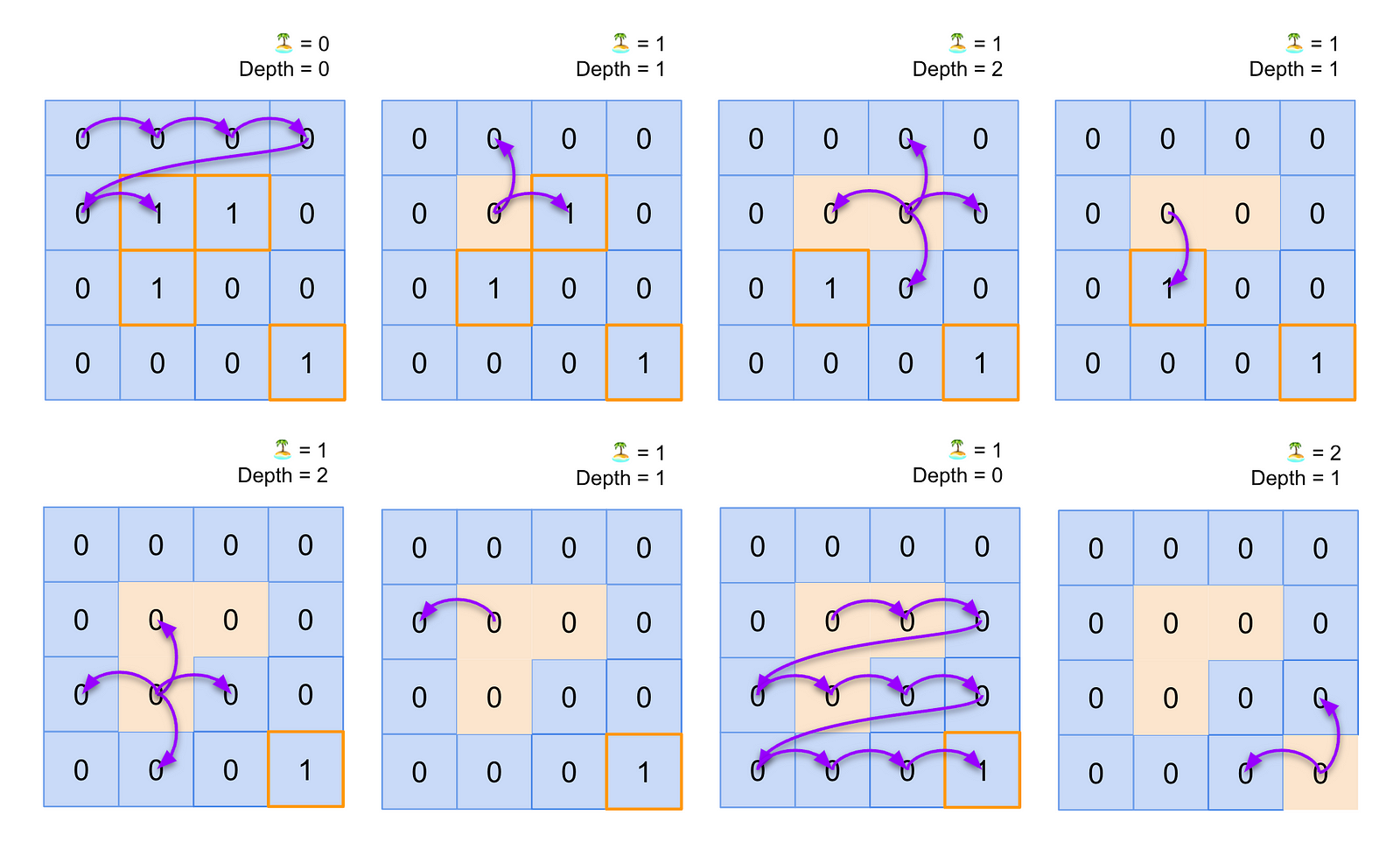
A diagram illustrating a depth-first search solution to the Number of Islands problem

In our DFS implementation, we’ll iterate through each row of the matrix until we find a land cell — or a cell with a value of “1”. We’ll then increment our island count by one and change that cell’s value to “0” to indicate that we’ve already checked it. Then, we’ll recursively check that cell’s adjacent cells — up, down, left, and right — to see if those cells contain land. We’ll continue to recursively check for land until all directions lead to water.

From there, we’ll continue to iterate through the matrix from where we left off, checking for land along the way. We’ll use the same steps as before when we encounter land, and the algorithm will terminate once we have no cells left to check.

A JavaScript Implementation of Depth First Solution to the Number of Islands Problem

function calculateIsWaterCell(grid, rowIndex, columnIndex) {
  const rowCount = grid.length;
  const columnCount = grid[0].length;
  const isRowOutOfBounds = rowIndex < 0 || rowIndex >= rowCount;
  const isColumnOutOfBounds =
    columnIndex < 0 ||
    columnIndex >= columnCount;
  const isWaterCell =
    isRowOutOfBounds ||
    isColumnOutOfBounds ||
    grid[rowIndex][columnIndex] === '0';

  return isWaterCell;
}

function searchGridForLand(grid, rowIndex, columnIndex) {
  const isWaterCell = calculateIsWaterCell(grid, rowIndex, columnIndex);

  if (!isWaterCell) {
    grid[rowIndex][columnIndex] = '0';

    searchGridForLand(grid, rowIndex - 1, columnIndex);
    searchGridForLand(grid, rowIndex + 1, columnIndex);
    searchGridForLand(grid, rowIndex, columnIndex - 1);
    searchGridForLand(grid, rowIndex, columnIndex + 1);
  }
}

function countIslands(grid) {
  let islandCount = 0;

  if (grid.length > 0) {
    for (let i = 0; i < grid.length; i++) {
      for (let j = 0; j < grid[0].length; j++) {
        const cell = grid[i][j];
        if (cell === '1') {
          islandCount += 1;
          searchGridForLand(grid, i, j);
        }
      }
    }
  }

  return islandCount;
}

Once our mental model is solidified, codifying this algorithm becomes much easier. For clarity, I’ve abstracted out the algorithm logic into three sections:

1. calculateIsWaterCell
   This function is solely focused on determining whether or not a cell is a water cell. Most of the logic is concerned with checking if the cell is out of bounds (outside the body of the grid) because the problem states that the grid itself is surrounded by water. The function also checks if the current cell’s value is “0”. One could make an argument that this function should not have knowledge of the grid at all, and the function should be further abstracted. I generally agree with that notion, however, readability is important in a tutorial and excessive abstraction works against that goal.

2. searchGridForLand
   Again, we are mixing concerns about grids and what constitutes a water cell here, but this is done for clarity. That aside, we’re primarily focused on recursion with this function. The logic checks for land, and if the current cell is land, it will toggle that cell to be water to indicate we’ve already traversed it and then it will recursively check all four directions for adjacent land. Subsequently, if any of those recursive calls also find land, they will continue down the graph with more recursive calls of searchGridForLand.

3. countIslands
   This is the entry point to the algorithm, and it is responsible for counting islands and iterating through the cell matrix. When we do encounter land, we’ll increment our islandCount variable and then recursively check for adjacent land cells.

Time and Space Complexity

• Time Complexity The time complexity of this solution is considered O(m × n), where m is the number of rows and n is the number of columns in the grid. For clarity, you can think of this complexity as O(n²) because m and n are effectively equal as they both approach infinity. In the worst case, we may need to visit all cells, and each cell is visited only once, so the complexity is proportional to the number of cells.

• Space Complexity This algorithm is considered to have O(m × n) space complexity. Due to the recursion stack used by DFS — particularly if the grid is filled with land cells forming a single large island — the stack depth could equal the total number of cells.

Solving the Number of Islands Problem Using Breadth First Search (BFS)

Breadth First Search (BFS) is an important concept to learn and can be a useful tool in certain situations, but I find it more complicated to understand and unnecessary in most cases. Nonetheless, we’ll take this opportunity to show you the difference and examine its efficiency.

Building a Mental Model for the Breadth First Search Solution

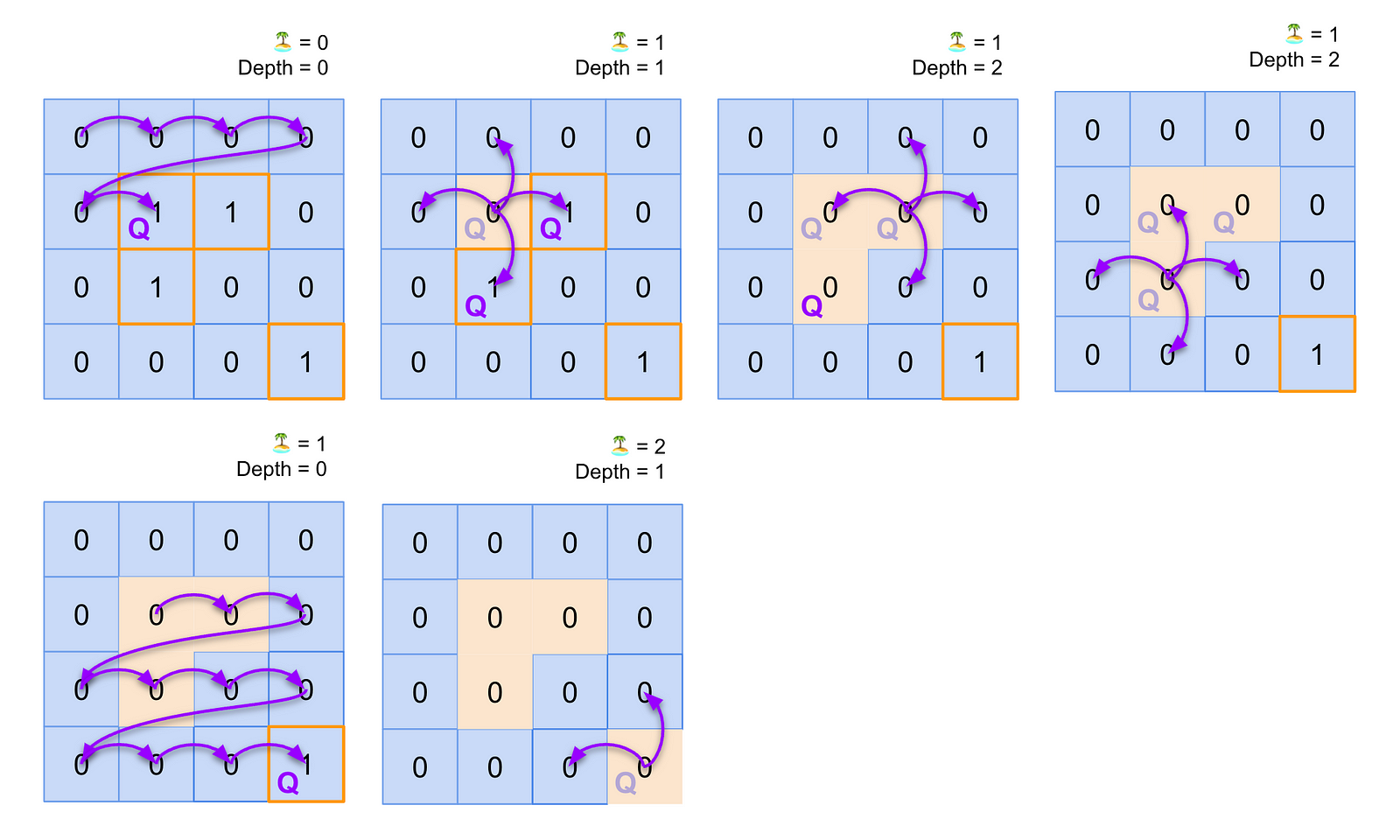
A diagram illustrating a breadth-first search solution to the Number of Islands problem

Similarly to the DFS implementation, we’ll start by iterating through each row of the matrix until we find a land cell (“1”). We also increment our island count at this level, but you’ll notice we check the entire “level” — also sometimes “layer” or “depth” — and we enqueue each of those cells before we dive deeper into them to check their descendants for land.

A JavaScript Implementation of Breadth First Solution to the Number of Islands Problem

function calculateIsWaterCell(grid, rowIndex, columnIndex) {
    const rowCount = grid.length;
    const columnCount = grid[0].length;
    const isRowOutOfBounds = rowIndex < 0 || rowIndex >= rowCount;
    const isColumnOutOfBounds = columnIndex < 0 || columnIndex >= columnCount;
    const isCellWater = isRowOutOfBounds || isColumnOutOfBounds || grid[rowIndex][columnIndex] === '0';

    return isCellWater;
}

function searchGridForLand(grid, rowIndex, columnIndex) {
    const queue = [[rowIndex, columnIndex]];
    grid[rowIndex][columnIndex] = '0';

    while (queue.length > 0) {
        const [i, j] = queue.shift();
        const newCellsToCheck = [
            [i - 1, j],
            [i + 1, j],
            [i, j - 1],
            [i, j + 1]
        ];

        for (let [newI, newJ] of newCellsToCheck) {
            const isCellWater = calculateIsWaterCell(grid, newI, newJ);

            if (!isCellWater) {
                queue.push([newI, newJ]);
                grid[newI][newJ] = '0';
            }
        }
    }
}

function countIslands(grid) {
    let islandCount = 0;

    if (grid.length > 0) {
        for (let i = 0; i < grid.length; i++) {
            for (let j = 0; j < grid[0].length; j++) {
                const cell = grid[i][j];
                if (cell === '1') {
                    islandCount += 1;
                    searchGridForLand(grid, i, j);
                }
            }
        }
    }

    return islandCount;
}

You’ll notice in this implementation that the code for the countIslands and calculateIsWaterCell functions are identical to their respective DFS versions. That is because I purposefully separated concerns and abstracted out the core responsibilities into isolated functions. Now, it makes it easier to swap out the graph traversal logic — the code body inside of the searchGridForLand function — and for others to easily read and digest the algorithm.

Let’s break down the logic piece by piece:

1. First, we create a bare-bones queue and initialize it with the indices of the current cell we’re examining. A queue is a linear data structure that follows the First-In-First-Out (FIFO) principle — where elements are added at the back (enqueue) and removed from the front (dequeue) — ensuring that the first element inserted is the first one to be processed. We also mark this cell as already traversed by setting its value to “0” like we did in our DFS implementation.

2. Next we loop through the contents of the queue, check all adjacent cells for land, and enqueue any new land cells we find along the way. Since our logic is constructed using a while loop, we can keep enqueuing more cells to check and the algorithm will continue until the queue is not empty. In this portion of the function, we also dequeue each cell as we go along so that are while loop knows when to conclude and we also mark visited cells as water like before.

Time and Space Complexity

• Time Complexity Similarly to the DFS solution, the time complexity of this solution is considered O(m × n), where m is the number of rows and n is the number of columns in the grid. This is because we still need to iterate through all of the cells, and there isn’t any reason to believe that checking each level completely first before examining their descendant nodes would be any faster.

• Space Complexity This algorithm is considered to have O(m × n) space complexity. Due to the recursion stack used by DFS — particularly if the grid is filled with land cells forming a single large island — the stack depth could equal the total number of cells.

Edge Cases to Consider

1. Empty Grid If the grid is empty, the number of islands should be 0. This is handled by checking if the grid length is 0 at the start.

2. All Water If the grid contains no “1”s, the function should return 0 since there are no islands to count.

3. All Land If the grid consists entirely of land, the algorithm should handle this case by correctly counting either one island.

Variants of the Number of Islands Problem

1. Number of Closed Islands A close variant of the Number of Islands problem is where an island is only counted if it is completely surrounded by water on all four sides. This is an awesome variant to practice because it involves using the returned values from the recursive calls.

2. Number of Distinct Islands Another variant where islands that have the same shape (regardless of their orientation) are considered identical and counted only once.

When To Use Depth First Search Versus Breadth First Search

Choosing between DFS and BFS depends on the problem at hand and the structure of the graph or tree you are traversing. DFS is well-suited for problems where you need to explore all possible paths or “dig deep” into one branch before backtracking. It’s commonly used in scenarios like finding connected components in a graph, solving maze or puzzle problems, or performing topological sorting on a Directed Acyclic Graph (DAG). A real-world example is web crawling, where DFS can explore a website’s structure deeply before moving on to other pages.

On the other hand, BFS excels when the shortest path or minimum number of steps is important. BFS explores nodes level by level, making it ideal for shortest path problems in unweighted graphs, such as finding the minimum distance between two points in a grid or map. It’s often used in real-world scenarios like GPS navigation systems, where you want the shortest route to a destination, or in social network analysis to find the shortest connection between people. In general, use BFS when proximity is important and DFS when deep exploration or pathfinding is needed.

Conclusion

This problem is an excellent introduction to graph traversal techniques like DFS and BFS, often used in interviews to test a candidate’s understanding of recursive algorithms and grid-based problem-solving.

Let me know in the comments what you liked or disliked with this walkthrough, and if you enjoyed these explanations and diagrams, check out some more posts where I break down toy problems:

• Coding Interviews: Solving the “Palindrome Permutation” Problem in JavaScript

• Coding Interviews: Solving the “Rotate a Matrix” Problem in JavaScript

• Coding Interviews: Solving the “Reverse a Linked List in Place” Problem in JavaScript

Or if you’re looking to learn more about data structures, check out these:

• How to Build a Hash Table in JavaScript

• How to Build a Binary Search Tree in JavaScript

• How to Build a Linked List in JavaScript