Quick Sort Simplified: The Ultimate Beginner's Guide to Fast Sorting
 Keerthi Ravilla Subramanyam
Keerthi Ravilla SubramanyamTable of contents

In our previous articles, we've explored sorting algorithms like Bubble Sort, Selection Sort, Insertion Sort, and Merge Sort. Now, let's dive into Quick Sort, another popular and efficient sorting algorithm widely used in practice.
What is Quick Sort?
Quick Sort is a divide-and-conquer algorithm that sorts an array by partitioning it into smaller sub-arrays. It selects a 'pivot' element and reorders the array such that all elements less than the pivot come before it, and all elements greater than the pivot come after it. The process is recursively applied to the sub-arrays.
Key Concepts of Quick Sort
Pivot Selection: The algorithm selects a pivot element (can be the first, last, or a random element).
Partitioning: Rearranging the array so that elements smaller than the pivot move to the left, and elements larger move to the right.
Recursion: Quick Sort then recursively applies the same steps to the sub-arrays on both sides of the pivot.\
Ways to Choose the Pivot in Quick Sort
Choosing the right pivot is key to the efficiency of Quick Sort. There are several common strategies to select the pivot:
First Element: Select the first element in the array as the pivot.
Advantage: Simple and quick.
Disadvantage: Can lead to poor performance on already sorted or nearly sorted arrays.
Last Element: Select the last element as the pivot.
Advantage: Easy to implement, often used in introductory explanations.
Disadvantage: Like the first element, it can cause inefficient sorting in certain cases.
Random Element: Select a random element from the array.
Advantage: More likely to avoid worst-case performance.
Disadvantage: Requires random number generation, slightly more complex.
Median of Three: Select the median of the first, middle, and last elements as the pivot.
Advantage: A good balance, reduces the chances of hitting worst-case performance.
Disadvantage: Slightly more computation needed to determine the median.
For simplicity, we'll use the last element as the pivot in the following explanation.
Quick Sort Algorithm in Action
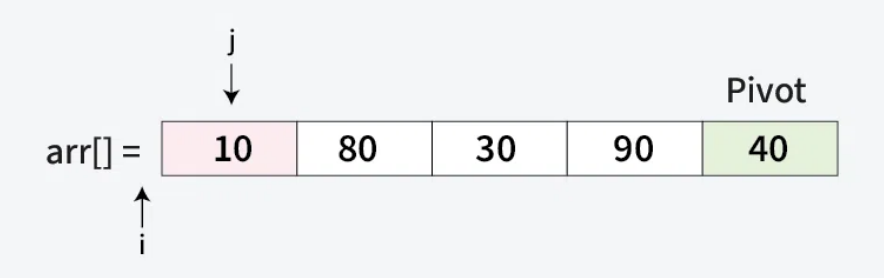
Let’s sort the array [10, 80, 30, 90, 40] using Quick Sort, with the last element as the pivot. Here is step-by-step explanation of Quick Sort Using the First Element as Pivot.
Step 1: Choose the Pivot
Pivot: The last element,
40.
Step 2: Partition the Array
We need to rearrange the array so that all elements smaller than 40 are to the left, and all elements larger than 40 are to the right of
40.Comparisons:
10 < 40: Keep10on the left.80 > 40: Ignore it for now.30 < 40: Swap30with80.Array after swapping:
[10, 30, 80, 90, 40]
Now, swap the pivot
40with80to place the pivot in its correct position.
Array after partition:
[10, 30, 40, 90, 80]The pivot
40is now correctly placed, and we have two sub-arrays:[10, 30]on the left and[90, 80]on the right.
Step 3: Recursively Sort the Left Sub-array [10, 30]
Pivot: The last element,
30.Comparisons:
10 < 30: Keep10on the left.Since
30is already in its correct position, the array is already sorted.
- Array after partition:
[10, 30]
No further sorting is needed for this sub-array.
Step 4: Recursively Sort the Right Sub-array [90, 80]
Pivot: The last element,
80.Comparisons:
90 > 80: Swap90with80.Array after partition:
[80, 90]
The sub-array [80, 90] is now sorted.
step 4: Final Sorted Array
After sorting all the sub-arrays, the fully sorted array becomes:
- Sorted array:
[10, 30, 40, 80, 90]

Comparision of Insertion and Quick sorts
Oh, wait... did you notice the similarity? At first glance, Quick Sort and Insertion Sort might seem alike because both involve comparing elements and rearranging them in the correct order. However, their underlying methods and strategies are quite different. Here's why they may appear similar but are actually distinct:
| Aspect | Quick Sort | Insertion Sort |
| Sorting Strategy | Divide-and-conquer using a pivot to partition the array into smaller sub-arrays. | Incrementally sorts the array one element at a time by inserting elements into their correct position. |
| Approach | Recursive algorithm. | Iterative algorithm. |
| Pivot Selection | Chooses a pivot (first, last, random, or median of three) to partition the array. | No pivot, focuses on inserting each element into the sorted portion of the array. |
| Time Complexity (Best Case) | O(n log n) | O(n) |
| Time Complexity (Average Case) | O(n log n) | O(n^2) |
| Time Complexity (Worst Case) | O(n^2) (when the array is already sorted or nearly sorted with poor pivot selection) | O(n^2) (especially with reverse sorted data) |
| Space Complexity | O( log n) due to recursion stack. | O(1) in-place sorting, no extra memory required. |
| Best Use Case | Large datasets, typically unsorted or random data. | Small datasets, or nearly sorted data. |
| Sorting Mechanism | Partitions the array around the pivot and recursively sorts sub-arrays. | Moves elements to the left by shifting them to insert the new element in its proper position. |
| Efficiency | Generally faster on large datasets due to O(n log n) average time complexity. | Slower for large datasets, but faster for small or nearly sorted arrays. |
| Stability | Not a stable sort (can be made stable with modifications). | Stable sort (preserves the relative order of equal elements). |
| Recursion | Yes, recursive algorithm. | No, typically iterative. |
| Swapping/Insertion | Uses swapping to move elements across partitions. | Uses shifting to insert elements into their correct position. |
| Implementation Complexity | More complex to implement due to partitioning and recursion. | Easier to implement, with straightforward element comparisons and shifts. |
Pseudocode for Quick Sort
Here’s a simple pseudocode for Quick Sort:
function quickSort(arr, low, high):
if low < high:
pivotIndex = partition(arr, low, high)
quickSort(arr, low, pivotIndex - 1) // Sort left part
quickSort(arr, pivotIndex + 1, high) // Sort right part
function partition(arr, low, high):
pivot = arr[high]
i = low - 1
for j = low to high - 1:
if arr[j] < pivot:
i = i + 1
swap arr[i] with arr[j]
swap arr[i + 1] with arr[high]
return (i + 1)
Python Code for Quick Sort
Let’s translate the pseudocode into Python:
# Quick Sort in Python
def quick_sort(arr, low, high):
if low < high:
pi = partition(arr, low, high)
quick_sort(arr, low, pi - 1) # Recursively sort the left part
quick_sort(arr, pi + 1, high) # Recursively sort the right part
def partition(arr, low, high):
pivot = arr[high] # Choosing the last element as the pivot
i = low - 1 # Index of smaller element
for j in range(low, high):
if arr[j] < pivot:
i = i + 1
arr[i], arr[j] = arr[j], arr[i] # Swap if current element is smaller
arr[i + 1], arr[high] = arr[high], arr[i + 1] # Move pivot to correct position
return i + 1
# Example usage
arr = [8, 3, 1, 7, 0, 10, 2]
n = len(arr)
quick_sort(arr, 0, n - 1)
print("Sorted array is:", arr)
Explanation:
quick_sort: The main function that recursively sorts the array by calling the
partitionfunction.partition: Divides the array around a pivot and rearranges elements.
When you run the above code, the output will be:
Sorted array is: [0, 1, 2, 3, 7, 8, 10]
Advantages of Quick Sort
Efficiency: Quick Sort is much faster than simpler algorithms like Bubble Sort, Insertion Sort, and even Selection Sort in most cases.
In-place Sorting: It doesn’t require extra space for another array, making it more space-efficient than Merge Sort.
Divide and Conquer: This approach simplifies the problem by breaking it into smaller sub-problems.
Disadvantages of Quick Sort
Worst-case Time Complexity: If the pivot is poorly chosen (e.g., always the smallest or largest element), the performance degrades to O(n²).
Unstable: Quick Sort is not a stable sorting algorithm, meaning it doesn’t maintain the relative order of equal elements.
Recursion: For large datasets, excessive recursion could lead to stack overflow issues.
Time Complexity of Quick Sort
Best Case: O(n log n) – This happens when the pivot divides the array into two nearly equal parts.
Average Case: O(n log n) – Even for randomly distributed inputs, Quick Sort performs efficiently.
Worst Case: O(n²) – This occurs when the pivot is poorly chosen, leading to unbalanced partitions (e.g., when the array is already sorted).
Conclusion
Quick Sort is one of the most widely used sorting algorithms due to its efficiency and in-place sorting. It performs best when the pivot is chosen well, balancing the array division. Understanding Quick Sort’s behavior, from how it partitions arrays to how it performs in different scenarios, gives you a powerful tool for tackling sorting problems.
Quick Sort might seem a bit tricky at first, but once you visualize how it works, it becomes an intuitive and valuable algorithm to use in your programming toolkit.
Subscribe to my newsletter
Read articles from Keerthi Ravilla Subramanyam directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Keerthi Ravilla Subramanyam
Keerthi Ravilla Subramanyam
Hi, I'm Keerthi Ravilla Subramanyam, a passionate tech enthusiast with a Master's in Computer Science. I love diving deep into topics like Data Structures, Algorithms, and Machine Learning. With a background in cloud engineering and experience working with AWS and Python, I enjoy solving complex problems and sharing what I learn along the way. On this blog, you’ll find articles focused on breaking down DSA concepts, exploring AI, and practical coding tips for aspiring developers. I’m also on a journey to apply my skills in real-world projects like predictive maintenance and data analysis. Follow along for insightful discussions, tutorials, and code snippets to sharpen your technical skills.