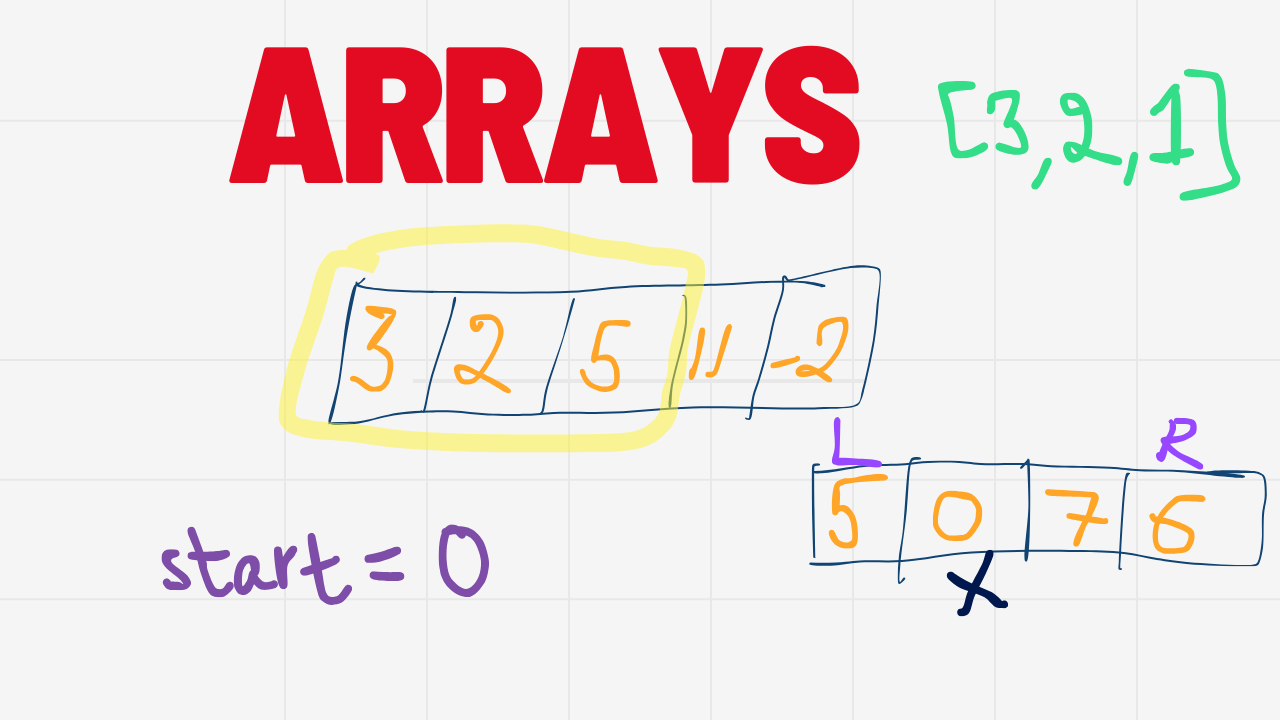
Arrays are fundamental data structures in computer programming, serving as the building blocks for numerous algorithms and applications. Whether you're a beginner programmer or an experienced developer preparing for coding interviews, a solid understanding of arrays and their associated techniques is crucial. In this post, we'll explore the types of arrays and delve into some powerful algorithmic techniques that leverage arrays to solve complex problems efficiently.

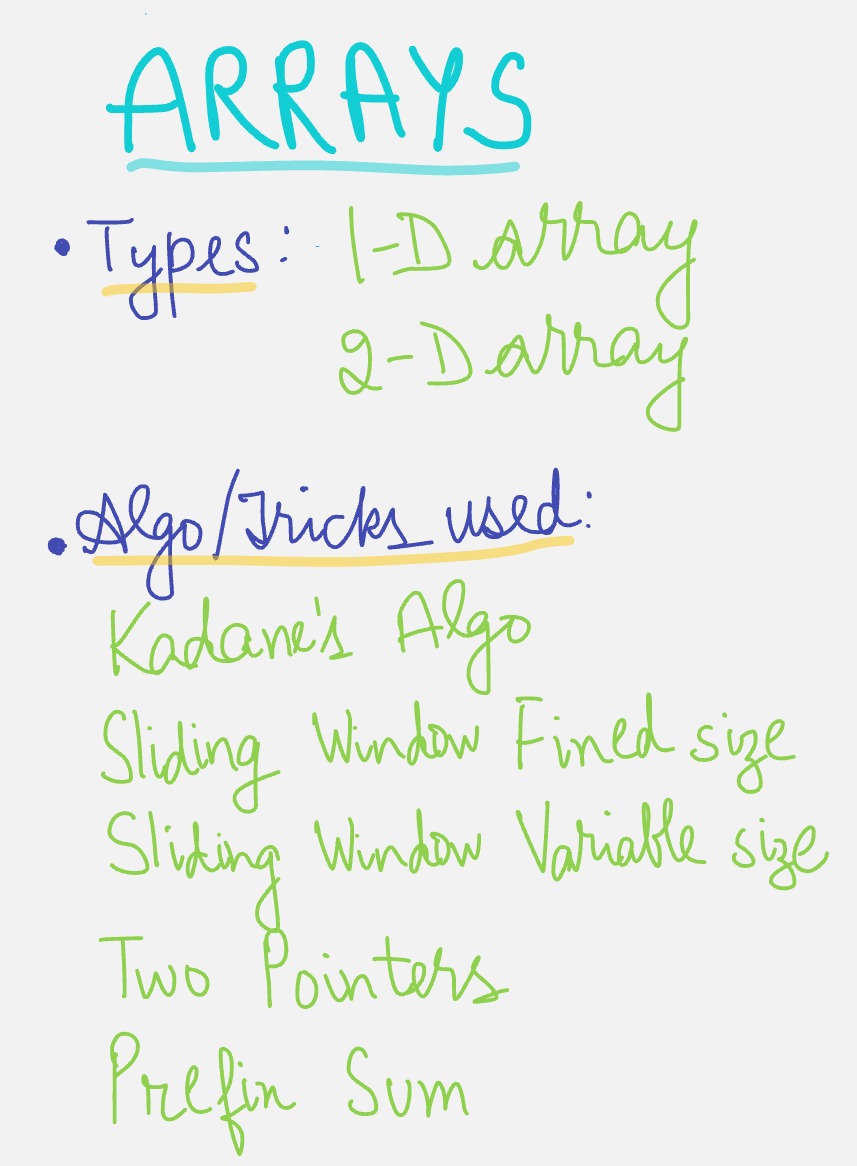
Types of Arrays

Arrays come in different dimensions, but we'll focus on the two most common types: one-dimensional and two-dimensional arrays.

a) One-Dimensional Arrays (1D Arrays)

A one-dimensional array is a linear collection of elements, each identified by an index or a key. It's the simplest form of an array and is often visualized as a row of boxes, each containing a value.

String[] fruits = {"apple", "banana", "cherry", "date"};

Key characteristics:

• Elements are stored in contiguous memory locations.

• Accessing elements is done using their index (usually starting from 0).

• Insertion and deletion at the end take O(1) time, while at an arbitrary position it's O(n).

• Searching in an unsorted array takes O(n) time.

b) Two-Dimensional Arrays (2D Arrays)

A two-dimensional array is essentially an array of arrays, often represented as a matrix or a table with rows and columns.

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

Key characteristics:

• Useful for representing grids, game boards, or mathematical matrices.

• Accessing elements requires two indices: row and column.

• Can be implemented as a single block of memory or as an array of pointers to arrays.

• Time complexity for basic operations is generally O(1), but can be O(n) or O(n^2) for certain operations involving all elements.

  Essential Array Techniques and Algorithms

  Now that we've covered the types of arrays, let's explore some powerful techniques and algorithms that are frequently used with arrays.

a) Kadane's Algorithm

Kadane's algorithm is used to find the contiguous subarray within a one-dimensional array of numbers that has the largest sum.

How it works:

1. Initialization:

   • maxSum starts with the first array element to handle all-negative arrays.

   • curSum starts at 0, representing the current subarray sum.

2. Iterative Process: For each element in the array:

   • Reset curSum to 0 if it's negative (abandoning unproductive subarrays).

   • Add the current element to curSum.

   • Update maxSum if curSum is larger, tracking the best subarray sum.

3. Result: After processing all elements, maxSum contains the maximum subarray sum, which is then returned.

    public static int kadanes(int[] nums) {
            int maxSum = nums[0];
            int curSum = 0;
   
            for (int n : nums) {
                curSum = Math.max(curSum, 0);
                curSum += n;
                maxSum = Math.max(maxSum, curSum);
            }
            return maxSum;
        }
   

4. Time complexity: O(n)

b) Sliding Window Technique

The sliding window technique is used to process arrays or strings by maintaining a "window" of elements and sliding it through the data structure.

i) Fixed-Size Sliding Window

In a fixed-size sliding window, the size of the window remains constant throughout the traversal.

• Useful for problems involving subarrays or substrings of a fixed length.

• Time complexity is often O(n), where n is the size of the array or string.

How it works:

1. Sliding Window Setup:

   • Use a HashSet (window) to track unique elements within a window of size k.

   • Slide this window through the array using two pointers, L (left) and R (right).

2. Window Management and Duplicate Check:

   • For each new element (at R):

     • If the window size exceeds k, remove the leftmost element and move L.

     • Check if the current element is already in the window. If so, return true.

     • Otherwise, add the current element to the window.

3. Result:

   • If no duplicates are found after processing all elements, return false.

// Check if array contains a pair of duplicate values,
public class SlidingWindowFixedSize {
    public static boolean closeDuplicates(int[] nums, int k) {
        HashSet<Integer> window = new HashSet<>(); // Cur window of size <= k
        int L = 0;

        for (int R = 0; R < nums.length; R++) {
            if (R - L + 1 > k) {
                window.remove(nums[L]);
                L++;
            }
            if (window.contains(nums[R])) {
                return true;
            }
            window.add(nums[R]);
        }
        return false;
    }
}

ii) Variable-Size Sliding Window

In a variable-size sliding window, the size of the window can change during the traversal.

• Useful for problems where the size of the subarray or substring is not fixed.

• Often involves expanding and contracting the window based on certain conditions.

How it works:

1. Sliding Window Expansion:

   • Initialize a sliding window with left pointer L and right pointer R.

   • Expand the window by moving R to the right, adding each new element to the total sum.

2. Window Contraction and Length Update:

   • When total becomes greater than or equal to the target:

     • Update length to the minimum of current length and window size (R - L + 1).

     • Contract the window from the left by subtracting nums[L] from total and incrementing L.

     • Continue this contraction while total remains greater than or equal to target.

3. Result Handling:

   • After processing all elements, if length remains Integer.MAX_VALUE, return 0 (no valid subarray found).

   • Otherwise, return the length of the shortest subarray meeting the condition.

// Find length of minimum size subarray where the sum is 
// greater than or equal to the target: O(n)
public static int shortestSubarray(int[] nums, int target) {
    int L = 0, total = 0;
    int length = Integer.MAX_VALUE;

    for (int R = 0; R < nums.length; R++) {
        total += nums[R];
        while (total >= target) {
            length = Math.min(R - L + 1, length);
            total -= nums[L];
            L++;
        }
    }

    if (length ==  Integer.MAX_VALUE) {
        return 0;
    } 
    return length;
   }
}

d) 2 Pointers

The two pointers technique involves using two pointers to traverse an array or string, often moving in opposite directions or at different speeds.

• Often used to solve problems with O(n) time complexity and O(1) space complexity.

• Useful for problems involving searching, reversing, or finding pairs in sorted arrays.

How it works:

1. Initial Setup:

   • Two pointers are initialized: L at the start of the array (index 0) and R at the end (last index).

   • The input array nums is assumed to be sorted in ascending order.

2. Two-Pointer Iteration:

   • The function enters a while loop that continues as long as L is less than R.

   • In each iteration, it calculates the sum of the elements at positions L and R.

3. Sum Comparison and Pointer Adjustment:

   • If the sum is greater than the target, R is decremented to reduce the sum.

   • If the sum is less than the target, L is incremented to increase the sum.

   • If the sum exactly matches the target, the function immediately returns the current indices [L, R].

4. Result Handling:

   • If the loop completes without finding a match (which shouldn't happen if there's guaranteed to be one solution), the function returns null.

   • This approach efficiently finds the solution in O(n) time complexity by leveraging the sorted nature of the input array.

   •     //  Given a sorted array of integers, return the indices
         //  of two elements (in different positions) that sum up to
         //  the target value. Assume there is exactly one solution.
         //  O(n)
         public class TwoPointer {
         public static int[] targetSum(int[] nums, int target) {
             int L = 0, R = nums.length - 1;
             while (L < R) {
                 if (nums[L] + nums[R] > target) {
                     R--;
                 } else if (nums[L] + nums[R] < target) {
                     L++;
                 } else {
                     return new int[] {L, R};
                 }    
             }
             return null;
         }
     

c) Prefix Sum

Prefix sum is a technique where you precompute cumulative sums of array elements to efficiently answer range sum queries.

How it works:

1. Constructor and Prefix Sum Calculation:

   • The constructor takes an array of integers (nums) as input.

   • It initializes an ArrayList prefix to store cumulative sums.

   • It iterates through nums, calculating a running total and adding each cumulative sum to prefix.

2. Prefix Sum Array Structure:

   • After construction, prefix contains cumulative sums where prefix.get(i) represents the sum of all elements from index 0 to i in the original array.

   • This precomputation allows for efficient range sum queries.

3. Range Sum Calculation Method:

   • The rangeSum method calculates the sum of elements between indices left and right (inclusive).

   • It uses the formula: sum(left to right) = prefix[right] - prefix[left-1]

   • A special case is handled when left is 0, avoiding index out of bounds.

4. Efficiency:

   • Construction time is O(n), where n is the length of the input array.

   • Each rangeSum query takes O(1) time, as it involves only simple arithmetic operations.

public class PrefixSum {

    List<Integer> prefix;

    public PrefixSum(int[] nums) {
        prefix = new ArrayList<>();
        int total = 0;
        for (int n : nums) {
            total += n;
            prefix.add(total);
        }
    }

    public int rangeSum(int left, int right) {
        int preRight = prefix.get(right);
        int preLeft = left > 0 ? prefix.get(left - 1) : 0;
        return (preRight - preLeft);      
    }
}