Hierarchical Navigable Small World (HNSW)

Sai Prasanna MaharanaSai Prasanna Maharana
6 min read

Table of contents

Certainly!

Hierarchical Navigable Small World (HNSW) is a popular algorithm used in vector databases for efficient approximate nearest neighbor (ANN) search in high-dimensional spaces. It is particularly effective for large-scale datasets due to its scalability and performance. When combined with cosine similarity as the distance metric, HNSW enables fast and accurate retrieval of vectors based on their angular similarity.

Table of Contents

  1. Introduction to HNSW

  2. Understanding Cosine Similarity

  3. How HNSW Works with Cosine Similarity

    • Building the HNSW Graph

    • Navigating the Graph for Search

  4. Implementation Steps

    • Index Construction

    • Query Processing

  5. Code Example Using FAISS

  6. Advantages of HNSW with Cosine Similarity

  7. Considerations and Best Practices

  8. Conclusion

  9. References

1. Introduction to HNSW

HNSW (Hierarchical Navigable Small World) is an algorithm for approximate nearest neighbor search based on the concept of navigable small-world graphs. It constructs a multi-layer graph where each layer represents a network of connections between data points (vectors). The algorithm efficiently navigates through these layers to find the nearest neighbors of a query vector.

Key Features:

  • Hierarchical Structure: Multiple layers with decreasing levels of abstraction.

  • Navigability: Efficient traversal using greedy search strategies.

  • Scalability: Handles millions of vectors with high performance.

2. Understanding Cosine Similarity

Cosine similarity measures the cosine of the angle between two vectors in a multi-dimensional space. It is defined as:

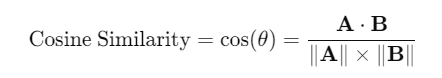
  • Range: The value ranges from -1 to 1.

  • Interpretation:

    • 1: Vectors are identical in direction.

    • 0: Vectors are orthogonal (no similarity).

    • -1: Vectors are diametrically opposed.

Why Use Cosine Similarity?

  • Scale Invariance: Focuses on the orientation rather than magnitude.

  • Common in NLP: Frequently used in text embeddings where direction matters more than magnitude.

3. How HNSW Works with Cosine Similarity

a. Building the HNSW Graph

  1. Initialization:

    • Start with an empty graph.

    • Determine the maximum layer Lmax based on the logarithm of the number of elements.

  2. Insertion of Nodes:

    • Random Level Assignment: Each new vector is assigned a random maximum layer L (up to Lmax) following an exponential distribution.

    • Connecting Nodes:

      • For each layer from Lmax down to level 0:

        • Greedy Search: Find the closest nodes in the current layer to the new vector using cosine similarity.

        • Establish Connections: Connect the new vector to these nodes, forming edges in the graph.

      • Neighbor Selection: Limit the number of connections (controlled by parameter M) to balance graph density and search speed.

  1. Starting Point:

    • Begin the search from an entry point at the top layer (Lmax).

  2. Greedy Search:

    • At each layer:

      • Current Node: Start from the current node.

      • Neighbors Exploration: Examine the neighbors of the current node.

      • Distance Calculation: Compute cosine similarity between the query vector and neighboring nodes.

      • Move Decision: Move to the neighbor with the highest cosine similarity (closest in angular distance).

  3. Layer Transition:

    • If no closer neighbor is found at the current layer, descend to the next lower layer.

    • Repeat the greedy search at each layer until reaching layer 0.

  4. Final Search at Layer 0:

    • Perform a more thorough search (e.g., beam search) to refine the nearest neighbors.

4. Implementation Steps

a. Index Construction

  • Data Preparation: Normalize all vectors to unit length to use cosine similarity effectively.

      import numpy as np

  def normalize_vectors(vectors):
      norms = np.linalg.norm(vectors, axis=1, keepdims=True)
      return vectors / norms

  • Graph Building: Use an HNSW library (e.g., FAISS, Annoy, hnswlib) to build the index.

b. Query Processing

  • Query Normalization: Normalize the query vector to unit length.

  • Similarity Search: Use the HNSW index to find the nearest neighbors based on cosine similarity.

5. Code Example Using FAISS

Let's demonstrate how HNSW works with cosine similarity using the FAISS library.

a. Install FAISS

pip install faiss-cpu  # For CPU
# or
pip install faiss-gpu  # For GPU

b. Sample Dataset

import numpy as np

# Generate a sample dataset of 10,000 128-dimensional vectors
np.random.seed(42)
data = np.random.random((10000, 128)).astype('float32')

c. Normalize Vectors

def normalize_vectors(vectors):
    norms = np.linalg.norm(vectors, axis=1, keepdims=True)
    return vectors / norms

data_normalized = normalize_vectors(data)

d. Build the HNSW Index

import faiss

d = data.shape[1]  # Dimension of vectors

# Use Inner Product (Dot Product) for Cosine Similarity
index = faiss.index_factory(d, "HNSW32", faiss.METRIC_INNER_PRODUCT)

# Set HNSW parameters (optional)
hnsw_param = index.hnsw
hnsw_param.nb_neighbors = 32  # M parameter
hnsw_param.efConstruction = 200  # Controls index time and accuracy

# Train the index if necessary (not required for HNSW with flat vectors)

# Add vectors to the index
index.add(data_normalized)

# Normalize the query vector
query_vector = np.random.random((1, 128)).astype('float32')
query_vector_normalized = normalize_vectors(query_vector)

# Set search parameters
index.hnsw.efSearch = 50  # Controls search speed vs. accuracy

# Perform the search
k = 5  # Number of nearest neighbors
distances, indices = index.search(query_vector_normalized, k)

# Display results
print("Nearest neighbors (indices):", indices)
print("Distances (cosine similarity):", distances)

Note: In FAISS, when using METRIC_INNER_PRODUCT, the distances returned are the inner product values. Since the vectors are normalized, the inner product is equivalent to cosine similarity.

f. Explanation

  • Normalization: By normalizing vectors to unit length, the inner product becomes cosine similarity.

  • Index Creation: The HNSW32 specifies that each node in the graph will have up to 32 connections.

  • Search Parameters: efSearch controls the trade-off between search speed and recall.

6. Advantages of HNSW with Cosine Similarity

  • Efficient Retrieval: HNSW provides sub-linear query time complexity, making it suitable for large datasets.

  • High Recall: Capable of achieving high recall rates with appropriate tuning.

  • Scalability: Can handle millions of vectors with reasonable memory consumption.

  • Flexibility: Supports various distance metrics, including cosine similarity.

7. Considerations and Best Practices

  • Vector Normalization:

    • Essential when using cosine similarity to ensure accurate distance computations.

    • Normalization should be applied consistently to both index vectors and query vectors.

  • Parameter Tuning:

    • M (nb_neighbors): Controls the graph's connectivity. Higher values improve accuracy but increase memory usage.

    • efConstruction: Affects the quality of the index during construction. Higher values yield better recall.

    • efSearch: Adjusts the search depth. Increasing efSearch improves recall at the expense of query time.

  • Memory Consumption:

    • HNSW indexes can consume significant memory, especially with large M values.

    • Monitor memory usage and adjust parameters accordingly.

  • Distance Metric Consistency:

    • Ensure that the distance metric used during index construction matches the metric used during search.

    • In FAISS, use METRIC_INNER_PRODUCT with normalized vectors for cosine similarity.

  • Library Selection:

    • Choose a library that supports HNSW and cosine similarity, such as FAISS or hnswlib.

8. Conclusion

HNSW is a powerful algorithm for approximate nearest neighbor search in vector databases. When combined with cosine similarity, it enables efficient and accurate retrieval of vectors based on their angular relationships. By constructing a hierarchical graph and navigating it using greedy search strategies, HNSW provides a scalable solution suitable for production environments handling large-scale, high-dimensional data.

9. References

0
Subscribe to my newsletter

Read articles from Sai Prasanna Maharana directly inside your inbox. Subscribe to the newsletter, and don't miss out.

algorithmsgenaiembedded

Written by

Sai Prasanna Maharana
Sai Prasanna Maharana