Introduction to Graphs | Data Structures and Algorithms Day #20

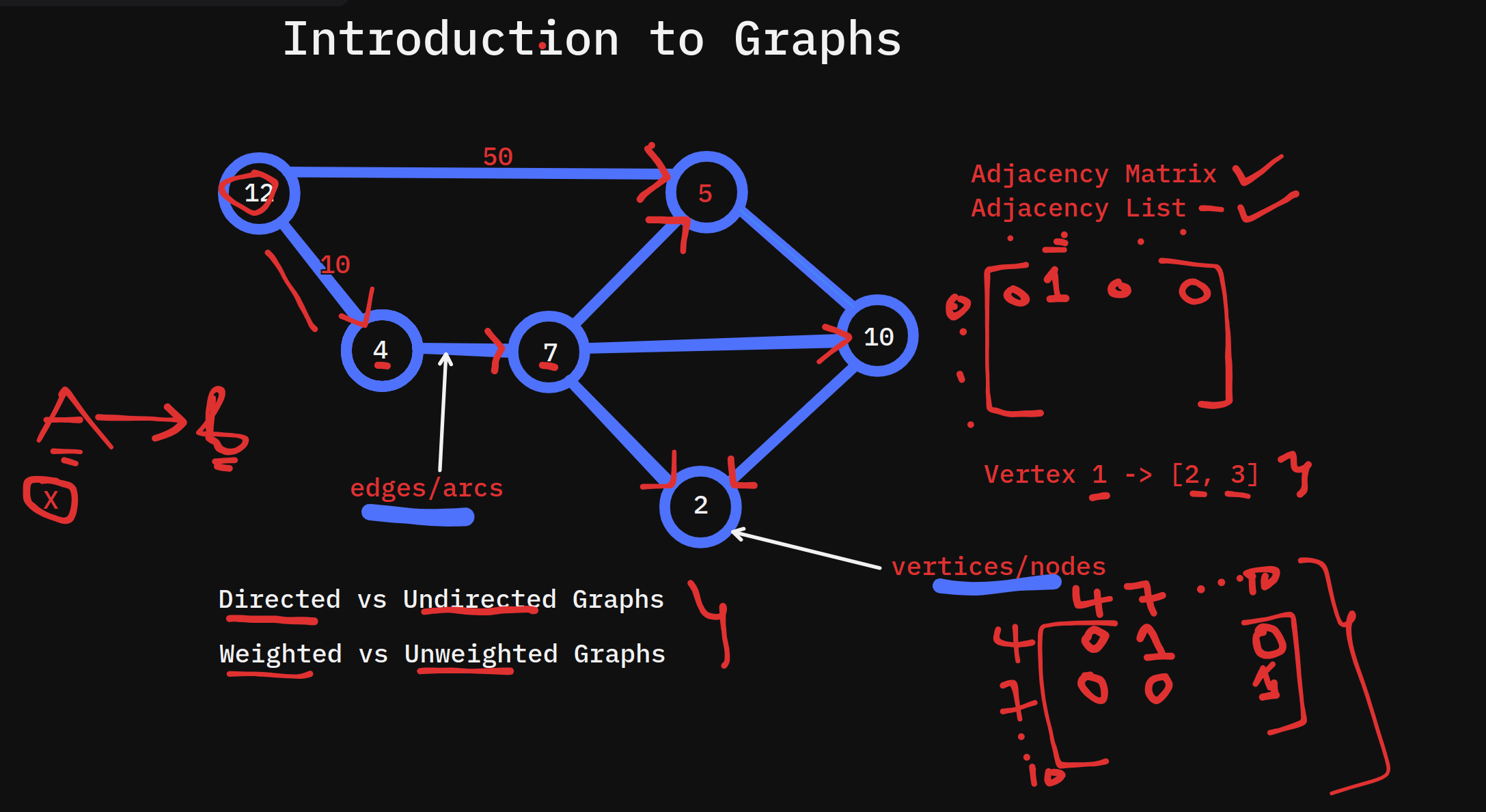
Graphs are one of the most powerful and versatile data structures in computer science. Whether it’s modeling social networks, finding the shortest path in maps, or building recommendation engines, graphs play a crucial role in solving complex problems. This guide provides an introduction to graphs, covering their key concepts, types, real-world applications, and implementations in Python and JavaScript.

If you’re already familiar with hash tables and how they provide efficient lookups, you’ll appreciate how graphs complement these concepts in more dynamic scenarios. Check out What is a hash table? and How hash tables work for a quick recap before diving into graphs.

---

What is a Graph?

A graph is a data structure used to represent a collection of nodes (vertices) and the connections (edges) between them. It’s a way to model relationships between elements—making graphs essential for network analysis, search algorithms, and optimization tasks.

For example:

• Social networks represent users as nodes and friendships as edges.

• Navigation systems use nodes for locations and edges for roads.

• Recommendation engines link users with products through common interests.

---

Basic Concepts and Terminology

Here are key terms to understand graphs:

• Vertex (Node): A point representing an entity or object (e.g., a person or city).

• Edge: A connection between two nodes.

• Directed Graph: Edges have direction (A → B), indicating a one-way relationship.

• Undirected Graph: Edges don’t have direction (A - B), meaning the relationship is bidirectional.

• Weighted Graph: Each edge carries a weight (e.g., distance or cost).

• Cyclic Graph: Contains cycles—paths that start and end at the same node.

• Acyclic Graph: Does not contain cycles.

Here’s a simple diagram illustrating a graph with nodes and edges:
Diagram:
(A)---(B)
|
(C)---(D)

---

Types of Graphs

1. Directed vs. Undirected Graphs:

   • Directed Graph: A → B (One-way relationship)

   • Undirected Graph: A - B (Two-way relationship)

2. Weighted vs. Unweighted Graphs:

   • Weighted Graph: Each edge has a numeric value (e.g., distances).

   • Unweighted Graph: All edges are equal with no specific value.

3. Cyclic vs. Acyclic Graphs:

   • Cyclic Graph: Has loops or cycles.

   • Acyclic Graph: No cycles; a DAG (Directed Acyclic Graph) is often used in scheduling or dependency management.

---

Graph Representations in Code

Graphs can be represented using adjacency matrices or adjacency lists.

Adjacency List Representation

An adjacency list stores a graph as a dictionary, where each key is a node, and the value is a list of connected nodes.

Python Example

graph = {
    'A': ['B', 'C'],
    'B': ['D'],
    'C': ['D'],
    'D': []
}
print(graph)  # {'A': ['B', 'C'], 'B': ['D'], 'C': ['D'], 'D': []}

JavaScript Example

const graph = {
    'A': ['B', 'C'],
    'B': ['D'],
    'C': ['D'],
    'D': []
};
console.log(graph);  // { A: [ 'B', 'C' ], B: [ 'D' ], C: [ 'D' ], D: [] }

Adjacency Matrix Representation

An adjacency matrix is a 2D array where each element indicates if an edge exists between two nodes. This method is less space-efficient than adjacency lists but faster for dense graphs.

---

Real-World Applications of Graphs

Graphs are used in a wide range of practical applications:

• Social Networks: Representing users and their connections.

• Web Crawling and Search Engines: Graphs model how websites are linked.

• Route Planning: Algorithms like Dijkstra's or A search* use graphs to find the shortest path.

• Task Scheduling: Directed Acyclic Graphs (DAGs) are used in task scheduling and dependency management.

---

Common Graph Algorithms

Understanding graphs requires familiarity with key algorithms used to traverse and manipulate them:

1. Breadth-First Search (BFS): Explores nodes layer by layer.

2. Depth-First Search (DFS): Explores as far as possible along each branch before backtracking.

3. Dijkstra’s Algorithm: Finds the shortest path in weighted graphs.

4. Topological Sort: Orders nodes in a DAG based on dependencies.

---

Time Complexity Analysis

Using graphs effectively requires knowing the time complexity of common operations:

• Adjacency List Lookup: O(V + E) (V = number of vertices, E = number of edges).

• Adjacency Matrix Lookup: O(V²).

These time complexities make adjacency lists more efficient for sparse graphs, while adjacency matrices are ideal for dense graphs.

For a deeper dive into time complexity, check out How hash tables work.

---

Conclusion

Graphs are a fundamental part of computer science, helping solve real-world problems like route planning, network analysis, and task scheduling. Whether represented as adjacency lists or matrices, graphs provide a flexible way to model relationships between elements.

---

Call to Action

Now that you understand the basics of graphs, try implementing your own graph algorithms like BFS or Dijkstra’s. Experiment with real-world datasets—like a social network or a map—and explore graph traversal algorithms for more insights.

Got questions? Drop them in the comments or share your experience working with graphs!