Chapter 3 : Time and Space Complexity

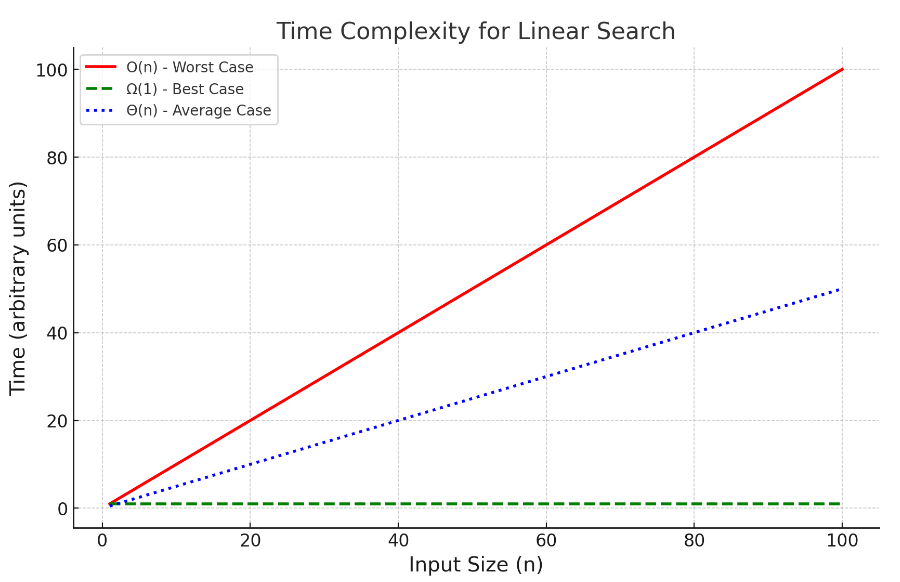
Dijkstra’s Algorithm, Sieve of Eratosthenes, Bellman-Ford Algorithm, Kruskal’s Algorithm, Floyd-Warshall Algorithm, and many more—do you know why these fancy names exist? Or, rather, why does DSA exist at all? Of course, we need different data structures to store different data types, but how do they come about, and why algorithms? The answer is one word: complexity.

Let me uncomplexity this complexity for yoụ

Before that here is a question for you :

The same algorithm runs on a 10-year-old i3 machine (let's say M1) and a MacBook M3 (let's say M2). It takes 10 seconds on M1 and 1 second on M2. Which machine has better time complexity?

M3, right? No, time complexity is independent of the machine.

Time complexity refers to how time will increase as input increases.

For eg -

for(int i = 0; i < n; i++) {
    System.out.println(n);
}

In this example, let's say printing each element takes 1 second. So, for an input of 100, it will take 100 seconds, and it will increase further as n increases. Therefore, we can say its time complexity is O(n).

What is O(n)?

O(n), or linear time complexity, means that the time taken by the algorithm increases proportionally with the size of the input. If n doubles, the time taken also roughly doubles.

In this case, the loop runs exactly n times, so the time grows linearly with n. Hence, the time complexity is O(n).

Before moving forward, let's understand the terminology first.

1. Big O (O): Upper Bound

Big O notation represents the worst-case time complexity of an algorithm. It gives an upper limit on the time or space an algorithm could take, regardless of specific input.

Big O describes the maximum growth rate of a function as the input size (n) increases.

Example:

public int linearSearch(int[] arr, int target) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == target) {
            return i; // Target found
        }
    }
    return -1; // Target not found
}

In the worst-case, the algorithm will have to search through the entire array to either find the target at the last position or to conclude that the target is not in the array at all.

If the target is at the last position or doesn't exist, the loop runs n times, where n is the length of the array.

So, the worst-case time complexity is: O(n).

2. Big Omega (Ω): Lower Bound

Big Omega notation provides a best-case scenario, or the minimum amount of time an algorithm will take.

It describes the lower bound on the time complexity: no matter what the input, the algorithm will take at least this amount of time.

Example:

public int linearSearch(int[] arr, int target) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == target) {
            return i; // Target found
        }
    }
    return -1; // Target not found
}

In the best-case, the target is found at the first position in the array. The algorithm will only run the loop once before returning the index.

If the target is at the first position, the algorithm completes in just one iteration.

So, the best-case time complexity is: Ω(1).

3. Theta (Θ): Tight Bound

Theta notation is used when an algorithm's upper bound and lower bound are the same. It provides a tight bound, meaning the algorithm will take this amount of time in both the best and worst cases.

It describes the exact rate of growth for an algorithm, where both the best-case and worst-case times grow at the same rate.

Example:

public int linearSearch(int[] arr, int target) {
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] == target) {
            return i; // Target found
        }
    }
    return -1; // Target not found
}

In the average-case, the target is equally likely to be anywhere in the array. On average, the algorithm will check around half of the elements before finding the target.

On average, the algorithm runs n/2 times, which simplifies to n as constants are ignored in time complexity analysis.

So, the average-case time complexity is: Θ(n).

Summary of Time Complexity:

O(n): Upper bound (worst-case).

Ω(n): Lower bound (best-case).

Θ(n): Exact bound (tight bound, both best and worst case grow at the same rate).

Now, before diving into examples, let's understand some rules.

1. Ignore Constants

Constant factors, whether multiplying or adding, don't affect the overall growth rate of the algorithm as n grows larger.

Examples:

O(2n) → O(n) (ignore the constant multiplier 2).

O(500) → O(1) (constant time remains constant, no matter the size of n).

2. Take the Highest-Order Term

When there are multiple terms in the complexity expression, the term with the highest degree dominates as the input size (n) increases. Lower-order terms become insignificant.

Examples:

O(n^2 + n) → O(n^2).

O(n^3 + n^2 + n) → O(n^3).

3. Drop Lower-Order Terms

When multiple terms grow at different rates, we keep only the fastest-growing one, as it will eventually outgrow the others for sufficiently large n.

Examples:

O(n^2 + n + 1) → O(n^2).

O(n^3 + n^2 + n + log n) → O(n^3).

4. Additive vs. Multiplicative Terms

• If two independent loops or processes run one after the other (sequentially), their complexities are added.

• If loops are nested, their complexities are multiplied.

  Examples:

  • Additive: Two separate loops:

      for (int i = 0; i < n; i++) { /* O(n) */ }
      for (int j = 0; j < n; j++) { /* O(n) */ }
    

    Time complexity = O(n) + O(n) = O(n).

  • Multiplicative: Nested loops:

      for (int i = 0; i < n; i++) {
          for (int j = 0; j < n; j++) {
              /* O(1) */
          }
      }
    

    Time complexity = O(n) * O(n) = O(n^2).

5. Logarithmic Time

• Logarithmic time occurs when the input size is repeatedly divided, such as in binary search.

• The time complexity is O(log n), which grows much slower than linear time O(n).

  Examples: Binary Search: Each step reduces the problem size by half:

    while (low <= high) {
        mid = (low + high) / 2;
        if (arr[mid] == target) break;
        else if (arr[mid] < target) low = mid + 1;
        else high = mid - 1;
    }
  

  Time complexity = O(log n).

6. Polynomial Time

If an algorithm has terms like n^2, n^3, etc., it is said to have polynomial time complexity.

Examples:

O(n^2): Common in algorithms with nested loops where both loops iterate over the entire input.

7. Exponential Time

Exponential time, such as O(2^n), grows extremely fast and becomes impractical for large inputs. This often occurs in brute-force algorithms.

Examples: Recursive algorithms that branch extensively:

int fibonacci(int n) {
    if (n <= 1) return n;
    return fibonacci(n - 1) + fibonacci(n - 2);
}

Time complexity = O(2^n).

8. Factorial Time

Factorial time O(n!) is extremely inefficient and typically arises in algorithms that generate all possible permutations.

Examples: Generating all permutations of an array.

Now, let's understand space complexity.

Just like time complexity measures the time an algorithm takes to run as the input size increases, space complexity measures the amount of memory or space an algorithm uses as the input size grows.

Why is space complexity important?

In certain cases, memory can be a limiting factor. Even if an algorithm runs fast, it could still be impractical if it requires too much memory, especially with large datasets. Understanding space complexity helps ensure your program doesn't use more memory than available.

Components of Space Complexity

Space complexity includes:

1. Fixed Part: The space required by variables, constants, and other static elements (which doesn't depend on the input size). This is usually considered as constant space (O(1)).

2. Variable Part: The space required for dynamically allocated memory, such as arrays, objects, and recursion stack space, which grows with the input size (n).

The total space complexity is a combination of both the fixed part and variable part.

Components of Space Complexity

Space complexity includes:

1. Fixed Part: The space required by variables, constants, and other static elements (which doesn't depend on the input size). This is usually considered as constant space (O(1)).

2. Variable Part: The space required for dynamically allocated memory, such as arrays, objects, and recursion stack space, which grows with the input size (n).

The total space complexity is a combination of both the fixed part and variable part.

Examples

1. Constant Space (O(1))

public int addTwoNumbers(int a, int b) {
    return a + b;
}

Here, we only have two variables a and b, and the space needed for these variables doesn't change with the input size. So, the space complexity is constant:

Space Complexity: O(1)

2. Linear Space (O(n))

public int[] createArray(int n) {
    int[] arr = new int[n];  // Dynamically allocates space for n elements
    return arr;
}

In this case, the array arr requires space that increases linearly with the input size n. As n grows, the memory usage grows proportionally.

Space Complexity: O(n)

3. Recursive Algorithm

public int factorial(int n) {
    if (n == 0) return 1;
    return n * factorial(n - 1);
}

Here, each time factorial is called, a new stack frame is made. For an input size n, the function is called n times, and each call adds to the stack. So, the space complexity is proportional to n.

Space Complexity: O(n)

4. Logarithmic Space (O(log n))

public void binarySearch(int[] arr, int target, int low, int high) {
    if (low > high) return;

    int mid = (low + high) / 2;

    if (arr[mid] == target) return;
    else if (arr[mid] < target) binarySearch(arr, target, mid + 1, high);
    else binarySearch(arr, target, low, mid - 1);
}

In this recursive version of binary search, the memory usage grows with the depth of the recursive calls. Since the array is halved at each step, the recursion depth is proportional to log n. Hence, the space complexity is:

Space Complexity: O(log n)

Summary of Space Complexity

O(1): Constant space. The algorithm uses a fixed amount of memory.

O(n): Linear space. The algorithm’s memory usage grows linearly with input size.

O(log n): Logarithmic space. Typically seen in divide-and-conquer algorithms.

O(n^2): Quadratic space. Typically used when storing all pairs of data.

Now lets dive into some examples :

GitHub URL - https://github.com/vaishdwivedi1/DSA

Here are some practice questions if you have any doubt just ask me!