Sorting Simplified: Bubble, Selection, Insertion, and Cycle Sort Explained

Sorting is one of the most critical operations in DSA, forming the foundation of many complex algorithms. I explored various sorting algorithms like Bubble Sort, Selection Sort, Insertion Sort, and Cycle Sort. Each of these algorithms offers different strengths and weaknesses, and solving LeetCode problems helped me truly understand their real-world applications.

Here’s what I learned.

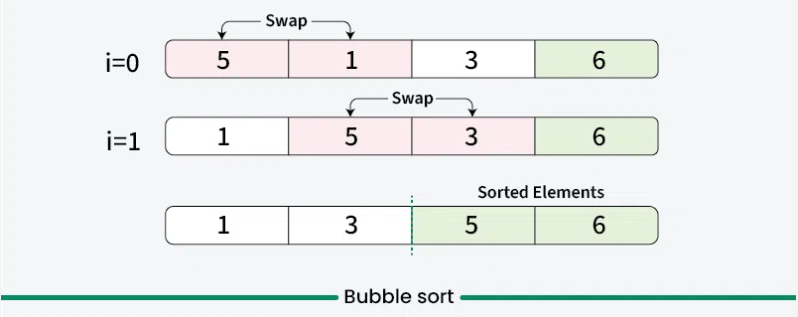
Bubble Sort

Bubble Sort is one of the simplest sorting algorithms. It works by repeatedly swapping adjacent elements if they are in the wrong order. Although easy to implement, Bubble Sort is not efficient for larger datasets, with a time complexity of O(n²).

static int[] bubbleSort(int[] arr) {

    for (int i = 0; i < arr.length; i++) {
        boolean swapped = false;
        for (int j = 1; j < arr.length - i; j++) {
            if (arr[j - 1] > arr[j]) {
                int temp = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = temp;
                swapped=true;
            }
        }
        if (!swapped){
            break;
        }
    }
    return arr;
}

Key Learning Points

Bubble Sort performs well for small datasets or nearly sorted arrays. However, as I practiced on larger problems, I realized the inefficiency compared to more optimized algorithms. Nevertheless, it’s a great starting point to understand the concept of swapping and passes.

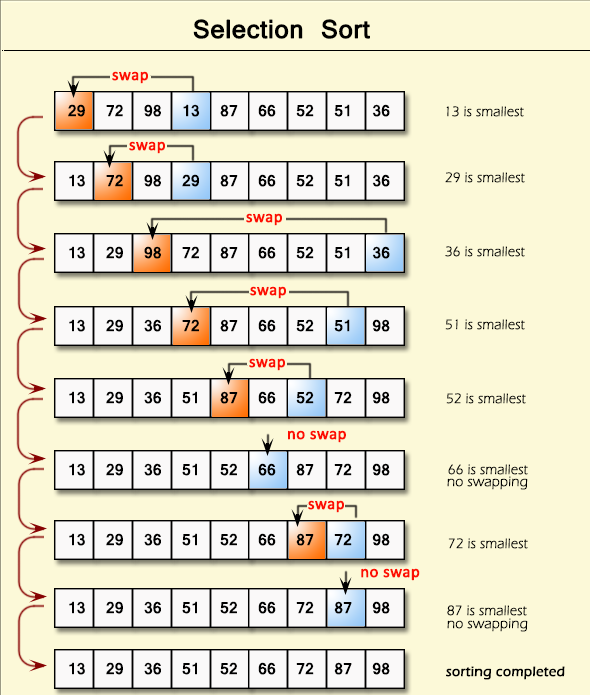
Selection Sort

Selection Sort works by repeatedly selecting the smallest (or largest) element from the unsorted portion of the array and placing it in its correct position. Like Bubble Sort, its time complexity is O(n²), but it generally performs better in practice since it makes fewer swaps.

static void selection(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        // find the max item in the remaining array and swap with correct index
        int last = arr.length - i - 1;
        int maxIndex = getMaxIndex(arr, 0, last);
        swap(arr, maxIndex, last);
    }
}
static int getMaxIndex(int[] arr, int start, int end) {
    int max = start;
    for (int i = start; i <= end; i++) {
        if (arr[max] < arr[i]) {
            max = i;
        }
    }
    return max;
}

Why Selection Sort is Important

I found selection sort interesting because it teaches the importance of minimizing swaps. Although it’s not the most efficient sorting algorithm, it’s a good next step after learning Bubble Sort and helps build intuition for sorting techniques.

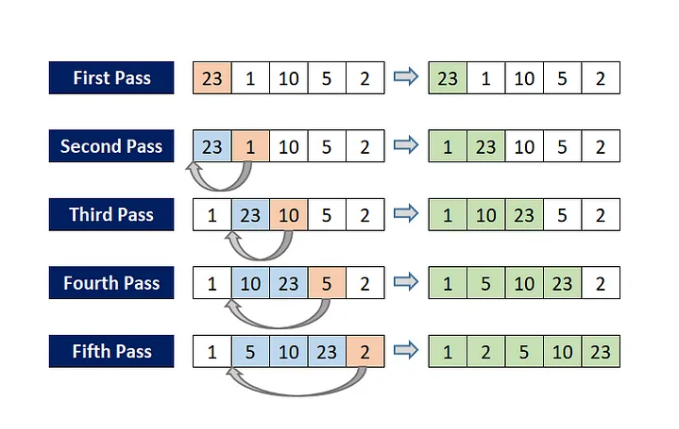
Insertion Sort

Insertion Sort builds the sorted array one element at a time by repeatedly inserting new elements into their correct position and minimizing the operational space on the array one by one. Its time complexity is O(n²) for the worst case, but it performs well on small or nearly sorted datasets.

static void insertion(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = i+1; j > 0; j--) {
            if (arr[j] < arr[j-1]) {
                swap(arr, j, j-1);
            } else {
                break;
            }
        }
    }
}
static void swap(int[] arr, int i, int j) {
        int temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
    }

What I Enjoyed About Insertion Sort

What stood out to me about insertion sort was its simplicity and its ability to sort efficiently when the array is already almost sorted.

Cycle Sort

Cycle Sort is a unique algorithm used primarily when memory writes are a significant concern. It minimizes the number of writes by moving each element directly to its final position. With a time complexity of O(n²), it’s not the most efficient, but it is optimal in terms of memory usage.

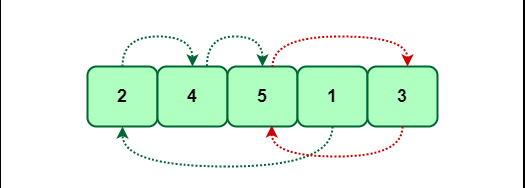
Working of Cycle Sort

In Cycle sort, We select an element and put it at its correct index. It works when elements in the array are in the range (1,n) or (0,n). For Example, if we have an array [1,3,5,2,4], we must apply cycle sort. We’ll use the formulae as, for each element the index = element -1 as the array is (1,n).

static int[] cyclicSort1(int[] arr){
        int i=0;
        while(i<arr.length){
            int correct = arr[i] -1; // for array in range (1,n)
            if (arr[i] != arr[correct]){
                swap(arr, i , correct);
            }
            else{
                i++;
            }
        }
        return arr;
    }
private static void swap(int[] arr, int i, int j) {
        int temp = arr[j];
        arr[j] = arr[i];
        arr[i] = temp;
    }

My Experience with Cycle Sort

Cycle Sort was the most challenging algorithm I learned in this section. I hadn't encountered the idea of minimizing writes while maintaining sorting order before. Although it’s not a widely used algorithm in practice, it’s a fantastic learning experience.

LeetCode Problems Solved

To solidify my understanding, I solved LeetCode problems related to these sorting algorithms. Each problem presented unique challenges and helped me grasp how these algorithms work under different conditions. Here are some of the problems I tackled:

• First Missing Positive (Hard)

• Set Mismatch (Easy)

• Find All Duplicates in an Array (Medium)

• Find the Duplicate Number (Medium)

• Find All Numbers Disappeared in an Array (Easy)

• Missing Number (Easy)

Code Repository

All my sorting algorithm implementations are available in my GitHub repository. You can explore the code, understand how each algorithm works, and try it out on different datasets.

Here’s the link to my repository: GitHub Repo

Conclusion

Learning sorting algorithms like Bubble Sort, Selection Sort, Insertion Sort, and Cycle Sort has been a rewarding experience. Each algorithm has its place in computer science, and solving LeetCode problems has helped me understand their strengths and limitations in real-world applications. In the coming weeks, I’ll dive deeper into more advanced sorting techniques and continue building DSA knowledge.