Solved pattern problem in a easy way

We all encounter challenges in building logic when trying to solve pattern problems. Questions like how to create the logic, what range to use for the loop, and how to apply if-else statements are common among students. I have faced these problems several times as well. So to solve this we can use a very easy template to do this pattern problem.

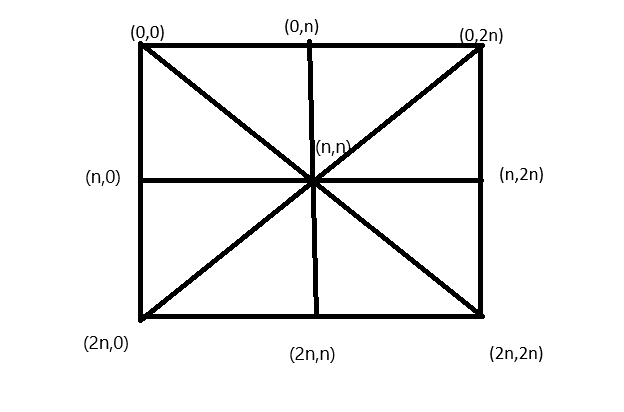
Let's consider this image. We will use this template to understand the process of calculating the logic. Here, we can see a square shape divided into 8 segments, and we assign coordinates to them accordingly. Before solving the difficult condition we will do a basic calculation for understanding purpose.

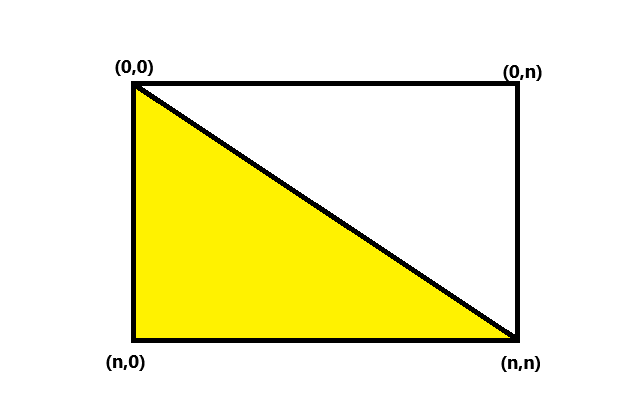
in this we can see that we are trying to make a lower triangular we will see how we can build the logic for it .We all know how to calculate the equation of a straight line. The formula for this is (x-x1)/(x2-x1)=(y-y1)/(y2-y1) we will simply put the coordinates of the point (0,0) and(n,n) in this equation .
So we get a format like this : (i-0)/(n-0) = (j-0)/(n-0)
\=> i=j.
now as we can see we are try to fill the space towards coordinate (n,0)we will put the value in the evaluated solution as we can see n>0 so we can say that i>=j
lets Implement this solution.

n = int(input("Enter an odd integer: "))
if n % 2 == 0:
    print("Input must be an odd integer")
else:
    for i in range(n):
        for j in range(n):
            if(i>=j): #We will change only this segment only for the rest of the part
                print("*", end=" ")
            else:
                print(" ", end=" ")
        print()
#Output:-
*
* *
* * *
* * * *
* * * * *

Similarly, we can find the upper triangular matrix.
We know how to calculate the equation of a straight line. The formula is (x-x1)/(x2-x1)=(y-y1)/(y2-y1). We simply use the coordinates of the points (0,0) and (n,n) in this equation.
This gives us: (i-0)/(n-0) = (j-0)/(n-0)
\=> i = j.
Now, as we try to fill the space towards the coordinate (0,n), we use the evaluated solution. Since n > 0, we can say that i <= j.

Let's implement this solution.

n = int(input("Enter an odd integer: "))
if n % 2 == 0:
    print("Input must be an odd integer")
else:
    for i in range(n):
        for j in range(n):
            if(i<=j): #We will change only this segment only for the rest of the part
                print("*", end=" ")
            else:
                print(" ", end=" ")
        print()
#Output:-
* * * * *
  * * * *
    * * *
      * *
        *

We can also Solve the complex pattern like Diamond shape problem

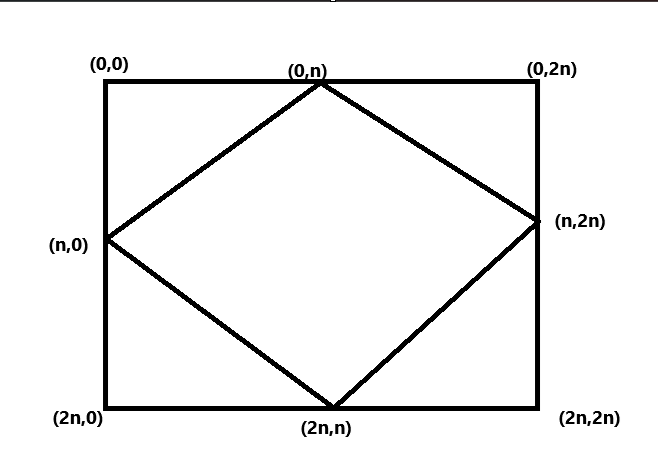
Here, we can similarly find the upper triangular matrix. We know how to calculate the equation of a straight line. The formula is (x-x1)/(x2-x1) = (y-y1)/(y2-y1). We simply use the coordinates of the points in this equation.

1. (0, n), (n, 0)

2. (n, 0), (2n, n)

3. (2n, n), (n, 2n)

4. (0, n), (n, 2n)

   Now, as we can see, we are trying to fill the space towards the coordinate (2n, 2n) for line 2, and (0, 2n) for line 3. For line 4, the points are (0, 0) and (2n, 0). So, we will use these points in the evaluated solution. Since n > 0, we can say that i >= j.

   Let's implement this solution.

We will get the equations as follows:

1. i + j >= n

2. j - i <= n

3. i - j <= n

4. i + j <= 3 * n

n= int(input("Enter the number"))
for i in range(2*n+1):
  for j in range(2*n+1):
    if(i+j>=n and j-i<=n and i-j<=n and i+j<=3*n ):
      print("*",end=" ")
    else:
       print(" ",end=" ")
  print(" ")
#Output:-
          *            
        * * *          
      * * * * *        
    * * * * * * *      
  * * * * * * * * *    
* * * * * * * * * * *  
  * * * * * * * * *    
    * * * * * * *      
      * * * * *        
        * * *          
          *

By using this basic formula, we can easily solve different types of pattern problems.