Deleting the Middle Node of a Linked List Using the Tortoise and Hare Algorithm in TypeScript
 Enoch Olutunmida
Enoch Olutunmida
Introduction
In this post, we’ll be solving LeetCode Problem 2095: “Delete the Middle Node of a Linked List.”
The problem statement on LeetCode is:
You are given the head of a linked list. Delete the middle node and return the head of the modified linked list.
In essence, our goal is to remove the middle node from a singly linked list using an efficient approach that finds the middle without traversing the list multiple times.
To solve it, we’ll employ the Tortoise and Hare (Two-Pointer) algorithm, a technique commonly used for linked list problems involving a slow and a fast pointer. This blog covers the code, essential edge cases, and explains how the two-pointer logic works visually.
If you would prefer a video walkthrough, check out my YouTube video here, where I explain the solution step-by-step!
Problem Breakdown
The task requires us to:
Traverse the linked list to locate the middle node.
Remove this middle node without needing to re-traverse the entire list.
Constraints: The linked list will have at least one node.
To tackle this efficiently, we’ll rely on two pointers:
Fast Pointer (Hare): Moves two steps at a time.
Slow Pointer (Tortoise): Moves one step at a time.
When the fast pointer reaches the end of the list, the slow pointer will be at the middle node.
Step-by-Step Solution Using the Tortoise and Hare Algorithm
Step 1: Initialise Pointers
We initialise:
slowPointerandfastPointerboth pointing to the head of the linked list.prevPointerasnull, to keep track of the node before the slow pointer.
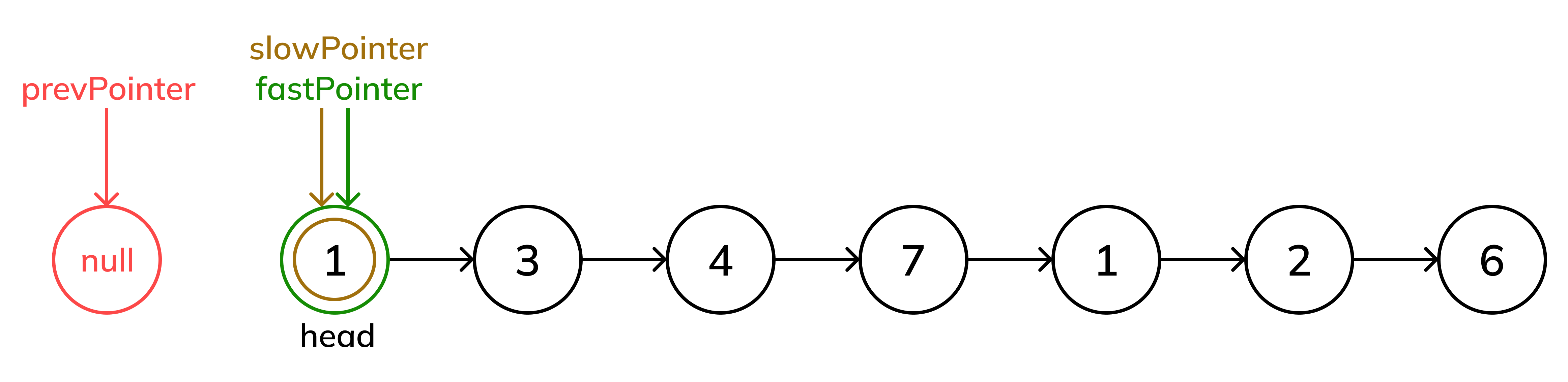
Step 2: Traverse the List
With each iteration:
Update
prevPointerto point to the currentslowPointerbefore it moves forward.Move
slowPointerone step forward.Move
fastPointertwo steps forward.
This setup ensures that by the time fastPointer reaches the end of the list, slowPointer will be at the middle node, and prevPointer will be one step behind it.
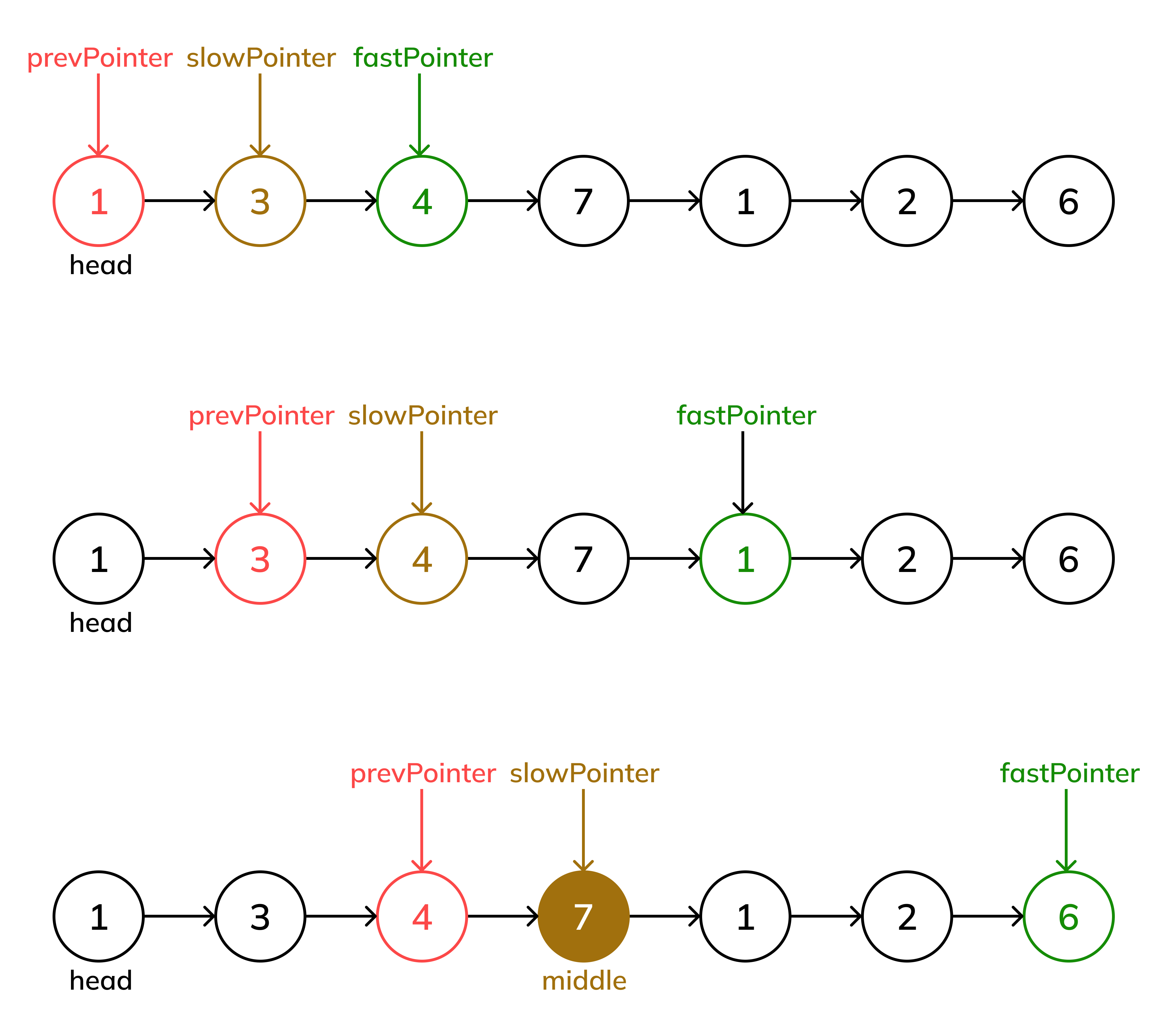
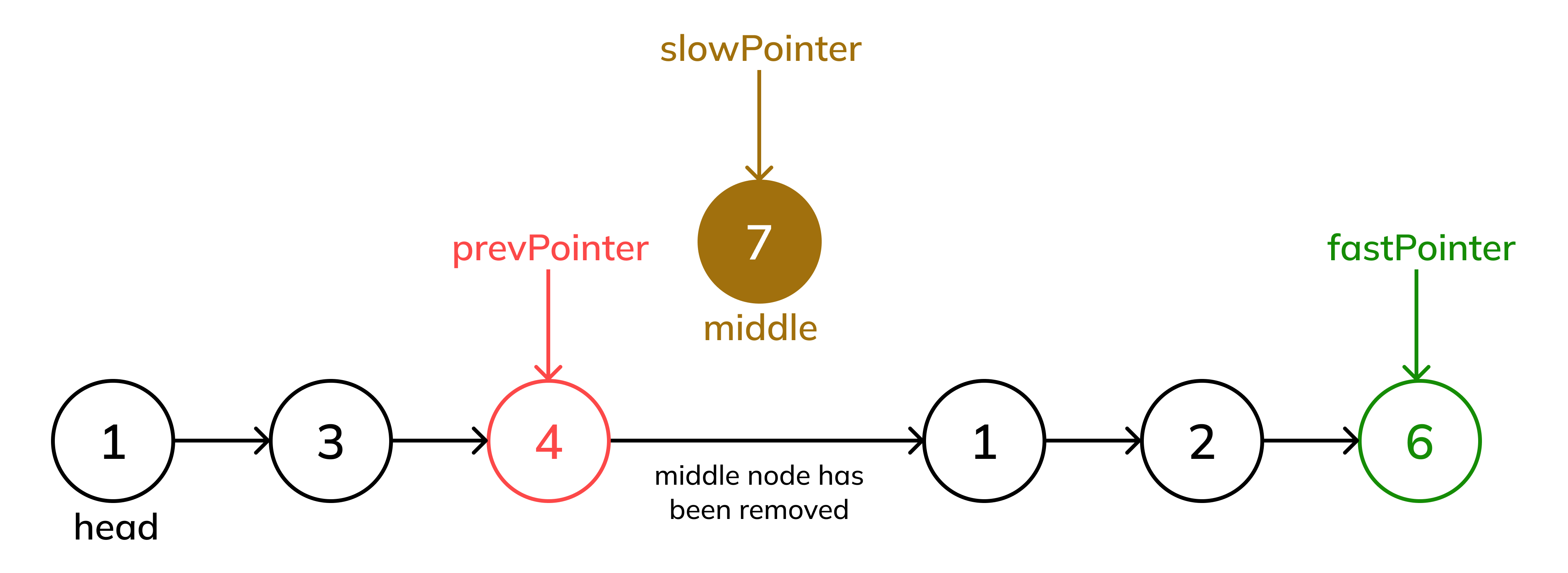
Step 3: Remove the Middle Node
Once the traversal is complete:
Confirm that
slowPointeris at the middle node.Adjust Pointers: Set
prevPointer.next = slowPointer.nextto "skip" the middle node (the oneslowPointeris currently pointing to), effectively deleting it from the list.
Step 4: Edge Case - Single Node List
If the list has only one node, fastPointer won’t be able to move two steps. In this case:
- Simply return
nullas removing the middle node from a single-node list leaves the list empty.
Code Implementation in TypeScript
Here’s how the solution looks in TypeScript:
function deleteMiddle(head: ListNode | null): ListNode | null {
if (!head.next) {
return null;
}
let slowPointer = head;
let fastPointer = head;
let prevPointer = null;
while (fastPointer && fastPointer.next) {
prevPointer = slowPointer;
slowPointer = slowPointer.next;
fastPointer = fastPointer.next.next;
}
if (prevPointer) {
prevPointer.next = slowPointer.next;
}
return head;
};
Explanation of the Code
Edge Case Handling: The first check ensures that if the list has only one node (or none), it returns
null.Traversing the List: The
whileloop movesfastPointerby two steps andslowPointerby one step. At the same time,prevPointerupdates to stay one step behindslowPointer.Node Deletion: After the loop,
prevPointer.nextis set toslowPointer.next, effectively removing the middle node from the list.
Complexity Analysis
Time Complexity: O(n) because we’re traversing the list with the two pointers just once.
Space Complexity: O(1) as no additional space is used beyond the three pointers.
Edge Cases and Additional Considerations
Single Node List: As mentioned, returning
nullwhen there’s only one node in the list.Two Node List: After removing the middle node, the list should contain just one node.
Odd vs. Even Length Lists: For an odd-length list, the exact middle node is removed. For an even-length list, the second of the two central nodes is considered the middle.
Conclusion
The Tortoise and Hare algorithm provides an efficient solution to this problem by requiring only a single traversal to locate and delete the middle node. This approach is also valuable for other linked list problems, such as detecting cycles or identifying the start of a loop.
Mastering this algorithm will deepen your understanding of linked list problem-solving, a skill that often proves valuable in coding interviews.
Subscribe to my newsletter
Read articles from Enoch Olutunmida directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by

Enoch Olutunmida
Enoch Olutunmida
I’m Enoch, a Software Engineer with 7+ years of experience building fintech solutions, mobile games, and blockchain applications. I’m passionate about innovation and solving complex problems, and I love to architect systems and streamline processes that drive continuous improvement.