Introduction to NumPy

NumPy, short for Numerical Python, is a foundational Python library essential for numerical and scientific computing. It introduces a powerful data structure, the array, which is more efficient than Python lists for handling large datasets and performing mathematical operations. The efficiency of NumPy makes it a core component in data science workflows, from data manipulation and preprocessing to advanced machine learning tasks, as many data science libraries, such as Pandas and SciPy, are built on top of or heavily integrated with NumPy.

Overview of the NumPy Random Module

The numpy.random module in Python is a part of the NumPy library specialising in generating random numbers, creating random samples, and working with statistical distributions. This module is a go-to for data scientists who must incorporate randomness or generate datasets based on specific statistical properties. It offers a wide range of applications like generating random numbers, generating different probability distributions, generating random permutation and ensuring reproducibility with random seeds.

Key Functions

1. Generating Random Number

numpy.random.rand()

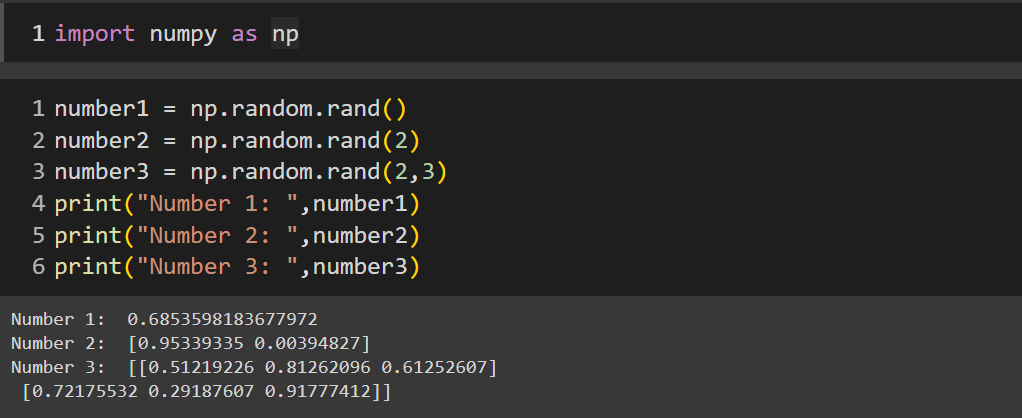
• numpy.random.rand() will return a random float number (positive number) in the desired shape. It can generate a single number, two numbers and an array and the numbers are getting picked from the uniform distribution from 0 to 1.

numpy.random.randint()

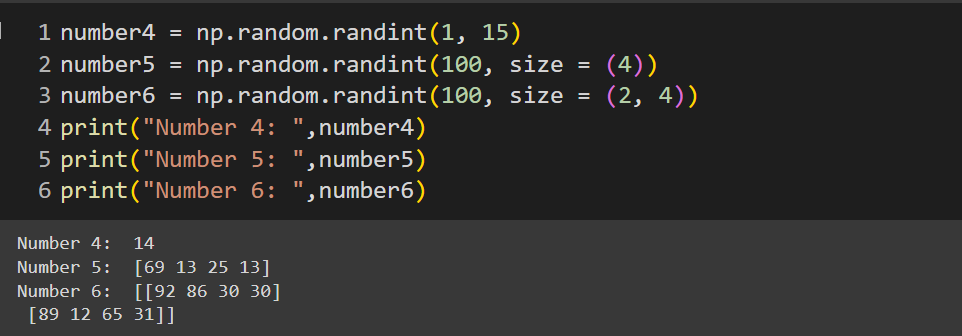
• numpy.random.randint(low,high,size) function will take a low and high argument & return random integers from the half-open interval. i.e [low, high) == low(inclusive), high (exclusive). The size of the array can be mentioned in the size argument.

numpy.random.randn()

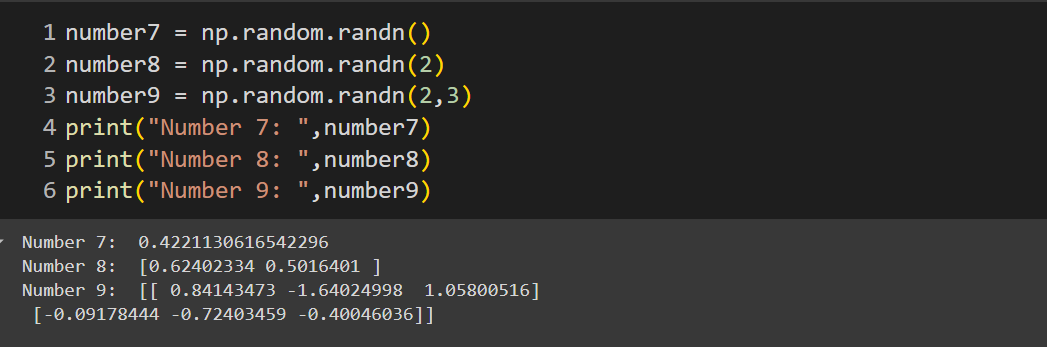
• numpy.random.randn() will return a random float number (both positive and negative numbers) in the desired shape. It can generate a single number, two numbers and an array. The numbers are picked from the standard normal distribution from 0 to 1.

numpy.random.choice()

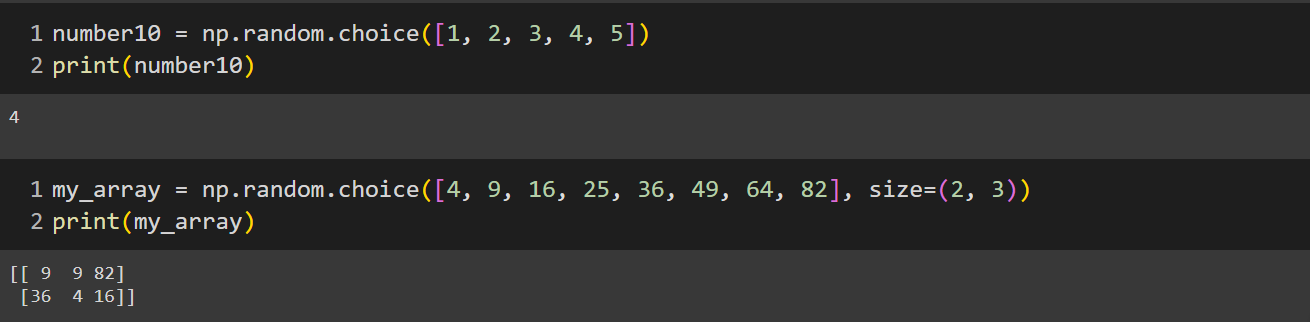
• The function generates a random sample from a given 1-D array or we can use this size argument to generate the sample size of our choice

2. Generating Random Permutation

numpy.random.permutation() and numpy.random.shuffle()

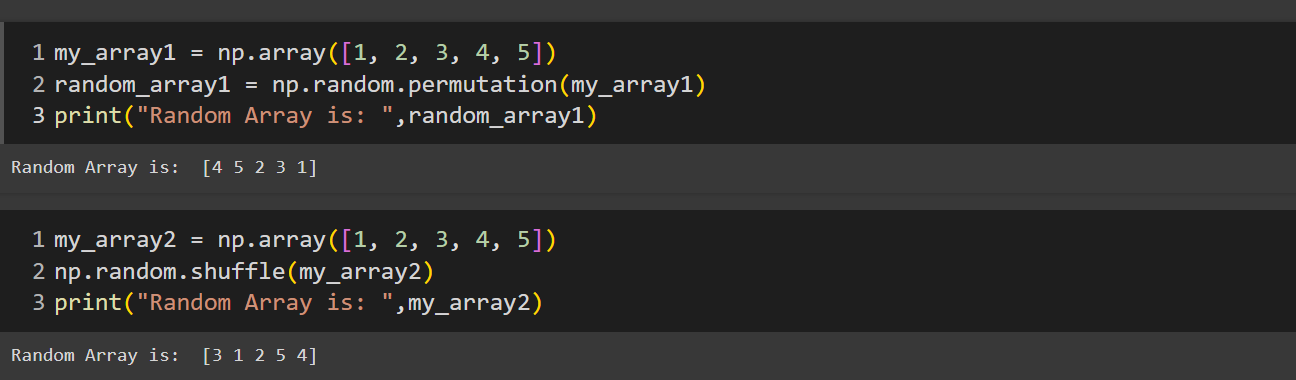
• numpy.random.permutation() function produces a new array which results in a shuffled version of the my_array. It doesn't modify the original array rather it produces a randomized order of the elements.

• numpy.random.shuffle() function shuffle the items of my_array2 without creating a new array.

• shuffling and permutation is useful for applications like andomizing sequences, or creating randomized indices for sampling.

3. Probability Distribution

numpy.random.normal()

import numpy as np
import seaborn as sns

n = np.random.normal(loc = 0.0, scale = 3.0, size = 1000)
sns.histplot(n, kde=True)

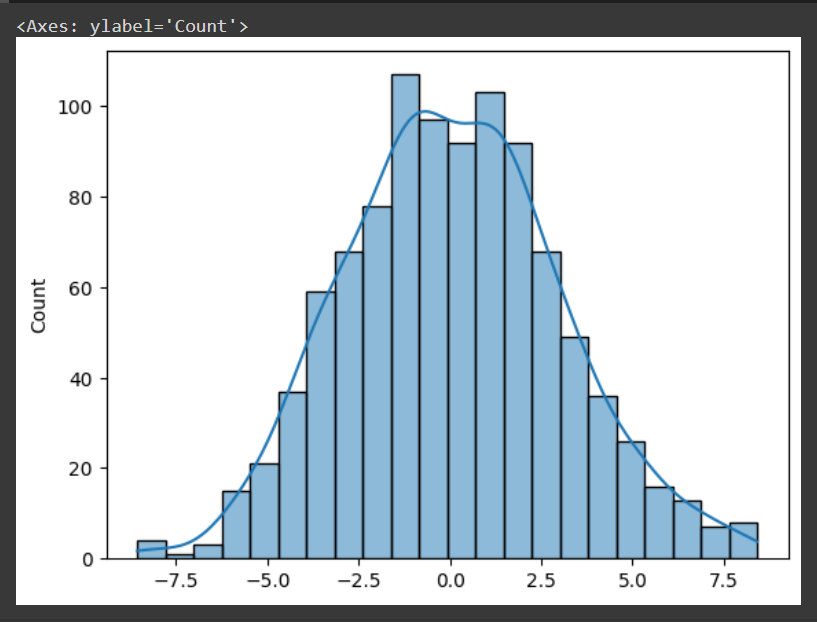
• This function generates random numbers that follow a normal distribution characterized by a mean denoted by loc, standard deviation denoted by scale and size ie the number of points. If size is not specified then a a single value is returned.

• The normal distribution or the Gaussian distribution is a fundamental probability distribution that appears in numerous natural phenomena. Mean is the distribution's center or average value and the standard deviation is the spread or width of the distribution.

• In the above code, we have generated 1000 points which follow gaussian distribution and plotted these points using seaborn. You can in the plot that the points are following a nice gaussian curve.

numpy.random.binomial()

• This function generates random numbers that follow a binomial distribution characterized by an n ie number of trails, p ie probability for each trail and size ie shape of the output array. If size is not specified then a single random value representing the number of successes is returned.

numpy.random.uniform()

u = np.random.uniform(low = 1, high = 10, size = 200)
sns.histplot(u)

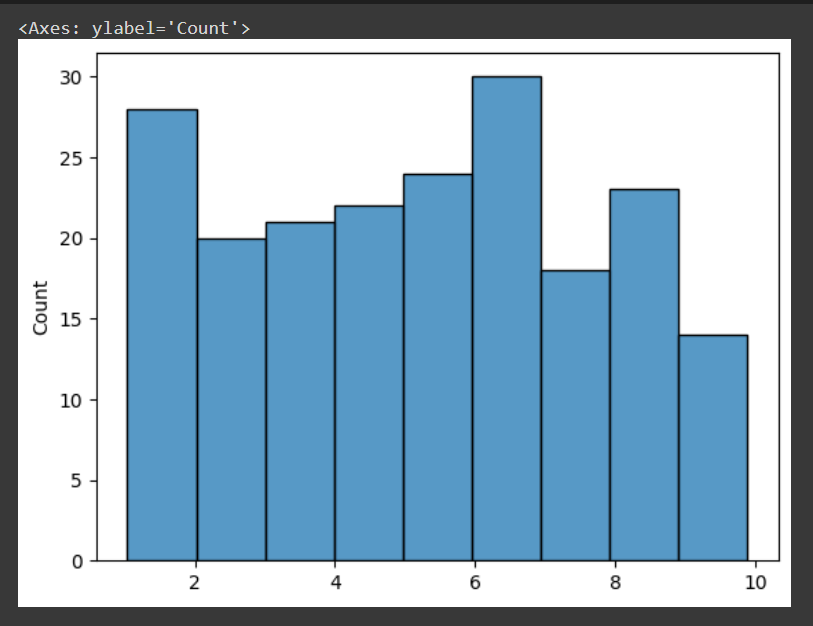
• This function generates random numbers that follow a uniform distribution distribution within the specified range [low, high). A probability distribution known as the uniform distribution gives each value within a range an equal chance of happening.

• The argument of the function is characterized by a low ie the lower boundary of the range, and a high ie the upper boundary and size ie the shape of the output array. If size is not specified, a single random value within the range is returned.

• In the above code, we have generated 200 points where the low value is 1 and the high value is 10 and it follows a uniform distribution. You can in the plot that the points are following uniform distribution.

4. Reproducibility with Random Seeds

numpy.random.seed()

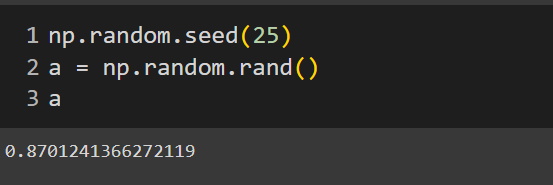
• This method is used when we want to reproduce the same number every time we run the code. We can initialize the seed by giving any random integer to generate a random set of numbers, and with the same seed value, a similar set of numbers will be generated every time.

Importance of Random Number Generation in Data Science

Random number generation plays a crucial role in data science for a variety of applications:

1. Simulations and Modeling: Random numbers are essential for simulations in fields like finance, engineering, and healthcare. For instance, random number generation can model stock price movements or interest rate fluctuations in financial simulations.

2. Randomness in Algorithms: Many machine learning algorithms rely on random numbers to initialize parameters or shuffle data. For example, algorithms like stochastic gradient descent (SGD) use random initializations to avoid local minima, improving model training and convergence.

3. Data Augmentation and Synthetic Data Generation: Random numbers help create synthetic datasets, which can supplement limited data or augment existing data for model robustness. Generating random samples allows for diverse scenarios, making models more generalizable to unseen data.

4. Data Preprocessing

   • Shuffling Data: Data shuffling is essential to prevent the model from learning order patterns in data that don't generalize well. The numpy.random.shuffle() function is often used to randomize the order of dataset rows.

     • Example: Shuffling a dataset before training helps avoid bias in models, especially when data is initially sorted by class.

   • Train-Test Splitting: A critical step in model evaluation, splitting data into training and test sets is commonly randomized to ensure that each subset accurately represents the overall dataset. Using numpy.random.choice() for sampling can help create these subsets while maintaining randomness.

By leveraging random numbers, data scientists can conduct robust testing, prevent overfitting, and simulate complex phenomena, making random number generation an indispensable tool.

Performance Considerations

The numpy.random module offers significant performance advantages over Python’s built-in random module, primarily because of NumPy’s underlying design that leverages vectorized operations and optimized C code. This means it can generate large arrays of random numbers far more efficiently than the standard library, making it ideal for data science tasks that require substantial random data generation, such as simulations or large-scale Monte Carlo experiments. The built-in random module is sufficient for smaller, simpler tasks, numpy.random shines in tasks needing high computational efficiency due to its ability to operate on arrays rather than individual elements. This capability not only reduces the execution time but also minimizes memory usage by avoiding Python’s interpreter overhead.

References

• https://mrexamples.com/python/numpy/numpy-random/

• https://numpy.org/doc/1.16/reference/routines.random.html

• https://numpy.org/doc/stable/