Data-Level Parallelism (DLP) refers to the parallel execution of identical operations on different elements of a data set, allowing for a significant increase in computational speed and efficiency. This type of parallelism is particularly well-suited for applications that involve repetitive operations on large volumes of data, such as matrix operations in scientific computing, image processing, and audio processing. By utilizing architectures that support DLP, such as SIMD (Single Instruction, Multiple Data), a single instruction can be used to operate on multiple data elements concurrently, significantly reducing execution time compared to processing each data element sequentially. As the need for processing large data sets grows in modern computing, the ability to exploit DLP becomes increasingly essential in achieving optimal performance.

Introduction to SIMD Architecture

SIMD is a type of parallel architecture where a single instruction can perform operations on multiple data points simultaneously. It is especially useful in applications that have high data-level parallelism (DLP), such as scientific computing, image and sound processing. The potential energy efficiency of SIMD, compared to Multiple Instruction, Multiple Data (MIMD), makes it attractive for Personal Mobile Devices. The main advantage of SIMD over MIMD is its simplicity for the programmer, as it provides parallelism in data operations while retaining a sequential execution model.

Variations of SIMD

The chapter discusses three variations of SIMD:

Vector Architectures: These architectures predate the other variations by 30 years and involve essentially pipelined execution of many data operations. They were considered too costly for microprocessors until recently due to the expense of transistors and the need for significant DRAM bandwidth.
Multimedia SIMD Instruction Set Extensions: These are found in many modern instruction sets like x86 and support multimedia applications. Examples include MMX (Multimedia Extensions) and SSE (Streaming SIMD Extensions), followed by AVX (Advanced Vector Extensions).
Graphics Processing Units (GPUs): GPUs share similarities with vector architectures but evolved differently due to their unique ecosystem. They offer higher potential performance and are often referred to as heterogeneous architectures due to their combination of system processors and dedicated graphics memory.

All three variations provide a simpler path to achieving parallelism for certain problems, compared to MIMD. The chapter highlights the potential speedup and performance gains expected from SIMD, with an emphasis on how important it is to understand SIMD, given the growth in both data-level parallelism and Thread-Level Parallelism (TLP).

Vector Architecture

Vector Architectures are efficient for executing vectorizable applications. These architectures collect sets of data elements from memory, place them into large, sequential register files, operate on them, and then store the results back into memory. Each vector instruction handles a vector of data, resulting in several register operations on independent data elements, which is particularly efficient for DLP.

Key aspects of vector architectures:

They use large compiler-controlled register files to minimize memory latency and leverage memory bandwidth.
Since loads and stores are deeply pipelined, latency is amortized over large vectors, keeping the execution units busy.
The vector processor discussed in the chapter is called VMIPS, which is loosely based on the Cray-1 supercomputer. VMIPS includes:
- Vector Registers: Each vector register is fixed-length and holds multiple elements. VMIPS has eight vector registers, each with 64 elements.
- Vector Functional Units: Each is fully pipelined, supporting new operations every clock cycle.
- Vector Load/Store Unit: Handles loading and storing vectors to and from memory.
- Scalar Registers: The normal MIPS general-purpose and floating-point registers, providing input to vector functional units and computing addresses for vector memory operations.

Vector Instructions in VMIPS use the same names as scalar MIPS instructions, with the suffix "VV" to denote operations on vectors (e.g., ADDVV.D for vector addition). There are also mixed operations involving vectors and scalars, indicated by "VS" (e.g., ADDVS.D).

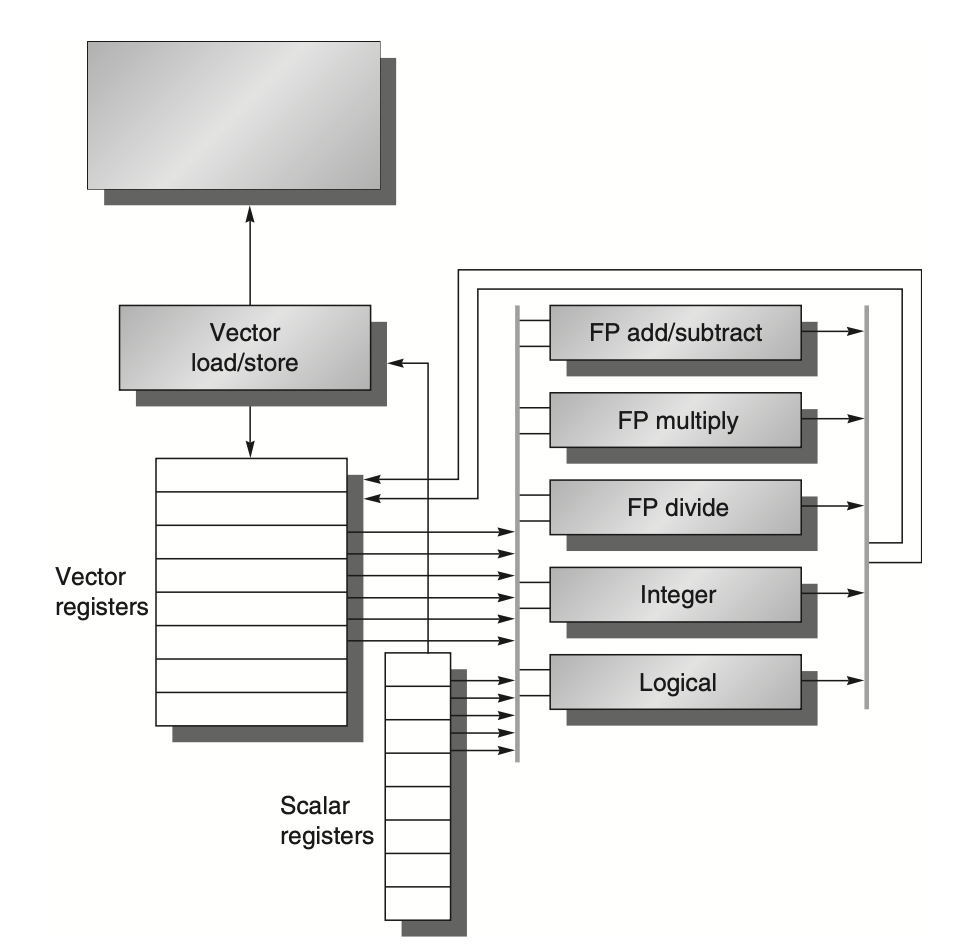
Figure: The VMIPS architecture, based on MIPS, features a scalar design along with vector processing capabilities. It includes eight vector registers, each capable of holding 64 elements, and all functional units are specialized for vector operations. The VMIPS processor provides vector instructions for both arithmetic and memory operations, allowing it to behave like a typical vector processor while also supporting logical and integer operations. Although these logical units are usually part of a standard vector processor, they are not the focus here. The vector and scalar registers are designed with a significant number of read and write ports, enabling multiple vector operations to run concurrently. These ports are connected to the vector functional units via crossbar switches, which facilitate efficient data flow between registers and functional units.

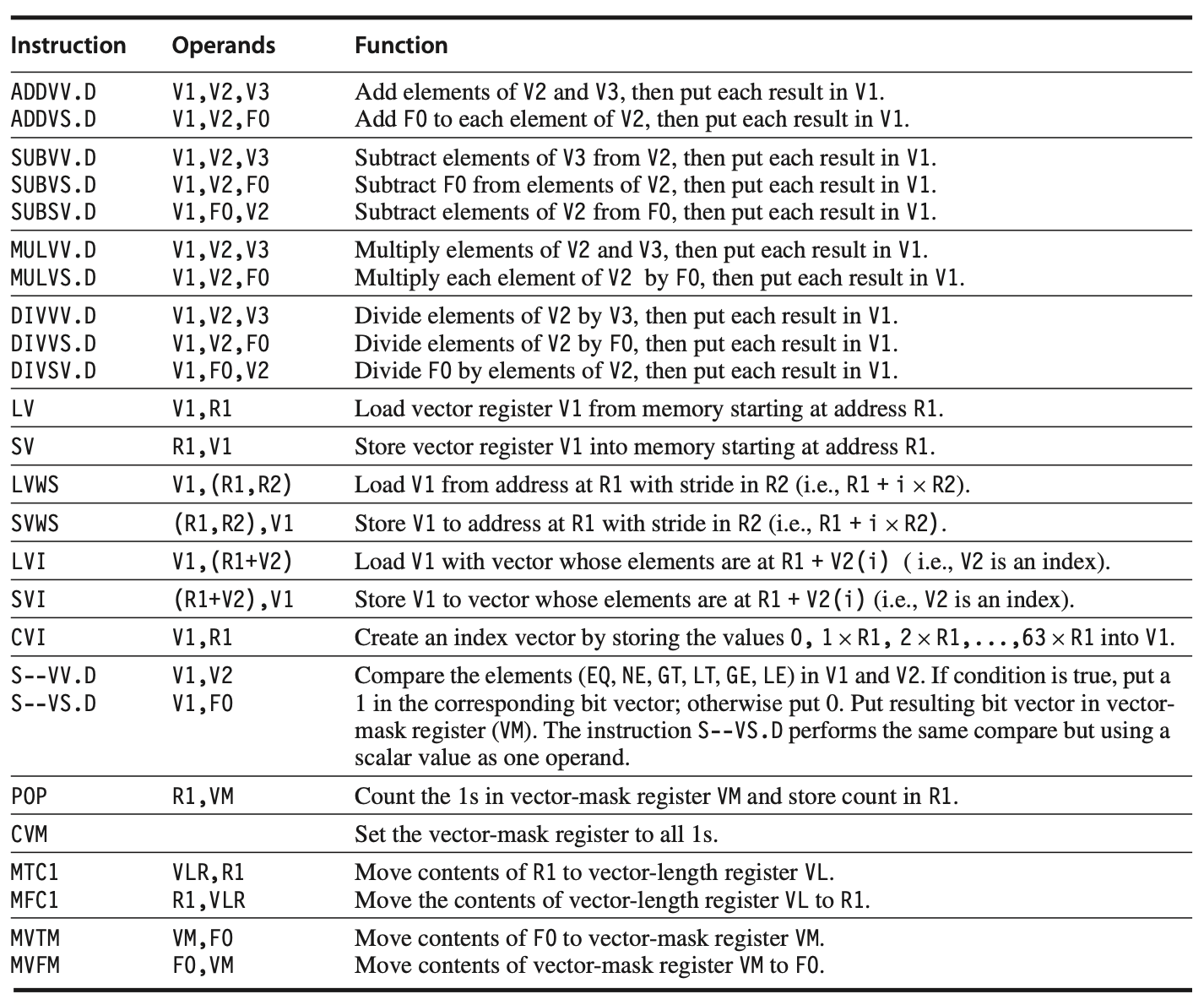
Figure: The VMIPS vector instructions include double-precision floating-point operations, supported by vector registers along with two special registers: VLR and VM. These special registers reside in the coprocessor 1 space of the MIPS architecture, alongside the floating-point unit (FPU) registers. Additionally, VMIPS supports operations involving stride, index creation, and indexed load/store.

Power Efficiency and Flexibility of Vector Instructions

Vector instructions are efficient due to their capability to operate on many elements simultaneously. This allows architects to use slower but wider execution units to achieve high performance without high power demands. The flexibility of vector designs makes them useful for both scientific applications and multimedia tasks. By allowing varying data sizes (e.g., 64-bit, 32-bit, 16-bit, 8-bit), vector architectures can adapt to different hardware requirements effectively.

The chapter suggests that understanding the basics of SIMD, especially vector and GPU architectures, is crucial for maximizing the benefits of data-level parallelism while balancing complexity and power efficiency. The detailed analysis of VMIPS also offers insights into how vector instructions are designed to improve performance without the added complexity of out-of-order superscalar processors.

This content sets the stage for deeper exploration of SIMD and vector processing, focusing on maximizing parallelism, managing memory bandwidth, and understanding the trade-offs involved in modern processor design.

How VMIPS works

To understand how vector processors work, let’s consider an example involving a vector loop for the VMIPS processor. This example is a typical vector problem, which we will reference throughout the section:

Y = a × X + Y

Here, X and Y are vectors initially residing in memory, and 'a' is a scalar value. This operation is commonly known as SAXPY (Single-Precision a × X plus Y) or DAXPY (Double-Precision a × X plus Y). It forms the core operation of the Linpack benchmark, which is a set of linear algebra routines used for measuring computer performance, particularly for solving systems of linear equations.

Assuming that the number of elements (the vector length) matches the length of the vector register, we can illustrate the execution with a simplified VMIPS implementation.

MIPS Code for DAXPY

The MIPS implementation of DAXPY involves loading the scalar and individual elements from the vectors X and Y, performing the arithmetic operation, and then storing the result. The following is the MIPS code for DAXPY:

L.D   F0, a         ; load scalar a
DADDIU R4, Rx, #512 ; last address to load
Loop: L.D   F2, 0(Rx)  ; load X[i]
      MUL.D F2, F2, F0 ; a × X[i]
      L.D   F4, 0(Ry)  ; load Y[i]
      ADD.D F4, F4, F2 ; a × X[i] + Y[i]
      S.D   F4, 0(Ry)  ; store into Y[i]
      DADDIU Rx, Rx, #8 ; increment index to X
      DADDIU Ry, Ry, #8 ; increment index to Y
      DSUBU R20, R4, Rx ; compute bound
      BNEZ  R20, Loop   ; check if done

In the above code, the instructions execute in a loop, processing one element of X and Y at a time. The loop involves multiple load and store instructions, which introduce significant overhead and make this code less efficient for a long vector length.

VMIPS Code for DAXPY

In contrast, the VMIPS implementation uses vector instructions that allow operations on entire vectors in one go, greatly reducing the number of instructions needed and minimizing overhead. Here’s the VMIPS code for the DAXPY operation:

L.D      F0, a      ; load scalar a
LV       V1, Rx     ; load vector X
MULVS.D  V2, V1, F0 ; vector-scalar multiply
LV       V3, Ry     ; load vector Y
ADDVV.D  V4, V2, V3 ; vector addition
SV       V4, Ry     ; store the result

The VMIPS code executes the entire DAXPY operation using only 6 instructions, as compared to almost 600 iterations required for MIPS. This is because vector operations like LV (Load Vector) and SV (Store Vector) operate on entire vector registers containing multiple elements (e.g., 64 elements). As a result, the overhead associated with multiple iterations and scalar load/store instructions is greatly reduced.

The concept of vectorization comes into play when the compiler converts scalar instructions into vector instructions, enabling the execution of multiple operations in parallel. The resulting code is said to be vectorized. Loops that can be vectorized generally do not have dependencies between iterations, known as loop-carried dependencies.

A significant difference between MIPS and VMIPS is the frequency of pipeline interlocks. In MIPS, each instruction must wait for the previous one to complete before it can proceed. For example, every ADD.D must wait for the preceding MUL.D to finish, and every S.D must wait for ADD.D. In a vector processor, however, each instruction only stalls for the first element in the vector, and subsequent elements continue flowing through the pipeline without waiting. This mechanism is called chaining, where dependent operations are "forwarded" to the next functional unit as soon as they become available.

In VMIPS, pipeline stalls occur only once per vector instruction, rather than once per element. For instance, in the DAXPY example, MULVS.D and ADDVV.D are chained, meaning the output from the multiply operation is immediately used as input to the addition without waiting for the entire vector to complete.

The execution time for a vector sequence depends on the vector length, structural hazards, and data dependencies. A useful concept here is a convoy, which is a set of vector instructions that can be executed together. The time taken to execute a convoy is known as a chime. For example, if a vector sequence consists of m convoys and the vector length is n, then the total execution time in chimes for VMIPS would be approximately m × n clock cycles.

Chaining allows vector operations to start as soon as individual elements of its source operand are ready. Early implementations of chaining worked like forwarding in scalar pipelines, but recent implementations use flexible chaining, which allows chaining to occur between any active vector instructions, assuming no structural hazards exist. This flexibility is supported by modern vector architectures, which improves performance and reduces stalls.

Multiple Lanes: Beyond One Element per Clock Cycle: A key advantage of a vector instruction set is its ability to perform many operations in parallel using a single instruction. Multiple lanes add further parallelism by dividing vector functional units into separate pipelines, allowing multiple elements to be processed simultaneously. In VMIPS, each lane handles a portion of the vector register, enabling operations on different elements concurrently. Adding more lanes increases throughput without significant control complexity or changes to machine code. This approach allows vector processors to achieve higher performance while managing energy consumption and hardware complexity efficiently.

Vector-Length Registers: Handling Loops Not Equal to 64: A vector-length register (VLR) allows vector operations to handle loops where the vector length may not be equal to the register length, such as when the length is less than or equal to the maximum vector length (MVL). If the vector length exceeds the MVL, a technique called strip mining is used. Strip mining divides the vector into segments that match the MVL, enabling efficient processing by iterating over these segments in a series of loops. This approach ensures that vector operations can handle arbitrary lengths effectively without exceeding the available register capacity.

Vector Mask Registers: Handling IF Statements in Vector Loops: Vector-mask registers enable vector processors to handle conditional statements in loops by providing a way to execute vector operations selectively. In cases where an IF condition is present, vector-mask control uses a Boolean vector to determine which elements should be processed. This allows vector operations to execute only for elements that satisfy the condition, improving vectorization in loops with conditional dependencies. Although using vector-mask registers can add overhead, they often provide significant performance benefits over scalar execution.

Memory Banks: Supplying Bandwidth for Vector Load/Store Units: The behavior of vector load/store units is more complex compared to arithmetic units due to the need for high bandwidth from memory. Start-up penalties for load/store units are high, often requiring many clock cycles, such as 12 cycles for VMIPS. To maintain efficient data flow, vector processors use multiple independent memory banks, allowing simultaneous memory accesses and reducing stalls. This approach supports multiple loads/stores per clock cycle, non-sequential data accesses, and independent address streams for shared memory systems, ensuring sufficient bandwidth to meet processor demands.

Stride: Handling Multidimensional Arrays in Vector Architectures: In vector architectures, handling multidimensional arrays requires the concept of stride to access non-sequential memory locations efficiently. Stride refers to the distance between adjacent elements in memory. For example, accessing matrix elements in row-major or column-major order often involves non-unit strides. Vector processors can use special load and store instructions with stride to handle such cases, making them effective for multidimensional data processing without requiring contiguous memory. However, supporting non-unit strides complicates memory management, as it can lead to memory bank conflicts and reduced throughput.

Gather-Scatter: Handling Sparse Matrices in Vector Architectures: The gather-scatter technique is used to handle sparse matrices in vector architectures. Gather operations use an index vector to fetch elements from memory, storing them in a dense form in a vector register. After processing, scatter operations write these elements back to their original sparse form. This approach allows sparse matrix operations to run in vector mode efficiently, using indexed vector instructions. Although these operations have higher latency compared to non-indexed loads/stores due to unpredictable memory access patterns, they provide flexibility in handling sparse data structures in vector processing.

Programming Vector Architectures: Vector architectures allow compilers to inform programmers during compile time whether code will be vectorized, often providing hints for improvements. The success of vectorizing a program largely depends on its structure, particularly data dependencies within loops. By giving hints to the compiler, programmers can significantly increase vectorization levels, as demonstrated in studies comparing initial code with hint-optimized versions, which showed improvements from around 70% to 90% vectorization.

What is SIMD?

SIMD started with a simple idea: many media applications operate on narrower data types than the traditional 32-bit processors were originally optimized for. For example, many graphics systems use 8 bits to represent each of the three primary colors plus an additional 8 bits for transparency, and audio samples might be 8 or 16 bits. By partitioning the data and performing simultaneous operations on several smaller operands, SIMD can effectively boost processing speed for these multimedia workloads.

Imagine a 256-bit adder that can operate on 32 different 8-bit values at the same time—this is the power of SIMD. It takes what could be a very serial process and makes it parallel, significantly boosting performance for tasks like image and audio processing.

SIMD instructions act like vector instructions, processing a set of data in parallel. But unlike full-fledged vector machines with extensive register files (like the VMIPS vector processor that holds up to sixty-four 64-bit elements in each of its 8 vector registers), SIMD instructions are typically designed to handle fewer operands, which means the register files are smaller and more lightweight.

SIMD vs. Vector Machines

SIMD instructions and vector machines are cousins in the processor family tree, but they have some important differences. Vector machines have powerful variable-length registers and sophisticated addressing modes, allowing them to easily handle complex data structures like strided arrays or gather-scatter operations. SIMD, on the other hand, has a more straightforward design with a fixed number of operands.

While this makes SIMD less flexible, it also means that it's easier to integrate into existing processor designs, especially for multimedia extensions like MMX, SSE, and AVX—extensions that you've likely heard of in modern x86 architectures. This fixed length is one reason SIMD was adopted so widely in consumer-grade CPUs for multimedia tasks.

How SIMD Has Evolved

The first major SIMD extension was MMX, introduced by Intel in 1996. MMX reused existing floating-point registers to perform multiple integer operations in parallel, but it was limited to working with 64-bit registers. Later, in 1999, SSE (Streaming SIMD Extensions) came along with dedicated 128-bit registers, allowing for more simultaneous operations. Over the years, Intel released SSE2, SSE3, and SSE4, with each generation enhancing support for floating-point and integer operations.

In 2010, the AVX (Advanced Vector Extensions) was introduced, doubling the register size to 256 bits and further increasing the ability to process data in parallel. Each evolution has been about increasing the ability to perform simultaneous operations, whether that means handling more data at once or being able to do more complex operations.

But SIMD isn't without its drawbacks. Unlike vector machines, SIMD lacks some features that would make it easier for compilers to generate efficient code automatically. For example:

SIMD uses a fixed-length register size, which limits its flexibility compared to variable-length vector registers.
SIMD doesn't support complex addressing modes like gather-scatter operations that are common in scientific computing.
SIMD often lacks mask registers, which limits its ability to handle conditional operations.

These limitations mean that programming with SIMD is often done manually in assembly language or with carefully optimized libraries, rather than relying on compilers to automatically generate SIMD instructions from high-level code.

Why SIMD is Still Popular

Despite these challenges, SIMD extensions have become a mainstay of multimedia processing for several reasons:

Low Cost: The hardware requirements for SIMD are minimal compared to a full vector processing unit, making it an affordable addition to CPUs.
Small Register Footprint: SIMD uses shorter fixed-length registers, which are easier to manage in general-purpose CPUs, especially during context switching.
Avoiding Virtual Memory Issues: SIMD doesn’t run into the same virtual memory problems as vector processors do. Since SIMD instructions operate on smaller data sets, they are less likely to hit page faults in the middle of a vector operation.
Cache Compatibility: SIMD works effectively with existing CPU cache architectures, whereas traditional vector processors often needed specialized cache handling.

These reasons make SIMD an ideal choice for enhancing the multimedia capabilities of modern CPUs without needing to fundamentally change how processors are designed or how memory is accessed.

A Real-World Example: SIMD in MIPS

To illustrate how SIMD instructions work, consider an example where 256-bit SIMD multimedia instructions are added to the MIPS instruction set. In this example, the goal is to handle floating-point operations, with each SIMD instruction working on four double-precision operands simultaneously. This way, instead of sequentially processing one value at a time, SIMD allows for processing multiple values with a single instruction, significantly boosting efficiency.

The SIMD instructions for MIPS, such as L.4D (load four double-precision values), replace the traditional double-precision MIPS operations with new SIMD operations, resulting in fewer dynamic instructions executed—a reduction from 578 to just 149 in this specific case. That’s the magic of SIMD: fewer instructions, more parallelism, and much greater efficiency.

The Roofline Model: Evaluating SIMD Performance

To understand SIMD's effectiveness, we can use the Roofline Model, which visualizes the interplay between memory bandwidth and computational power. The Roofline sets an upper bound on achievable performance based on two factors: the processor's peak floating-point performance and its memory bandwidth.

The Roofline graph has a horizontal line that represents peak floating-point performance and a diagonal line that represents memory bandwidth. The performance of any workload will be bound by either the flat roof (computation-limited) or the slanted roof (memory bandwidth-limited), depending on the arithmetic intensity of the program. For processors with high memory bandwidth, the “ridge point”—where the diagonal and horizontal lines meet—is further to the right, indicating that more programs can take full advantage of the processor's computational power.

In a comparison between the NEC SX-9 vector processor and the Intel Core i7, we see that the SX-9 has a much higher memory bandwidth, pushing its ridge point far to the right. This means that for many workloads, the SX-9 can achieve its peak computational performance, whereas the Core i7 may be limited by memory bottlenecks.

SIMD has proven to be a powerful tool for enhancing multimedia processing, from early MMX extensions to the modern AVX instructions we see today. Its ability to operate on multiple small data elements simultaneously makes it perfect for tasks like graphics, audio, and video processing, where performance matters most.

While SIMD lacks some of the flexibility of true vector processors, its ease of implementation and compatibility with existing CPU designs have made it a popular choice. With each new generation of SIMD instructions, we get closer to bridging the gap between specialized vector hardware and general-purpose CPUs, giving developers the tools they need to write efficient, high-performance code.

GPUs

For anyone diving into the world of high-performance computing, GPUs (Graphics Processing Units) are often at the forefront of the conversation. Not only do they excel at rendering graphics, but their powerful parallel processing capabilities make them a fantastic tool for scientific computations. With the rise of CUDA and similar frameworks, programming GPUs has become more accessible, making it possible for developers to leverage GPU power for more general-purpose computations.

In this blog post, we will explore the internal structure of NVIDIA GPUs, their terminology, and how their unique architecture helps solve complex data-parallel problems effectively. We'll take a deep dive into CUDA, NVIDIA's parallel computing platform, and unravel how its terminology and GPU hardware architecture work together to harness the incredible power of parallelism.

GPUs and the Evolution to General-Purpose Computing

For a few hundred dollars, anyone can purchase a GPU packed with hundreds (or even thousands) of parallel floating-point units, enabling impressive performance gains. Originally designed as graphics accelerators to enhance visuals in games and graphical applications, GPUs have evolved far beyond this purpose. They are now powerful tools for general-purpose computing—also known as GPGPU (General-Purpose computing on Graphics Processing Units).

The primary design focus of GPUs was to improve the performance of graphics-related calculations. However, the computing community quickly realized that the massively parallel architecture used for graphics could also be used to solve other problems. Thus, frameworks like CUDA emerged, enabling developers to program GPUs for a wide variety of tasks beyond just graphics. This paradigm shift opened the door for GPUs to be used in areas like machine learning, scientific simulations, and large-scale data processing.

Programming the GPU with CUDA

CUDA (Compute Unified Device Architecture) is NVIDIA's parallel computing platform that allows developers to harness the full power of GPUs. CUDA provides a C/C++-like programming environment, designed to make GPU programming approachable for developers who are already comfortable with these languages. It introduces a model where developers can write functions that run on either the CPU (host) or GPU (device), enabling fine-grained control over parallel computations.

One of CUDA's core concepts is the "CUDA Thread," which is the smallest level of parallelism. By allowing thousands of CUDA Threads to run concurrently, developers can tap into the various forms of parallelism available in GPUs—including multithreading, MIMD (Multiple Instruction, Multiple Data), SIMD (Single Instruction, Multiple Data), and even instruction-level parallelism. These threads are organized in a manner that enables efficient execution, all managed by the GPU itself, taking much of the burden off developers to manually handle parallel scheduling.

In CUDA, the function that runs on the GPU is marked with either __device__ or __global__, distinguishing between functions that are local to the device and those callable from the host (CPU), respectively. Variables that are to reside in GPU memory are also marked with similar qualifiers. This model allows developers to write specialized functions for the GPU that can execute in parallel across thousands of threads.

For example, consider a simple DAXPY operation (a common linear algebra computation). In the conventional C version, this loop runs sequentially:

void daxpy(int n, double a, double *x, double *y) {
    for (int i = 0; i < n; ++i) {
        y[i] = a * x[i] + y[i];
    }
}

In CUDA, this can be parallelized by splitting the workload across many threads, each handling one iteration of the loop:

__global__ void daxpy(int n, double a, double *x, double *y) {
    int i = blockIdx.x * blockDim.x + threadIdx.x;
    if (i < n) y[i] = a * x[i] + y[i];
}

The function is invoked by specifying how many threads and blocks are needed to handle the task:

int nblocks = (n + 255) / 256;
daxpy<<<nblocks, 256>>>(n, 2.0, x, y);

CUDA uses a grid-block-thread hierarchy, where threads are grouped into blocks, and blocks are grouped into grids. Each thread is responsible for a small portion of the overall computation, allowing the workload to be distributed and processed in parallel.

NVIDIA GPU Computational Structures

NVIDIA GPUs feature an architectural style that's markedly different from CPUs, and even from earlier vector processors. The GPU architecture includes several unique terminologies, such as Thread Block, SIMD Processor, Thread Scheduler, and Grid, which collectively orchestrate the execution of parallel tasks.

Thread Blocks: A Thread Block is a group of CUDA Threads that execute the same function concurrently on a GPU. These threads share resources like shared memory, and each Thread Block is assigned to a processor, called a multithreaded SIMD Processor.
Thread Block Scheduler: The Thread Block Scheduler is responsible for distributing Thread Blocks to the available SIMD Processors. Depending on the size of the workload, it assigns as many blocks as possible to ensure full utilization of all available hardware.
SIMD Thread Scheduler: Within each SIMD Processor, there is also a SIMD Thread Scheduler, which coordinates the execution of SIMD threads. Each SIMD thread executes a set of SIMD instructions, with each instruction computing across multiple SIMD Lanes in parallel. This scheduler utilizes a scoreboard to track ready-to-run threads and ensures efficient execution by picking the next available thread as soon as others stall.
Grids: A Grid is the collection of Thread Blocks that executes a particular CUDA kernel. In GPU computing, grids provide an abstraction that represents a complete computation, similar to how a vectorized loop represents computation in vector processors.

These architectural components allow the GPU to take advantage of deep parallelism, enabling it to execute many threads concurrently. The goal is to hide latency and keep the GPU fully utilized, which is particularly important because GPU performance depends on overlapping multiple operations efficiently.

The Challenge of Maximizing GPU Performance

Programming a GPU isn’t just about getting the code running on the hardware; it's about keeping it running efficiently. GPUs are designed with an architecture that thrives on massive parallelism, meaning they require a constant stream of independent operations to perform at their best. In CUDA, this means keeping Thread Blocks independent, enabling them to be scheduled in any order, and ensuring data locality to reduce memory latency.

To fully utilize a GPU, performance programmers need to consider the unique architecture: groups of 32 threads, called a Warp, are executed in lockstep. Misaligned memory access patterns and dependencies between threads can lead to inefficient execution. This is why performance optimization on GPUs often involves organizing the computation to maximize coalesced memory access and using shared memory to avoid costly accesses to global memory.

As the GPU continues to evolve, the architectural design of NVIDIA GPUs aims to achieve scalability across many models, from consumer-grade graphics cards to powerful data-center GPUs. Each generation brings improvements that help bridge the gap between general-purpose computing and specialized graphics processing.

The Fermi architecture, for example, introduced a number of changes, such as enhanced double-precision floating-point performance, the inclusion of an L2 cache, and more registers per Thread Block, which help GPUs perform not only traditional graphics tasks but also high-performance scientific computations.

NVIDIA Instruction Set, Branching, and Memory Hierarchies

The NVIDIA GPU architecture is a marvel of parallel computing, tailored for high-throughput tasks. Unlike traditional CPUs, which are designed for general-purpose sequential tasks, GPUs are highly specialized processors optimized to handle multiple operations simultaneously, making them ideal for graphics rendering and large-scale scientific computations. This blog dives into the intricacies of NVIDIA's GPU instruction set, branching mechanisms, and memory hierarchy—key components that enable the incredible performance seen in modern GPUs.

PTX: The Intermediate Instruction Set

NVIDIA GPUs rely on an intermediate instruction set called PTX (Parallel Thread Execution). PTX acts as an abstraction layer, hiding the specifics of the hardware instruction set while maintaining compatibility across GPU generations. Essentially, PTX instructions describe operations at the CUDA thread level and are later translated into hardware-specific instructions.

PTX uses virtual registers, allowing the compiler to optimize how many physical vector registers are assigned to each SIMD thread. This flexibility also aids in resource allocation, such as eliminating dead code and managing branch divergence more effectively.

A PTX instruction is typically represented in the following format:

opcode.type d, a, b, c;

Here, d represents the destination operand, while a, b, and c are source operands. The .type specifier indicates the data type, which could range from untyped bits to signed and unsigned integers or even floating-point numbers of varying bit widths (e.g., .b16, .u32, .f64). PTX thus allows for a fine-grained definition of operations suitable for GPU workloads.

Conditional Branching in GPUs: Handling Divergence

Conditional branching in GPU programming can be challenging. Unlike vector architectures that often implement branches in software, GPUs use specialized branch synchronization stacks and predicate registers to handle divergent execution paths. A branch diverges when different threads in the same warp follow different code paths, requiring GPUs to execute both paths sequentially, thus reducing efficiency.

In PTX, branches are managed using predicate registers that control whether each SIMD lane will execute a given instruction. When the branch diverges, a branch synchronization marker is used to push the current active mask onto the stack, ensuring that all possible execution paths are tracked effectively.

In scenarios where all lanes agree on the branch condition—either all true or all false—the PTX assembler optimizes by skipping the redundant instructions, thereby improving execution efficiency. However, when branching conditions are not uniform, execution must diverge, and the performance impact can be significant, reducing the efficiency by half for basic IF-THEN-ELSE statements.

NVIDIA GPU Memory Structures

NVIDIA GPUs utilize a sophisticated memory hierarchy to hide latency and maximize throughput. Each SIMD Lane has its own private section of off-chip DRAM called Private Memory. This memory holds the stack frame, registers that cannot fit in on-chip memory, and other private variables. Since these private memories are cached in L1 and L2, they facilitate quick access while reducing latency during function calls and register spilling.

Moreover, NVIDIA GPUs leverage Local Memory, an on-chip memory that is shared among SIMD Lanes within a Multithreaded SIMD Processor. However, this memory is only accessible by threads within the same block, effectively isolating access and reducing the complexity of synchronization. Local Memory is dynamically allocated when a thread block is created and freed upon its exit, ensuring efficient usage of limited on-chip resources.

Finally, GPU Memory refers to the off-chip DRAM shared across all thread blocks and processors. This global memory is slower compared to on-chip alternatives but can hold the large datasets often required by GPU applications. Efficient access to GPU Memory is a critical factor in GPU programming, as memory bottlenecks can easily negate the advantages offered by massive parallelism. To alleviate this, memory coalescing is used to group individual memory requests into larger, more efficient block requests when the addresses fall within the same memory block.

Optimizations and Challenges

The GPU's reliance on multithreading to hide DRAM latency is a defining feature of its architecture. Rather than employing large caches like a CPU, GPUs are designed to switch between threads during long memory access times, effectively utilizing their many cores. Local memory for stack frames and function calls is cached to ensure function execution is as efficient as possible, while PTX data transfer instructions work to coalesce memory requests and reduce overhead.

For developers, these features mean that programming for GPUs requires careful attention to memory locality and thread synchronization. Effective GPU programming is about minimizing divergent execution and optimizing memory accesses—key aspects that NVIDIA's architecture tries to mitigate through hardware-level innovations like branch synchronization stacks and shared memory caches.

Innovations in the Fermi GPU Architecture

The Fermi GPU architecture marked a significant leap forward in the evolution of NVIDIA GPUs, incorporating numerous innovations that enhanced performance, reliability, and compatibility. The multithreaded SIMD Processor of Fermi is more complex than the simplified version previously discussed. To improve hardware utilization, each SIMD Processor in Fermi features two SIMD Thread Schedulers and two instruction dispatch units. These schedulers can select two threads of SIMD instructions and issue one instruction from each to two sets of 16 SIMD Lanes, 16 load/store units, or 4 special function units. This means two independent threads of SIMD instructions can be scheduled every two clock cycles, enabling more efficient execution without the need to check for data dependencies in the instruction stream. This innovation is akin to a multithreaded vector processor capable of issuing vector instructions from two independent threads.

The Fermi architecture introduced several key innovations that brought GPUs closer to mainstream system processors compared to its predecessor, Tesla, and earlier GPU architectures:

Error Correcting Codes (ECC): To make GPUs reliable for long-running applications in data centers, Fermi included support for ECC to detect and correct errors in memory and registers. This feature, commonly used in traditional datacenters, ensures dependable operations across thousands of servers.
Faster Context Switching: Given the extensive state of a multithreaded SIMD Processor, Fermi included hardware support to enable faster context switching. Fermi GPUs can switch contexts in under 25 microseconds, roughly ten times faster than previous generations.
Enhanced Double-Precision Floating-Point Arithmetic: Fermi brought its double-precision floating-point arithmetic performance closer to that of conventional CPUs, achieving roughly half the speed of single-precision operations. This represented a significant improvement over the Tesla generation, where double-precision performance was just one-tenth of single precision. The peak double-precision performance of Fermi increased to 515 GFLOP/sec when using multiply-add instructions, compared to 78 GFLOP/sec in the prior generation.
Introduction of Caches for GPU Memory: Traditionally, GPUs relied on having enough threads to hide DRAM latency. However, variables like local data need to be shared across threads, and this motivated the inclusion of both L1 Data and L1 Instruction caches for each multithreaded SIMD Processor in Fermi. In addition, Fermi includes a unified 768 KB L2 cache shared by all SIMD Processors. This caching mechanism not only reduced bandwidth pressure on off-chip GPU Memory but also saved energy by minimizing the need for frequent off-chip DRAM access. Interestingly, the GTX 480 model has an inverted memory hierarchy, with an aggregate register file size of 2 MB, a combined L1 cache size between 0.25 and 0.75 MB (depending on the configuration), and a 0.75 MB L2 cache. The impact of this unusual memory hierarchy on real-world GPU applications was a subject of much interest.
64-Bit Addressing and Unified Address Space: Fermi introduced 64-bit addressing along with a unified address space for all GPU memories. This made it significantly easier to manage pointers in languages like C and C++, streamlining the development process.
Improved Atomic Instructions: The Tesla architecture was the first to include support for atomic instructions, but Fermi greatly improved their performance. Atomic operations became up to 20 times faster, taking just a few microseconds to execute. The handling of atomic instructions was assigned to a dedicated hardware unit associated with the L2 cache, outside of the multithreaded SIMD Processors, resulting in substantial performance improvements.

These innovations positioned the Fermi architecture as a major step towards bridging the gap between traditional CPUs and GPUs. With enhanced features like error correction, faster context switching, robust double-precision arithmetic, the introduction of L1 and L2 caches, 64-bit addressing, and accelerated atomic operations, Fermi pushed GPUs beyond their original niche roles in graphics and brought them much closer to general-purpose computation, especially for high-performance computing applications.

Similarities and Differences between Vector Architectures and GPUs

Vector architectures and GPUs share a surprising number of similarities, and their comparison can help demystify the often misunderstood realm of GPU architecture. Both architectures are designed for executing data-level parallel (DLP) programs, but they take different approaches to reach similar ends. This comparison will help deepen our understanding of what is needed for effective DLP hardware.

At their core, both vector architectures and GPUs are designed to process large volumes of data in parallel. GPUs use SIMD (Single Instruction, Multiple Data) processors that act similarly to vector processors. In fact, the multiple SIMD processors within a GPU can be viewed as independent MIMD (Multiple Instruction, Multiple Data) cores, similar to how vector computers have multiple vector processors. This perspective makes the NVIDIA GTX 480, for instance, appear like a 15-core system, with each core having 16 lanes capable of handling multithreading.

One fundamental distinction between vector processors and GPUs is the concept of multithreading. Multithreading is at the heart of GPU architecture, enabling the system to handle a massive number of threads and thus hide memory latencies. Conversely, traditional vector processors typically lack multithreading capabilities. This divergence is a crucial factor in how GPUs and vector architectures execute parallel tasks.

The differences are also evident in the handling of registers. In vector architectures like VMIPS, registers are designed to hold entire vectors, such as a contiguous block of 64 doubles. A single GPU vector, however, is distributed across the registers of all SIMD lanes, with the GPU thread managing up to 64 registers per SIMD thread, each containing 32 elements. This allows a total of 2048 elements, which is more than the 512 elements of a VMIPS vector processor, highlighting the support GPUs have for multithreading.

Both architectures use SIMD lanes that work in parallel, though GPUs have more lanes, resulting in shorter "chimes." A vector processor may have a vector length of 32, requiring multiple clock cycles to complete operations, whereas a GPU with a SIMD thread size of 32 elements can complete operations in as few as two or four clock cycles.

Another similarity is in the type of instructions executed. A PTX instruction in a GPU is equivalent to a vector instruction in vector processors, with a SIMD thread broadcasting the PTX instruction to all SIMD lanes. Both architectures also implement gather and scatter instructions, which refer to how data is loaded and stored. While vector architectures have explicit unit-stride load/store instructions, GPUs rely on the Address Coalescing Unit to ensure high memory bandwidth when threads access addresses that are spatially close.

Memory latency is another key point of divergence. Vector architectures amortize latency across an entire vector by pipelining the access—paying the latency once and transferring data for all vector elements. GPUs, in contrast, use multithreading to hide latency, continuously switching between threads to keep the processing units busy. Some researchers are even exploring how to add multithreading to vector architectures to combine the advantages of both systems.

The management of conditional branches is another area of similarity and difference. Both vector architectures and GPUs use mask registers to implement conditional branches, ensuring that all possible paths are taken even if only some elements are affected. However, in vector architectures, the compiler explicitly manages these mask registers, while in GPUs, the management is handled by hardware via branch synchronization markers and an internal stack.

While GPUs lack a control processor found in vector computers, they instead use a Thread Block Scheduler to assign tasks. The control processor in vector computers plays an important role in broadcasting operations, incrementing memory addresses, and handling unit and non-unit stride operations, which are all implicit in GPUs. The closest analogy in GPUs is the Thread Block Scheduler, but it requires more power and is less efficient compared to a vector control processor.

Finally, when it comes to handling scalar tasks, vector processors use a scalar processor to execute operations that would be inefficient in vector units. In GPUs, such operations would typically be managed by the system processor, but due to the overhead of communicating over a PCIe bus, it may instead be faster to disable all but one SIMD lane and execute the scalar task within the GPU itself. However, this GPU approach is less efficient and consumes more power than the scalar processor of a vector computer.

Similarities and Differences between Multimedia SIMD Computers and GPUs

At a high level, GPUs and multicore computers with Multimedia SIMD instruction extensions share several similarities. Both systems are multiprocessors, each featuring multiple SIMD lanes that allow for parallel processing. However, GPUs tend to have more processors and significantly more SIMD lanes, as well as far more extensive hardware support for multithreading. Innovations in GPUs have also resulted in improved performance for double-precision floating-point arithmetic, narrowing the gap with conventional CPUs.

Despite these commonalities, the two architectures diverge significantly in several ways. GPUs use smaller streaming caches optimized for bandwidth, while multicore processors use large multilevel caches designed to store entire working sets. Both systems employ 64-bit address spaces, but the physical memory available to GPUs is generally smaller compared to traditional multicore computers. Additionally, while both architectures support memory protection at the page level, GPUs do not implement demand paging.

The architectural differences go beyond numerical disparities in processors, SIMD lanes, and cache sizes. Multimedia SIMD instructions are tightly integrated with scalar processors in traditional computers, while in GPUs, they are separated by an I/O bus and often have separate memory systems. The caches in traditional multicore systems are also coherent, unlike in GPUs, where the multiple SIMD processors operate within a single address space but lack coherence between caches.

Another notable distinction is that GPUs support gather-scatter memory accesses, which are absent in multimedia SIMD instructions. This ability to coalesce and scatter memory addresses helps GPUs achieve high memory bandwidth in parallel applications, which is a significant advantage over traditional multicore systems that rely on multimedia SIMD.

In summary, while GPUs and both vector and multimedia SIMD architectures have considerable similarities, the differences—particularly around multithreading, memory access, and architectural integration—highlight the unique approaches each takes to achieve efficient data-level parallelism. As the boundaries between these architectures continue to blur with ongoing innovations, it will be fascinating to see how they evolve and influence each other in the quest for faster, more efficient parallel computing.

Detecting and Enhancing Loop-Level Parallelism

Loops are a treasure trove of potential parallelism in programs, driving both data-level parallelism (DLP) and thread-level parallelism (TLP). Understanding and exploiting loop-level parallelism allows us to harness the power of modern GPUs and vector architectures effectively. This section explores how compilers detect this kind of parallelism and how hardware can support these efforts.

To determine if a loop is parallel (or vectorizable), compilers look at data dependencies within loops. If data dependencies exist across iterations—known as loop-carried dependencies—the loop may not be parallel. However, if dependencies exist only within individual iterations, then the loop can be parallelized. Consider the following loop:

for (i = 999; i >= 0; i = i - 1)
  x[i] = x[i] + s;

In this example, each iteration is independent of the others. Thus, no loop-carried dependency exists, making this loop parallelizable. This is the kind of analysis that compilers do to uncover opportunities for parallel execution.

However, dependence detection is not always straightforward. When dealing with arrays, pointers, or pass-by-reference parameters, determining whether two references are dependent can become complex. To address this challenge, many compilers use methods like the greatest common divisor (GCD) test for simple affine array indices. This allows them to determine whether dependencies exist for basic loops. For example, if a loop index is expressed as a * i + b, the GCD test can help determine if there's a dependency between iterations, and thus, whether parallel execution is possible.

Finding and eliminating loop-carried dependencies is critical, not only for exploiting DLP in vector or GPU architectures but also for taking advantage of instruction-level parallelism (ILP), as seen in Very Long Instruction Word (VLIW) architectures. This process involves analyzing loop-level parallelism at a high level, often at or near the source level, instead of working with the machine code that emerges from the compiler.

One way to handle dependencies is to eliminate dependent computations through transformations. For instance, the following loop, which calculates a dot product, has a loop-carried dependency on the variable sum:

for (i = 9999; i >= 0; i = i - 1)
  sum = sum + x[i] * y[i];

This loop cannot be parallelized directly. However, by transforming sum into a vector (a process called scalar expansion), the loop becomes parallelizable:

for (i = 9999; i >= 0; i = i - 1)
  sum[i] = x[i] * y[i];

Now, each computation is independent, making it a parallel loop. Once the parallel operations are complete, a reduction step is needed to sum up all the values in sum:

for (i = 9999; i >= 0; i = i - 1)
  finalsum = finalsum + sum[i];

This reduction step is not parallel, but specific architectures, such as SIMD or vector architectures, have hardware features to perform such reductions efficiently. These features are also utilized in parallel computing environments like MapReduce, where reduction is a common parallelism operation.

Dependence analysis plays a key role in optimizing for vector, SIMD, and GPU architectures. It allows the compiler to uncover and transform opportunities for parallelism, thereby improving performance. However, such analysis has its limitations. It generally works well within single loop nests and when affine index functions are used. When code uses pointers or procedure calls, analysis becomes much harder, and in these cases, approaches like OpenMP or CUDA can be helpful in explicitly marking parallel loops.

Lastly, it's worth noting that parallelizing loops often requires taking into account the nuances of computer arithmetic. For instance, arithmetic operations may not be associative when performed with limited precision, which can lead to issues if transformations relying on associativity are applied blindly. Thus, such optimizations are usually left to the discretion of the programmer or need explicit compiler directives to be enabled.

Data-Level Parallelism