Generating Lever-Door Puzzles

A lever-door puzzle is a challenge where players navigate through a series of rooms by using levers connected to various doors. When a lever is activated, it toggles the state of one or more doors. The objective of the puzzle is to progress from the starting room to a final room that holds some sort of reward.

I came across this style of puzzle in the basement of “Draynor Manor” in the game Runescape. There might be a more general name for the type of puzzle, but as of this writing, I’m not aware of it.

Since I’m developing my own browser-based MMO, I wanted to create similar puzzles. I figured it would be a good way to grant optional rewards to players patient enough to solve the puzzles.

It can be generalized by building a graph where each room is a node, each door is an edge, and each room contains zero or more levers. Here is an example:

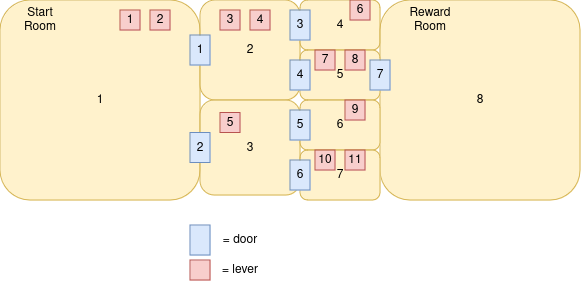
This layout is something that can be easily sketched together. The difficult part is determining which switches should toggle which doors in order to create a good puzzle.

This can be done manually, but it would be very difficult. For any given layout, the number of possible options is two to the power of the number of edges (because that is how many door combinations each lever could potentially toggle) to the power of the number of levers. For seven doors and eleven switches, there are 1.5111573e+23 possible puzzles!

So instead of doing it manually, I quickly realized I could write a script to generate these puzzles using a breadth-first search for each possible puzzle. I decided to use JavaScript because I can write it faster than any other language. With certain optimizations that I’ll talk about later, performance is good enough.

I begin by defining the graph itself in terms of nodes, edges, and switch locations.

var nodes = [1,2,3,4,5,6,7,8]
var edges = [[1,2], [1,3], [2,4],[2,5],[3,6],[3,7],[5,8]] // which rooms are connected by doors
var switches = [1, 1, 2, 2, 3, 4, 5, 5, 6, 7, 7] // which room each switch is in
var doorChanges = [];
for (var i = 0; i < Math.pow(2, edges.length); i++) {
    var binaryArray = Array.from(i.toString(2).padStart(edges.length, '0')).map(Number);
    // Optimization: make sure each lever opens 1 or 2 doors
    var numberOfOnes = binaryArray.reduce((count, bit) => count + bit, 0)
    if (numberOfOnes == 0 || numberOfOnes > 2) continue;
    doorChanges.push(binaryArray);
}
console.log('number of nodes: ', nodes.length)
console.log('number of edges: ', edges.length)
console.log('number of switches: ', switches.length)
console.log('possible changes: ', doorChanges.length)
var maxIndex = Math.pow(doorChanges.length, switches.length);
console.log('number of puzzles: ', maxIndex)

I calculate which doors each lever can potentially toggle by converting each number from 1 to 2^Edges to a binary string and then into an array. I remove options where there are more than two doors opened to simplify this puzzle a bit because there are already so many levers. Even with this simplification, there are still eight quadrillion potential trials.

Here is the general recursive algorithm for each trial:

1. Check if you are in a loop. If so, skip this trial and run the next attempt if it exists

2. Get every accessible node from your current location

   1. If you can access the final node, add the path you took to the success object

3. Get all available switches and add switching them to your list of attempts to try

4. Run the next attempt by recursively calling this function again

    function testScenario(currentLocation, currentEdges, visited, path, index, attempts) {
   
        // if you are in the same room, skip and try next attempt
        if (path.length >= 2 && path[path.length - 2] == path[path.length - 1]) {
            if (attempts.length > 0) {
                var attempt = attempts.shift();
                testScenario(attempt[0], attempt[1], attempt[2], attempt[3], attempt[4], attempts);
            }
            return;
        }
        currentEdges.sort(sortEdges);
        // if you're in the same situation as something previous, skip and try next attempt
        if (visited[currentLocation.toString() + '_' + currentEdges.toString()]) {
            if (attempts.length > 0) {
                var attempt = attempts.shift();
                testScenario(attempt[0], attempt[1], attempt[2], attempt[3], attempt[4], attempts);
            }
            return;
        }
        visited[currentLocation.toString() + '_' + currentEdges.toString()] = true;
   
        var allLocations = [];
        getAccessibleNodes(currentLocation, currentEdges, allLocations);
        for (var j = 0; j < allLocations.length; j++) {
            var location = allLocations[j];
   
            // check if the final location is accessible, if so add to success object
            if (location == nodes[nodes.length - 1]) {
                if (!successes[index] || successes[index].length > path.length) {
                    successes[index] = path
                }
                return;
            }
   
            // get all possible switches
            var availableSwitches = getAvailableSwitches(location);
            // try every permutation of available switches
            for (var i = 0; i < availableSwitches.length; i++) {
                var newEdges = flipSwitch(switchIndexes[availableSwitches[i]], currentEdges)
                var newPath = structuredClone(path);
                newPath.push(availableSwitches[i])
                attempts.push([location, newEdges, visited, newPath, index])
            }
        }
        // try next attempt
        if (attempts.length > 0) {
            var attempt = attempts.shift();
            testScenario(attempt[0], attempt[1], attempt[2], attempt[3], attempt[4], attempts);
        }
    }
   

This recursive function needs to be called for each trial. However if we did that for all 8 quadrillion, we would probably have to wait too long before finding a good solution. To speed things up, let’s just randomly choose a lever configuration and run as many trials as we can. This risks us losing out on the longest possible puzzle. However, there are probably millions of good solutions and we only need one. I set the number of trials so that I could generate puzzles for about an hour.

var startTime = Date.now();
var numTrials = 1e8;
for (var i = 1; i < numTrials; i += 1){
    var switchIndexes = [];
    var index = Math.floor(maxIndex * Math.random())
    var remaining = index
    for (var j = 0; j < switches.length; j++){
        switchIndexes[switches.length - 1 - j] = remaining % doorChanges.length
        remaining = Math.floor(remaining / doorChanges.length)
    }
    if (i % 1000000 == 0) {
        var elapsedTime = (Date.now() - startTime) / 1000;
        var totalTime = elapsedTime / (i / numTrials);
        console.log('index:', i,
            '\npercentComplete:', i / numTrials * 100,
            '\nhoursOfWork:', totalTime / 60 / 60)
        printLongest();
    }
    if (isDuplicateSwitch(switchIndexes)) continue;
    var currentEdges = [];
    var currentLocation = nodes[0]
    testScenario(currentLocation, currentEdges, {}, [], index, []);
}

At the end, I print out the longest “shortest“ path to the prize area for all configurations that were tested. I also print out which switches control which doors and the order to flip the switches in. I don’t necessarily need to choose the longest path one, but it would usually be the most interesting puzzle.

After an hour of running, I got a result which included 16 steps as the shortest path.

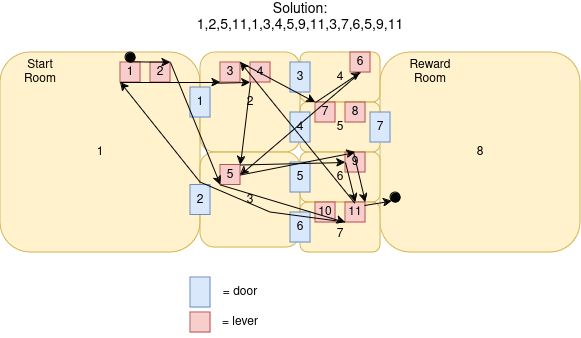
Here are which doors each lever toggles:

Now it’s time to open up blender and design the new area:

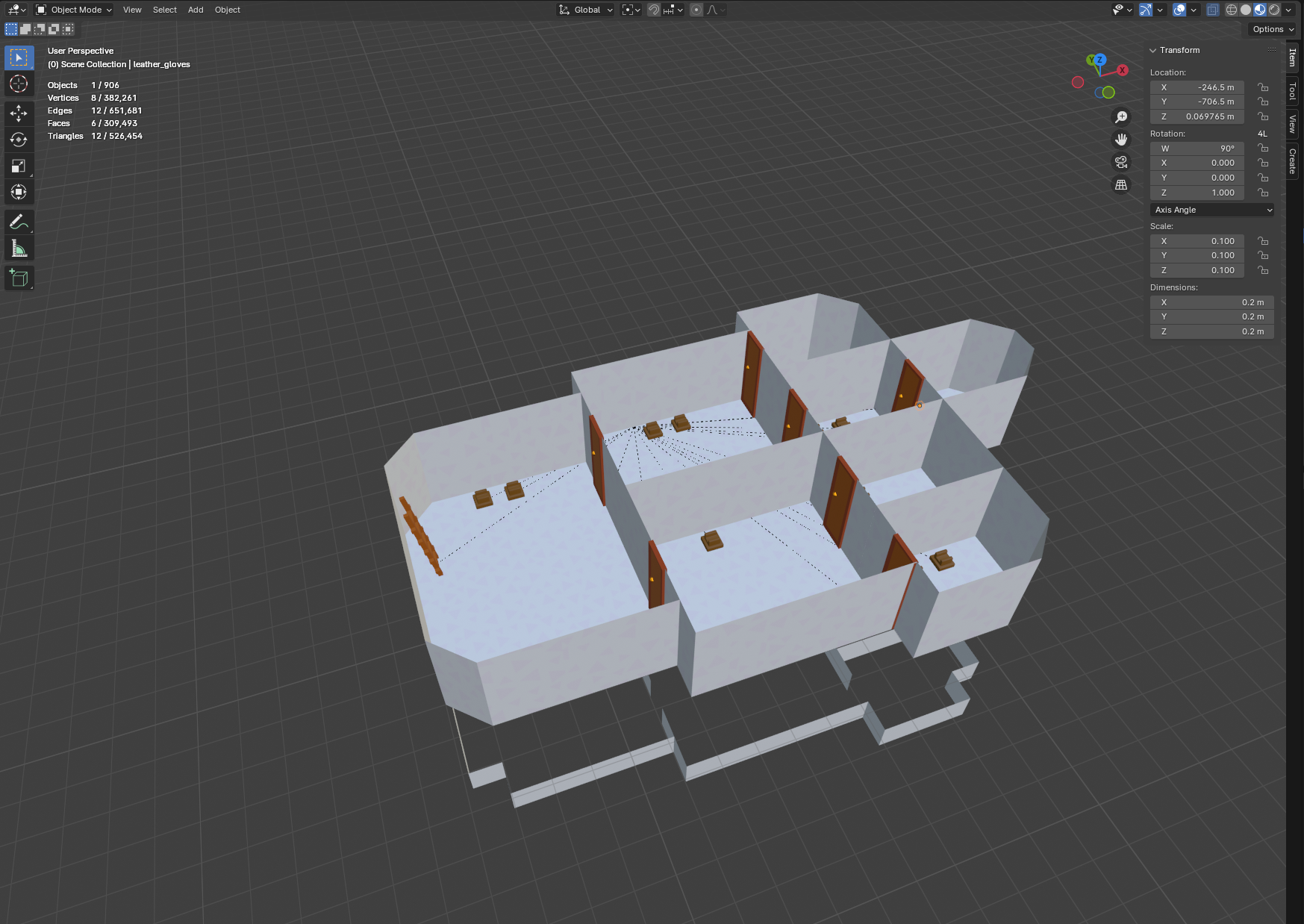
In my server code, I’ll associate the levers with the corresponding doors and let’s find out if it actually works:

Here is the full code on Github if you’d like to see the entire script and generate your own! This type of puzzle could possibly make a good standalone browser or mobile game.