Heap Sort Explained: A Simple and Detailed Overview

In our exploration of sorting algorithms, we've covered basic methods like Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, and Quick Sort. Each of these algorithms has its own strengths, from simplicity to handling large datasets efficiently. Now, let's explore Heap Sort, another efficient sorting algorithm that uses a special data structure called a heap to organize data.

Heap Sort is a comparison-based, in-place sorting algorithm with a consistent O(n log n) time complexity. This makes it particularly useful for large datasets where steady performance is important. Unlike the sorts mentioned earlier, Heap Sort builds a binary heap and uses its properties to efficiently locate and position the largest elements correctly.

Key concepts

1. Binary Heap:

   A binary heap is a complete binary tree that satisfies a specific order property. There are two types:

   • Max Heap: Every parent node is greater than or equal to its children. The largest element is found at the root.

   • Min Heap: Every parent node is less than or equal to its children, placing the smallest element at the root.

2. Heap Property:

   • The heap property is the rule that governs how elements are arranged in the binary heap. In a max heap, the heap property requires every parent node to be greater than or equal to its child nodes. This ensures that the largest element is always at the root.

3. Heapify Operation:

   • Heapify is the process of rearranging elements to maintain the heap property in a binary heap. When the heap property is violated, the heapify operation fixes the order by "bubbling" the element up or down until the property is restored.

   • For Heap Sort, we primarily use max-heapify to ensure that the largest element is always at the root.

Heap Sort Process

The Heap Sort process can use either a max heap or a min heap, depending on the desired sorting order:

1. Choose Heap Type Based on Sorting Order:

   • Max Heap for Ascending Order: If you want to sort the array in ascending order, build a max heap. This places the largest element at the root, allowing you to move it to the end of the array.

   • Min Heap for Descending Order: For sorting in descending order, build a min heap. This places the smallest element at the root, allowing you to move it to the end of the array for reverse sorting.

2. Build the Heap:

   • Start by transforming the array into the appropriate heap (either max or min, based on the desired order). This ensures that the root of the heap has either the largest or smallest element.

3. Sort the Array:

   • Step 1: Swap the root element with the last element in the heap. This places either the largest (in a max heap) or smallest (in a min heap) unsorted element in its correct final position.

• Step 2: Reduce the heap size by one, effectively removing the sorted element from the heap.

• Step 3: Apply the heapify operation to the root to restore the heap property.

• Step 4: Repeat these steps until all elements are sorted in the desired order.

Example

Suppose we have an array of unsorted integers: [3, 8, 5, 4, 1, 9, 2]

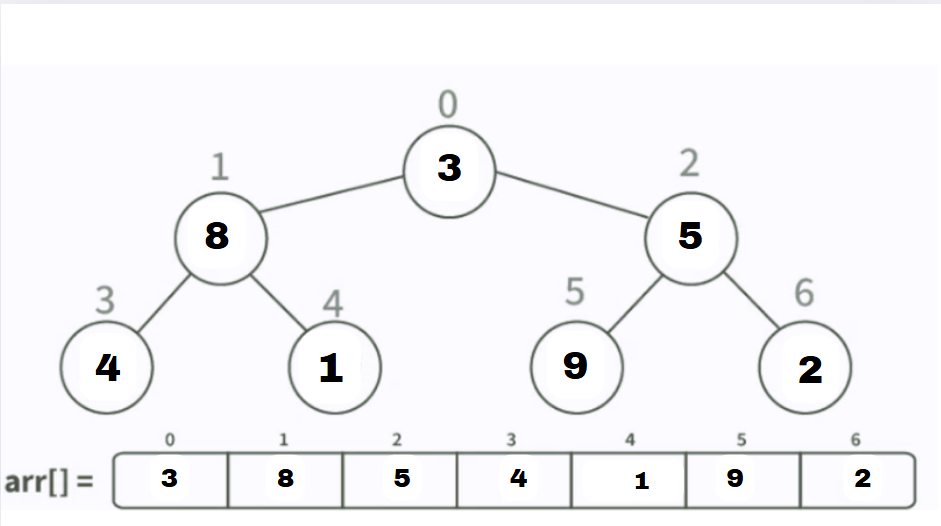
Step 1: Build a Max Heap

To sort in ascending order, we’ll build a max heap. This ensures the largest element is at the root of the heap. Here’s how we build the max heap from the array:

1. Initial Array: [3, 8, 5, 4, 1, 9, 2]

2. Start by heapifying from the last non-leaf node up to the root node to establish the max heap property.

3. Heapify Steps:

   Heapify Node at Index 2 (5):

   • Left Child = 9 (Index 5), Right Child = 2 (Index 6)

   • The largest value is 9 (left child), so we swap 5 and 9.

   • Array After Swap: [3, 8, 9, 4, 1, 5, 2]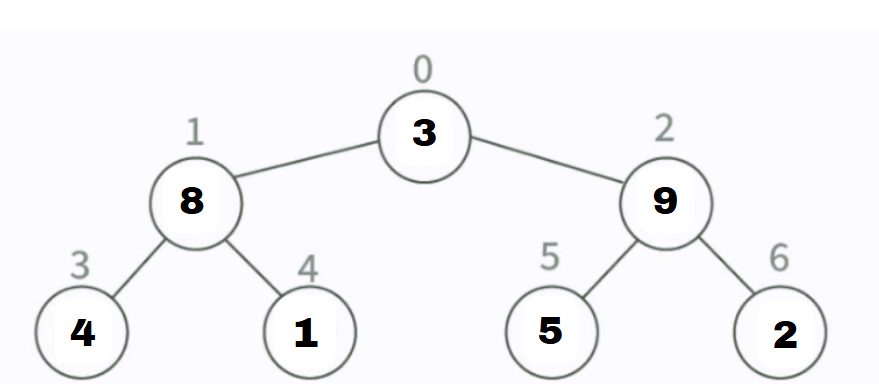

     

Heapify Node at Index 1 (8):

• Left Child = 4 (Index 3), Right Child = 1 (Index 4)

• 8 is already larger than both children, so no changes are needed.

Heapify Node at Index 0 (3):

• Left Child = 8 (Index 1), Right Child = 9 (Index 2)

• The largest value is 9 (right child), so we swap 3 and 9.

• Array After Swap: [9, 8, 3, 4, 1, 5, 2]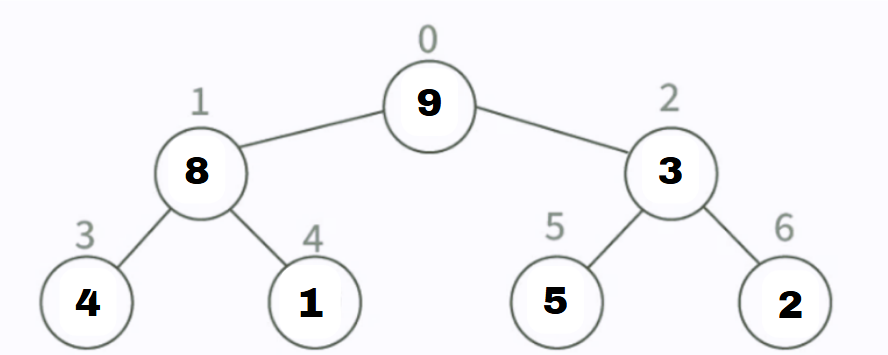

  

Max Heap Built: [9, 8, 5, 4, 1, 3, 2]

Step 2: Extract Elements and Sort

Now that we have a max heap, we’ll start sorting the array by moving the root (largest element) to the end of the array and reducing the heap size each time.

1. Extract 9 (Root) and swap it with the last element in the heap:

   • Array Before Swap: [9, 8, 5, 4, 1, 3, 2]

   • Swap 9 and 2: Array After Swap: [2, 8, 5, 4, 1, 3, 9]

   • Reduce heap size by one and heapify the root to restore the max heap property.

Heapify the Root (2):

• Left Child = 8, Right Child = 5

• Largest value is 8, so swap 2 and 8.

• Array After Heapify: [8, 2, 5, 4, 1, 3, 9]

• Heapify the new position of 2 (index 1):

  • Left Child = 4, Right Child = 1

  • Largest value is 4, so swap 2 and 4.

  • Array After Heapify: [8, 4, 5, 2, 1, 3, 9]

2. Extract 8:

   • Array Before Swap: [8, 4, 5, 2, 1, 3, 9]

   • Swap 8 and 3: Array After Swap: [3, 4, 5, 2, 1, 8, 9]

   • Heapify the root (3):

     • Left Child = 4, Right Child = 5

     • Largest value is 5, so swap 3 and 5.

     • Array After Heapify: [5, 4, 3, 2, 1, 8, 9]

3. Extract 5:

   • Array Before Swap: [5, 4, 3, 2, 1, 8, 9]

   • Swap 5 and 1: Array After Swap: [1, 4, 3, 2, 5, 8, 9]

   • Heapify the root (1):

     • Left Child = 4, Right Child = 3

     • Largest value is 4, so swap 1 and 4.

     • Array After Heapify: [4, 1, 3, 2, 5, 8, 9]

     • Heapify new position of 1:

       • Left Child = 2

       • Largest value is 2, so swap 1 and 2.

       • Array After Heapify: [4, 2, 3, 1, 5, 8, 9]

4. Extract 4:

   • Array Before Swap: [4, 2, 3, 1, 5, 8, 9]

   • Swap 4 and 1: Array After Swap: [1, 2, 3, 4, 5, 8, 9]

   • Heapify the root (1):

     • Left Child = 2, Right Child = 3

     • Largest value is 3, so swap 1 and 3.

     • Array After Heapify: [3, 2, 1, 4, 5, 8, 9]

5. Extract 3:

   • Array Before Swap: [3, 2, 1, 4, 5, 8, 9]

   • Swap 3 and 1: Array After Swap: [1, 2, 3, 4, 5, 8, 9]

6. Extract 2:

   • Array Before Swap: [1, 2, 3, 4, 5, 8, 9]

   • Swap 2 and 1: Array After Swap: [1, 2, 3, 4, 5, 8, 9]

After all extractions, the array is fully sorted:

Final Sorted Array: [1, 2, 3, 4, 5, 8, 9]

Pseudocode

Here’s a simple pseudocode for Heap Sort:

HEAP_SORT(arr):
    BUILD_MAX_HEAP(arr)
    for i from length(arr) - 1 down to 1:
        SWAP(arr[0], arr[i]) // Move current root to the end
        MAX_HEAPIFY(arr, 0, i) // Heapify root for reduced heap size

BUILD_MAX_HEAP(arr):
    for i from length(arr) // 2 down to 0:
        MAX_HEAPIFY(arr, i, length(arr))

MAX_HEAPIFY(arr, i, heap_size):
    left = 2 * i + 1
    right = 2 * i + 2
    largest = i
    if left < heap_size and arr[left] > arr[largest]:
        largest = left
    if right < heap_size and arr[right] > arr[largest]:
        largest = right
    if largest != i:
        SWAP(arr[i], arr[largest])
        MAX_HEAPIFY(arr, largest, heap_size)

Python code for heap sort

Let’s translate the above pseudocode into Python code:

def heap_sort(arr):
    def max_heapify(arr, i, heap_size):
        largest = i
        left = 2 * i + 1
        right = 2 * i + 2

        if left < heap_size and arr[left] > arr[largest]:
            largest = left
        if right < heap_size and arr[right] > arr[largest]:
            largest = right

        if largest != i:
            arr[i], arr[largest] = arr[largest], arr[i]
            max_heapify(arr, largest, heap_size)

    def build_max_heap(arr):
        for i in range(len(arr) // 2 - 1, -1, -1):
            max_heapify(arr, i, len(arr))

    build_max_heap(arr)

    for i in range(len(arr) - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]
        max_heapify(arr, 0, i)

# Test the heap sort
arr = [3, 8, 5, 4, 1, 9, 2]
heap_sort(arr)
print("Sorted array:", arr)

Advantages and Disadvantages

Advantages:

• Time Complexity: Heap Sort has a consistent time complexity of O(nlog⁡n)O(n \log n)O(nlogn), making it efficient for large datasets.

• In-Place: Unlike algorithms that require additional memory, Heap Sort operates in place without requiring extra space.

• Not Affected by Initial Order: The performance of Heap Sort remains the same whether the data is random, partially sorted, or reverse sorted.

Disadvantages:

• Not Stable: Heap Sort is not a stable sorting algorithm, which means it does not maintain the relative order of equal elements.

• Cache Performance: It may not be as cache-friendly as other algorithms like Quick Sort, as it frequently accesses non-contiguous memory locations.

Time complexity

• Best Case: The algorithm consistently performs O(n log n) regardless of input order.

• Average Case: O(n log n)– Heap Sort’s performance remains stable with random inputs.

• Worst Case: O(n log n) – Heap Sort doesn’t degrade like Quick Sort, staying O(n log n) even with the worst input arrangement.

Conclusion

And that brings us to the end of our discussion on sorting algorithms! We've explored various methods, including Bubble Sort, Selection Sort, Insertion Sort, Merge Sort, Quick Sort, and Heap Sort, showcasing different ways to organize data. Each algorithm has its features and strengths, making it important for anyone interested in Data Structures and Algorithms to understand them. If you're eager to learn more, other sorting algorithms like Radix Sort, Counting Sort, Bucket Sort, and Shell Sort are also worth exploring. Here are some links to those topics for further reading:

• Radix Sort: Efficient for sorting integers and works by processing individual digits.

• Counting Sort: Suitable for sorting a range of integers, leveraging a counting array.

• Bucket Sort: Distributes elements into buckets and sorts each bucket individually.

• Shell Sort: A generalization of Insertion Sort that allows the exchange of items far apart.

Thanks for following along, and happy coding! Keep exploring and having fun with it!