Ei... ECDSA? bora!?

Maicol KaiserMaicol Kaiser
9 min read

Table of contents

Ok, ok, este é meu primeiro artigo, então… pega leve comigo 🙏.

Neste ano de 2024, precisei lidar com algo muito incrível chamado ECDSA, e o melhor… eu não fazia ideia do que se tratava (não que eu domine completamente hoje, mas… já sei o suficiente para escrever este artigo), e… aposto que você também não, então bora comigo e vamos ver o poder dessa tecnologia 😜.

O que é ECDSA?

Bom, se a gente simplesmente partir para a definição de cada letrinha, significa (Elliptic Curve Digital Signature Algorithm), em bom portugues seria algo como → “Um monte de código que usa matematica pra assinar coisas".

De forma prática, o ECDSA permite que uma pessoa prove que é proprietaria de uma chave privada sem revelar a chave, assinando digitalmente um conteúdo que outras pessoas possam verificar usando a chave pública.

Este algoritmo se encaixa muito bem em:

  • Blockchain e Criptomoedas

  • Segurança de Redes

  • Assinaturas Digitais

Já ouviu falar em curva eliptica? pois então, eu até pouco tempo atrás também não, se segura que a gente vai dar uma longa volta… E… só pra reforçar… relaxa, se você conseguir chegar até o final, tenho certeza que você vai me agradecer.

O que é curva eliptica e porque eu preciso delas?

Curvas elípticas nos ajudam a definir uma espécie de caminho de mão única, onde é fácil realizar certas operações matemáticas, mas extremamente difícil revertê-las.

Em uma curva elíptica, é fácil multiplicar um ponto específico várias vezes para obter um novo ponto, mas é extremamente difícil descobrir quantas vezes a multiplicação foi feita para chegar naquele ponto resultante. Esse problema de encontrar o número de multiplicações necessárias é conhecido como o problema do logaritmo discreto e é o fundamento da segurança na criptografia de curvas elípticas(dá uma olhada nas referências depois).

Qual a aparência do monstro? 🤔

$$y 2 =x 3 +ax+b$$

Bora entender 🧐

Primeiramente a e b → são constantes que determinam a forma específica da curva (mais sobre formas de curva nas referências).

Cada combinação gera uma curva diferente e elas tem uma caracteristica interessante, onde os pontos da curva podem ser adicionados de forma unica para formar novos pontos. Usando o Desmos você consegue visualizar o que eu estou tentando dizer.

O X da equação, é relacionado a posição horizontal de um ponto na curva. Digamos que temos uma curva onde a = 2 e b = 3 então a equação ficaria

$$y 2 =x 3 +2x+3$$

Ok, mas… e se a gente escolher o valor do X? por exemplo… 1

$$y^2 = 1^ 3 + 2 . 1 +3$$

Podemos dizer que…

$$y 2 = 1 + 2 + 3 = 6$$

Doido né? chegamos no valor do Y definindo a forma da curva através das constantes A e B, e a posição de um ponto horizontal na curva através do x.

$$y^2 = ± \sqrt{6} ≈ ±2.449$$

Dai chegamos na conclusão que os pontos (1, 2.449) e (1, -2.449) são validos na curva.

Se a gente pegar um ponto inicial e for dando novos saltos, teremos algo semelhante a isto:

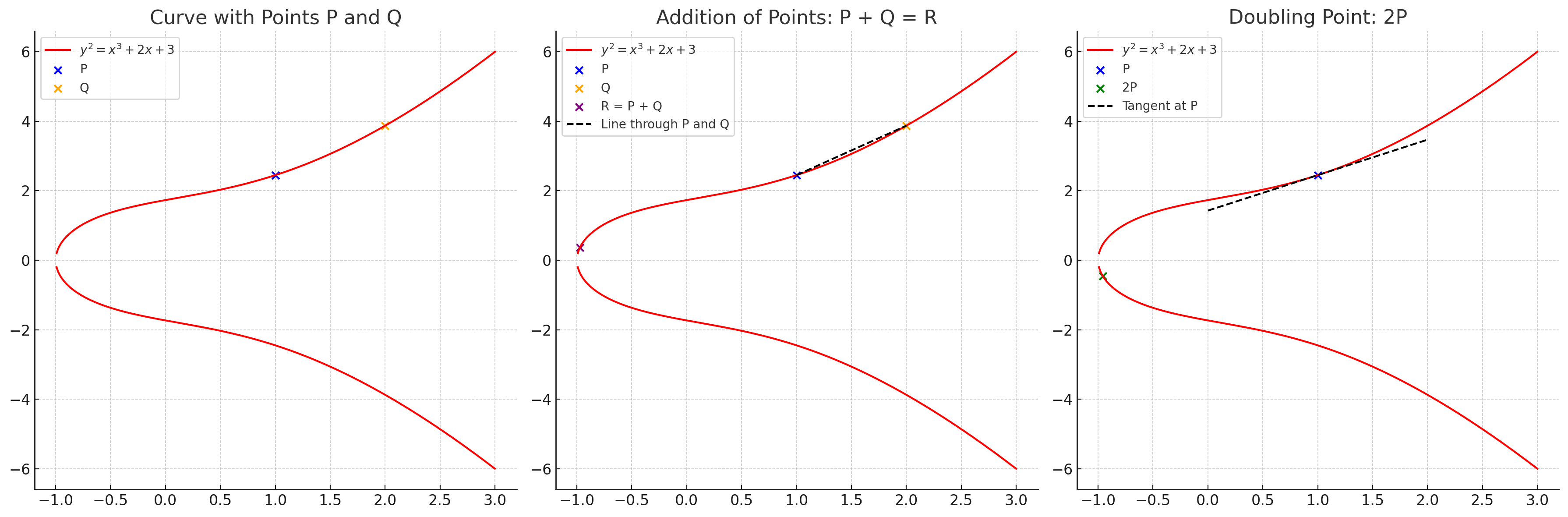
Primeiro gráfico:

  • a = 2 e b = 3

  • Os pontos P em azul e o Q em laranja

  • Estes são os pontos iniciais. Vamos usar eles nas proximas operações.

Segundo gráfico:

  • Usa o P e o Q gerado anteiormente

  • A soma dos pontos P + Q resulta no novo ponto, que chamamos de R

Terceiro gráfico:

  • Usamos a duplicação de pontos para que através da tangente que cruza a curva, acabamos chegando em outro ponto, chamado de 2P.

Espero que as ilustrações acima, tenham ajudado a entender como os pontos se relacionam. Acabamos usando a adição e duplicidade de pontos na curva.

Essas operações são a base de como o ECDSA funciona. No ECDSA, multiplicamos um ponto inicial na curva várias vezes para gerar uma chave pública segura, e a posição resultante no "caminho" da curva é usada como parte do processo de assinatura digital.

Cada ponto ( 𝑥 , 𝑦 ) na curva tem um papel específico. Ao multiplicar um ponto várias vezes, obtemos novos pontos, mas descobrir o número de multiplicações necessárias para chegar a um ponto específico é extremamente difícil — e essa dificuldade é o que torna o ECDSA seguro.

E eu sou responsável por definir estes valores?

Tá perdidinho né… eu também estava, relaxa que só piora, mas já adiantando, NÃO!

Existem alguns tipos de curvas padrão, como:

  • ecp256k1→ usado em blockchain

  • secp256r1 → usado nos protocolos TLS e SSL

  • secp384r1 → criptografar chaves públicas para segurança a longo prazo com alto nível de segurança, também TLS, SSL e SSH .

Estas curvas já tem seus valores previamente definidos. O pessoal do SECG (Standards for Efficient Cryptography Group) e NIST (National Institute of Standards and Technology) já cuidou disso pra gente, os valores, garantem segurança e compatibilidade, então apesar de saber que existe, não precisamos nos preocupar com isto 😜👌(nas referências temos mais detalhes)

Chega de Teoriaaaaaa 😣🤯

Sobreviveu? tá com pique? então vamo dale!

Gerando o par de chaves

Vamos utilizar o openssl que é uma ferramenta para geração de chaves. Esta chave gerada é compativel com ECDSA.

Lembra da curva secp256k1? é aqui que ela brilha ✨

Podemos gerar o par em conjunto

openssl ecparam -name secp256k1 -genkey -noout -out secp256k1_key.pem

E extrair o par de chaves publica e privada de uma única vez

openssl ec -in secp256k1_key.pem -noout -text

****** OUUUU *******

Podemos gerar apenas a chave privada

openssl ecparam -name secp256k1 -genkey -noout -out private_key.pem

Extraimos a chave pública baseado na chave privada gerada

openssl ec -in private_key.pem -pubout -out public_key.pem

Precisamos da chave pública em formato Hexadecimal não compactado para realizar as assinaturas, podemos gerar ela da chave publica ou diretamente da chave privada, abaixo vou deixar as duas abordagens.

### Extraindo da chave pública
openssl ec -pubin -in public_key.pem -outform DER -out public_key.der
tail -c 65 public_key.der | xxd -p -c 65

### Extraindo da chave privada
openssl ec -in private_key.pem -pubout -outform DER | tail -c 65 | xxd -p -c 65

A chave vai iniciar com 0x04 ou 04, que significa que não está compactada, e depois temos a sequencia de 32 bytes para cada uma das coordenadas x e y da chave pública em hexadecial total de 64 bytes.

### Chave completa
echo -e "### Chave completa\n""04eb59103e1bf87fc458f0cd188c51f1a872beae04\
e4df620d47e7282e8afee09fa5ef139bc781bfc42538f59dcc42e01e5d7e49f531d22e635\
0dfa70ea23cb040"

### Em partes

## 2 caracteres
04

## 64 caracteres
eb59103e1bf87fc458f0cd188c51f1a872beae04e4df620d47e7282e8afee09f

## 64 caracteres
a5ef139bc781bfc42538f59dcc42e01e5d7e49f531d22e6350dfa70ea23cb040

Devirando o endereço ethereum das chaves

Agora que conseguimos chegar na chave pública não compactada em formato hexa, conseguimos derivar desta chave um endereço ethereum, que basicamente define de forma pública uma referência de quem é o proprietário da chave.

Para isso vamos precisar de mais uma nome estranho, Keccak-256, esse rapaz é uma função de hash criptográfica que consegue gerar o hash que será utilizado para definir o endereço ethereum.

Existe uma receita definida pelos desenvolvedores do ethereum (olha as referências 😉)

# Hash inteiro
118a5195281508ca5ab70437c8496f9c8b1922627a4597bb9702b7ad7a9ac55c

O endereço é obtido a partir dos últimos 20 bytes do hash Keccak-256 da chave pública sem o prefixo 0x04.

# ultimos 20 bytes
c8496f9c8b1922627a4597bb9702b7ad7a9ac55c

Estes 20 bytes ou 160 bits que recuperamos, representam o endereço ethereum no formato hexadecimal e tem 40 caracteres. Ainda precisamos adicionar o prefixo 0x como uma ceraja no bolo 🍰.

### Endereço ethereum
0xc8496f9c8b1922627a4597bb9702b7ad7a9ac55c

Acha que acabou? peraí que tem mais uma ultima coisinha.

Foi introduzida uma etapa no processo para garantir que o endereço fique ainda mais seguro, usando um checksum, aplicando o keccak-256 ao endereço após ser convertido para maiúsculo baseado em algumas regras. Nas referências você vai encontrar o link para o EIP-55 Ethereum Improvement Proposal (EIP).

### Endereço final com o EIP-55 aplicado \0/
0xc8496F9C8B1922627A4597bb9702b7ad7A9AC55C

Abaixo disponibilizei alguns exemplos de código 😉

Javascript

https://codepen.io/vakaman/pen/yLmEGwv

Python

Para conseguir ver as rotas, onde eu mostro o funcionamento dos recursos, você vai precisar clicar no Ports e então localizar a porta 5000, depois só clicar no icone que diz Preview in editor e escolher a rota `Calculate Address` (talvez exista uma forma de fazer isso automaticamente, mas eu não achei como… então… me ajuda ai!)

https://codesandbox.io/s/ecdsa-python-3fydf3?embed=1&file=%2FREADME.md&showConsole=true

Assinando uma mensagem

Legal extrair o endereço ethereum né?… até então você deve tá pensando, onde esse maluco quer chegar com isso? E eu digo… calma, agora que a brincadeira fica interessante. Vamos usar a chave privada para realizar a assinatura de uma mensagem, se liga só!

No exemplo, vamos assinar a seguinte mensagem

    message = {
        "nome": "Maicol Oliveira",
        "idade": 34,
        "profissao": "Desenvolvedor"
    }

Consumindo a rota → sign_message, vamos ter o retorno da assinatura

{
  "assinatura": "b9092c7341aaac850c6209a800a0761d9333eb02e765461fd061137ee1bb259e0d90fe911ca5aa0e201e7d512d68d0dba97654d8dd0d0e9588449e9c659cc591"
}

Agora vamos validar esta assinatura, na rota → validate_signature_route, com a nossa chave privada, a mesma que usamos para assinar 😉

{
  "assinatura": "0x155f92d8c68a6741d4074b40d021bdc6e148aabb37ce43f8ce33d3720441c22d7405f748267537fa1ba683bc671e481d229f164a4f79e39bee5febade5861d9d",
  "is_valid": true,
  "message": {
    "idade": 34,
    "nome": "Maicol Oliveira",
    "profissao": "Desenvolvedor"
  }
}

BINGO!!! a assinatura é válida, incrível não é mesmo?

🧐🧐🧐🧐 Tá e… o que eu faço com isso?

Sei lá mano… te mostrei a ferramenta, boa sorte em onde você vai aplicar!🫠😂😅

Código de referência aqui

https://codesandbox.io/s/ecdsa-python-3fydf3?embed=1&file=%2FREADME.md&showConsole=true

Historinha para ajudar…

Tá.. blz, senta que lá vem a história, vamos fazer uma analogia, e depois… você que decide onde vai usar ok?

Imagine que você quer enviar uma mensagem secreta para seu amigo, mas precisa que alguém a transporte para você, e essa pessoa não pode descobrir o conteúdo e também não pode alterálo.

Como Proteger o Segredo? 🤔

Simples! coloque um “selo especial” 📩:

  • Você coloca sua mensagem em um envelope e usa este “selo especial” para fechá-lo. Esse selo é algo que só você sabe fazer – é único e impossível de replicar. O transportador pode ver o envelope, mas ele não consegue abrir sem estragar o selo.

  • Seu amigo conhece o selo. Assim, quando ele recebe o envelope e vê o selo intacto, ele sabe que:

    • A mensagem de fato veio de você

    • Ninguém abriu ou alterou o conteúdo no caminho

O Transportador Não Pode Interferir:

  • Quem transporta o envelope pode ver que ele tem seu selo, mas não tem como abrir e selar o envelope de novo da mesma forma.

Com isso entendemos que o suposto “selo especial” é a assinatura digital, o segreto que cria o selo é a sua chave privada, o amigo que verifica o selo é a chave pública, o conteúdo da mensagem ou o segredo que ela tem é o conteúdo, seja ele um texto ou um documento e o transportador é o canal de comunicação que pode ser a internet ou outro meio de transporte dessas informações.

Conclusão

Enfim… chegamos ao final, espero de coração que eu tenha ajudado. Tentei trazer de uma forma leve e mais didatica possível. Ficaria muito feliz com seu ponto de vista sobre o meu primeiro artigo e deixo completamente aberto o canal para feedback.

Referências

Ferramentas

0
Subscribe to my newsletter

Read articles from Maicol Kaiser directly inside your inbox. Subscribe to the newsletter, and don't miss out.

ECDSABlockchainkeccak256secp256k1

Written by

Maicol Kaiser
Maicol Kaiser

I am a systems architect with solid experience in developing scalable and high-performance solutions. My work primarily involves cloud technologies, advanced networking (BGP, OSPF, VRF), and relational and non-relational databases. I specialize in designing and implementing RESTful APIs, following best practices like SOLID, Clean Architecture, and DDD to ensure clean, maintainable code. My main stack includes PHP (Symfony), Java, Python, and JavaScript, as well as containerization tools like Docker and Kubernetes. I also work with distributed messaging queues (SQS, RabbitMQ, Kafka) for event-driven systems. I'm always focused on developing robust and reliable solutions, applying rigorous testing methodologies (TDD), and optimizing every aspect of the applications I build.