Elliptic curve trên trường số thực

Đường cong elliptic đóng vai trò cực kỳ quan trọng trong công nghệ mật mã hiện đại vì tính hiệu quả trong không gian lưu trữ và bảo mật vượt trội so với các công nghệ mã khóa công khai truyền thống như RSA. Hãy xem bảng so sánh bên dưới để thấy sự hiệu quả của mã hóa trên đường cong so với RSA:

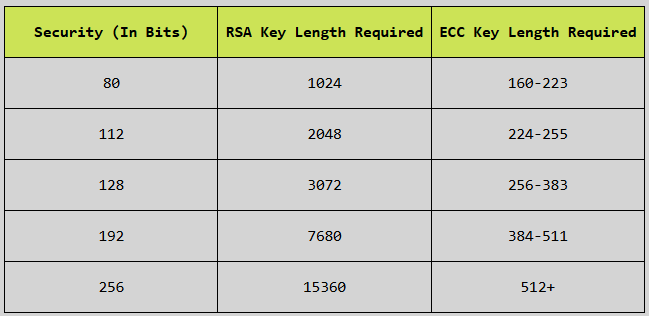
Ở bài viết này, mình muốn giới thiệu một số phép toán được định nghĩa trên đường cong trên trường số thực để bạn đọc dễ hình dung. Tuy nhiên, trong công nghệ mật mã, người ta sử dụng đường cong elliptic trên trường hữu hạn các số nguyên tố, mình sẽ giới thiệu ở bài viết sau.

Giới thiệu

Đường cong elliptic là cấu trúc đại số có dạng biểu diễn là:

$$y^2 = x^3 + ax^2 + bx + c$$

Với \(a, b\) là các hằng số. Về mặt đồ thị, đường cong có 2 dạng như bên dưới:

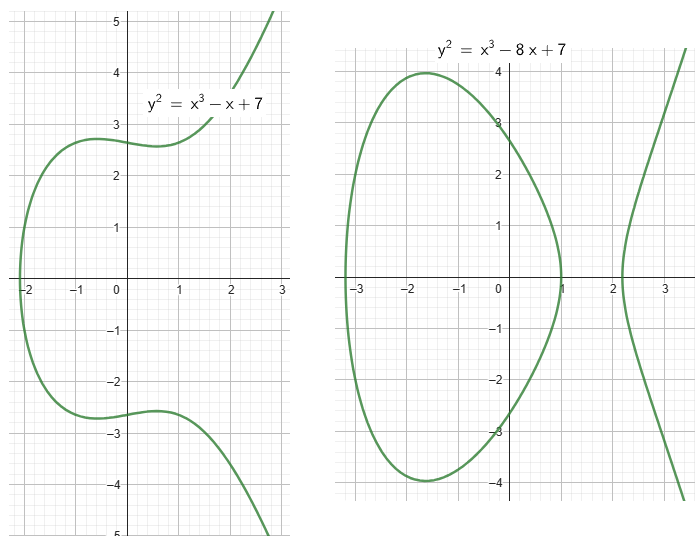
Các phép toán trên đường cong elliptic

1. Phép cộng hai điểm

   Gọi hai điểm \(A(x_A, y_A), B(x_B, y_B)\) là hai điểm trên đường cong \(E\). Ta định nghĩa phép cộng của 2 điểm này bằng cách:

   • Tìm giao điểm \(C(x_C, y_C)\) của đường thẳng \(AB\) và đường cong \(E\)

   • Lấy điểm \(D(x_D,y_D)\) đối xứng với \(C(x_C,y_C)\) qua trục hoành. Điểm \(D\) là kết quả của phép cộng: \(A+B\). Minh họa như hình dưới:

     

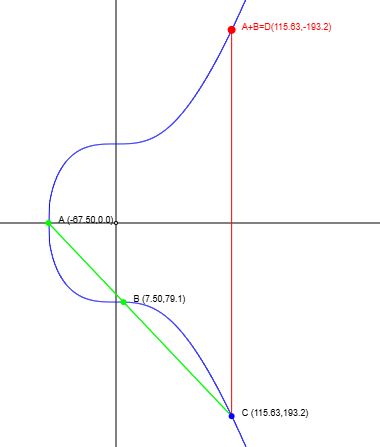
2. Phép nhân scalar với một điểm

   Hãy tưởng tượng rằng điểm \(A\) cố định, điểm \(B\) tịnh tiến dần đến điểm \(A\), gần đến nỗi \(B \) trùng với \(A\). Lúc này, đường thẳng \(AB\) biến thành tiếp tuyến tại \(A\) của đường cong \(E\), xác định điểm \(D\) như trên phép cộng, lúc này ta có thể nói: \(A+A = D = 2\times A\). Đây chính là cơ sở của phép nhân scalar 1 điểm trên đường cong với một số nguyên. Tương tự, ta có thể tính: \(3 \times A = A + 2 \times A; 4\times A = A + 3 \times A ; \dots\)

   Có một lưu ý rằng tồn tại một số điểm trên đường cong mà tại đó không tồn tại tiếp tuyến hoặc tiếp tuyết tại điểm đó không cắt đường cong. Ví dụ:

   

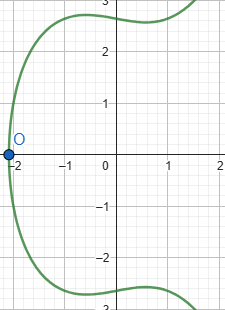
   Tiếp tuyến tại điểm \(O\) của đường cong song song với trục tung và không cắt đường cong tại điểm nào. Điểm \(O\) được gọi là điểm kỳ dị của đường cong, phép nhân scalar \(O \times n = O\).

Demo