Linear Regression
 Anix Lynch
Anix LynchLinear Regression Math
Suppose we have a small dataset of points showing the relationship between study hours ( \( x \) ) and test scores ( \( y \) ):
| Study Hours \( x \) | Test Score \( y \) |
| 1 | 2 |
| 2 | 3 |
| 3 | 5 |
We want to find the line of best fit to predict test scores based on study hours.
Step 1: Calculate Means
First, find the mean of \( x \) and \( y \) :
\( \bar{x} = \frac{1 + 2 + 3}{3} = 2 \)
\( \bar{y} = \frac{2 + 3 + 5}{3} = 3.33 \)
Step 2: Calculate the Slope ( \( m \) )
Using the formula for the slope \( m \) : \( m = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2} \)
Plugging in values:
Calculate \( (x_1 - \bar{x})(y_1 - \bar{y}) = (1 - 2)(2 - 3.33) = (-1)(-1.33) = 1.33 \)
Calculate \( (x_2 - \bar{x})(y_2 - \bar{y}) = (2 - 2)(3 - 3.33) = (0)(-0.33) = 0 \)
Calculate \( (x_3 - \bar{x})(y_3 - \bar{y}) = (3 - 2)(5 - 3.33) = (1)(1.67) = 1.67 \)
Sum of numerators: \( 1.33 + 0 + 1.67 = 3 \)
Now, calculate \( \sum (x_i - \bar{x})^2 \) :
\( (1 - 2)^2 = 1 \)
\( (2 - 2)^2 = 0 \)
\( (3 - 2)^2 = 1 \)
Sum of denominators: \( 1 + 0 + 1 = 2 \)
So, \( m = \frac{3}{2} = 1.5 \) .
Step 3: Calculate the Intercept ( \( b \) )
Using the formula for the intercept: \( b = \bar{y} - m \cdot \bar{x} \)
Substitute the values: \( b = 3.33 - (1.5 \cdot 2) = 3.33 - 3 = 0.33 \)
Step 4: Form the Regression Line
The best-fit line equation is: \( y = 1.5x + 0.33 \)
Step 5: Make Predictions
To predict the test score ( \( y \) ) for 4 hours of study ( \( x = 4 \) ): \( y = 1.5 \cdot 4 + 0.33 = 6 + 0.33 = 6.33 \)
Prediction: A student studying for 4 hours is predicted to score approximately 6.33.
10 Q&A
What is Linear Regression?
- Answer: Linear regression is a statistical method for modeling the relationship between a dependent variable and one or more independent variables by fitting a linear equation to observed data.
Explain the difference between simple and multiple linear regression.
- Answer: Simple linear regression involves one independent variable to predict a dependent variable, while multiple linear regression uses multiple independent variables.
What is the equation for a simple linear regression model, and what do each of the terms represent?
- Answer: The equation is \( y = mx + b \) , where \( y \) is the predicted value, \( x \) is the independent variable, \( m \) is the slope (change in \( y \) for each unit change in \( x \) ), and \( b \) is the intercept (value of \( y \) when \( x = 0 \) ).
How do you interpret the coefficients in a linear regression model?
- Answer: The slope coefficient indicates the average change in the dependent variable for each unit change in an independent variable, assuming other variables are constant. The intercept is the expected value of the dependent variable when all independent variables are zero.
What is the purpose of the cost function in linear regression, and which cost function is commonly used?
- Answer: The cost function measures how well the model fits the data. The most common cost function in linear regression is the Mean Squared Error (MSE), calculated as \( \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \) , where \( y_i \) is the actual value and \( \hat{y}_i \) is the predicted value.
How does linear regression handle multicollinearity, and why is it a problem?
- Answer: Multicollinearity occurs when independent variables are highly correlated, which can cause instability in coefficient estimates. It makes it difficult to determine the individual effect of each variable. Methods like removing correlated variables, using ridge or lasso regression, or calculating the Variance Inflation Factor (VIF) can help address it.
What is the difference between R-squared and Adjusted R-squared?
- Answer: R-squared indicates the proportion of variance in the dependent variable explained by the model. Adjusted R-squared accounts for the number of predictors and adjusts R-squared to penalize for adding irrelevant variables, which helps evaluate model complexity and prevent overfitting.
What is overfitting in linear regression, and how can you prevent it?
- Answer: Overfitting occurs when a model learns noise in the training data rather than general patterns, leading to poor performance on new data. Techniques to prevent it include using simpler models, applying regularization (e.g., ridge or lasso regression), or using cross-validation.
Explain the assumptions of linear regression.
Answer:
Linearity: The relationship between independent and dependent variables is linear.
Independence: Observations are independent of each other.
Homoscedasticity: Constant variance of errors across all levels of the independent variables.
Normality: Errors are normally distributed.
How can you evaluate the performance of a linear regression model?
- Answer: Common evaluation metrics for linear regression include Mean Squared Error (MSE), Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and R-squared. These metrics help assess how well the model predicts the dependent variable.
These questions cover a range of topics from basic definitions to more advanced concepts like assumptions and multicollinearity, providing a well-rounded preparation for linear regression interviews.
Numpy Code
Here’s Python code to perform linear regression using the same dataset, along with the calculation of the slope, intercept, and prediction for a new value of \( x \) .
import numpy as np
# Dataset
x = np.array([1, 2, 3]) # Study hours
y = np.array([2, 3, 5]) # Test scores
# Step 1: Calculate the means
x_mean = np.mean(x)
y_mean = np.mean(y)
# Step 2: Calculate the slope (m)
numerator = np.sum((x - x_mean) * (y - y_mean))
denominator = np.sum((x - x_mean) ** 2)
m = numerator / denominator
# Step 3: Calculate the intercept (b)
b = y_mean - m * x_mean
# Display the slope and intercept
print(f"Slope (m): {m}")
print(f"Intercept (b): {b}")
# Step 4: Define the linear regression function
def predict(x):
return m * x + b
# Step 5: Make a prediction for 4 hours of study
x_new = 4
y_pred = predict(x_new)
print(f"Predicted test score for {x_new} hours of study: {y_pred}")
Explanation of the Code
Dataset: We define study hours (
x) and test scores (y) as numpy arrays.Mean Calculation: Calculate the mean of
xandy.Slope Calculation (m): Using the formula, we compute the numerator and denominator for the slope.
Intercept Calculation (b): Calculate the intercept using the mean values of
xandy.Prediction Function: Define a function
predict(x)to calculate \( y \) based on the best-fit line.Make a Prediction: Use
predict(x_new)to predict the test score for 4 hours of study.
Expected Output
Slope (m): 1.5
Intercept (b): 0.3333333333333335
Predicted test score for 4 hours of study: 6.333333333333334
This code calculates the slope and intercept, and then uses them to make predictions for a new value of \( x \) . Let me know if you need further explanation or if there’s anything else!
Yes, we can definitely use a more advanced library to perform linear regression with minimal code! Scikit-Learn is a popular Python library that provides built-in functions for linear regression, which automates much of the process, including calculations for slope, intercept, and predictions.
Scikit-Learn Code
from sklearn.linear_model import LinearRegression
import numpy as np
# Dataset
x = np.array([1, 2, 3]).reshape(-1, 1) # Reshape x for sklearn compatibility (2D array)
y = np.array([2, 3, 5])
# Initialize the model
model = LinearRegression()
# Fit the model to the data
model.fit(x, y)
# Display the slope (coefficient) and intercept
print(f"Slope (m): {model.coef_[0]}")
print(f"Intercept (b): {model.intercept_}")
# Predict for a new value of x (e.g., 4 hours of study)
x_new = np.array([[4]])
y_pred = model.predict(x_new)
print(f"Predicted test score for {x_new[0][0]} hours of study: {y_pred[0]}")
Explanation of the Code
Data Preparation: Scikit-Learn requires
xto be in a 2D array format, so we reshape it using.reshape(-1, 1).Initialize the Model: We create an instance of
LinearRegression.Fit the Model: Using
model.fit(x, y), we train the model on the dataset.Retrieve Slope and Intercept:
model.coef_[0]gives the slope ( \( m \) ).model.intercept_provides the intercept ( \( b \) ).
Prediction: We make a prediction for 4 hours of study using
model.predict.
Expected Output
Slope (m): 1.5
Intercept (b): 0.3333333333333335
Predicted test score for 4 hours of study: 6.333333333333334
Benefits of Using Scikit-Learn
Simplicity: Scikit-Learn handles the math, letting you focus on model building and evaluation.
Extensibility: Scikit-Learn can be easily extended to more complex models and tasks.
Efficiency: It’s optimized for speed and performance, suitable for larger datasets.
Using Scikit-Learn is ideal for quickly setting up regression models, especially when working with more advanced or large-scale machine learning tasks. Let me know if you’d like to explore more on this!
Let’s apply AutoML on the linear regression example we've been working with, focusing on predicting test scores based on study hours. For simplicity and consistency with the math in previous examples, I’ll use TPOT (Tree-Based Pipeline Optimization Tool) and configure it to perform linear regression automatically.
Visualization
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
# Dataset
x = np.array([1, 2, 3]).reshape(-1, 1) # Study hours
y = np.array([2, 3, 5]) # Test scores
# Initialize and fit the model
model = LinearRegression()
model.fit(x, y)
# Predictions for plotting the regression line
x_range = np.linspace(1, 3, 100).reshape(-1, 1) # Range of study hours for smooth line
y_pred = model.predict(x_range)
# Plotting the data points and the regression line
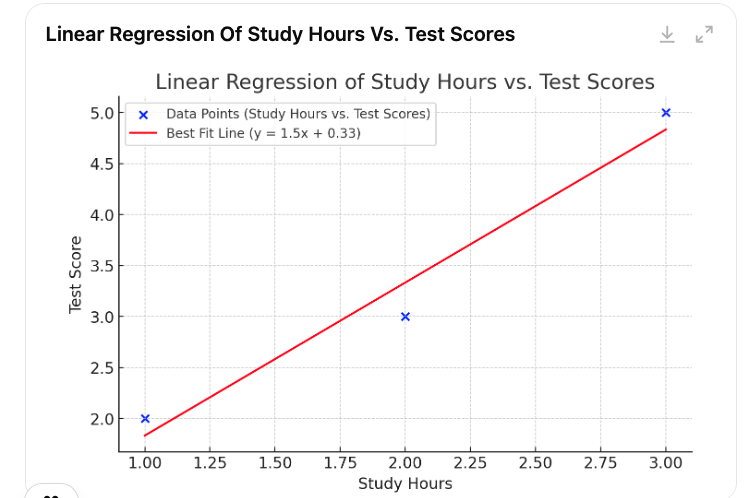
plt.figure(figsize=(8, 5))
plt.scatter(x, y, color='blue', label='Data Points (Study Hours vs. Test Scores)')
plt.plot(x_range, y_pred, color='red', label='Best Fit Line (y = 1.5x + 0.33)')
# Annotating the plot
plt.title("Linear Regression of Study Hours vs. Test Scores")
plt.xlabel("Study Hours")
plt.ylabel("Test Score")
plt.legend()
plt.grid(True)
plt.show()
Here’s a visualization of the test scores against study hours with the best-fit line. The blue points represent the data points (study hours vs. test scores), and the red line is the linear regression model, showing the predicted relationship. This line provides a visual representation of how test scores increase with study hours based on the fitted linear model. Let me know if you need further customization or additional insights
AutoML - TPOT Code
TPOT can explore various preprocessing steps and model configurations, but here, we’ll set it to find the best pipeline that includes linear regression as the primary model for predicting test scores based on study hours.
from tpot import TPOTRegressor
from sklearn.model_selection import train_test_split
import numpy as np
# Sample data: Study hours and corresponding test scores
X = np.array([1, 2, 3]).reshape(-1, 1) # Study hours (independent variable)
y = np.array([2, 3, 5]) # Test scores (dependent variable)
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Initialize TPOT to automate finding the best linear regression model
tpot = TPOTRegressor(generations=5, population_size=20, verbosity=2, random_state=42, config_dict='TPOT sparse')
# Fit the model to the training data
tpot.fit(X_train, y_train)
# Evaluate on test data
print(f"Test score (R^2): {tpot.score(X_test, y_test)}")
# Export the optimized pipeline to Python code
tpot.export('best_pipeline.py')
Explanation of the Code
Data Setup: We use the same dataset as before, with study hours (
X) as the independent variable and test scores (y) as the dependent variable.Data Splitting: We split the dataset into training and testing sets to allow TPOT to optimize based on training data and validate on test data.
TPOT Initialization:
generations=5andpopulation_size=20control the number of optimization cycles.config_dict='TPOT sparse'restricts the search to simpler models (e.g., linear regression).
Model Fitting: TPOT automatically searches for the best model pipeline.
Evaluation and Export: The best model’s performance (R-squared score) is printed, and the optimized pipeline is saved in
best_pipeline.py, which you can inspect and use.
Expected Output
The output would show TPOT’s progress as it searches for the best pipeline. Once completed, you’ll see:
Best Test Score: The R-squared score, showing how well the best pipeline fits the data.
Exported Code:
best_pipeline.pywill contain the optimized pipeline code using Scikit-Learn’sLinearRegressionmodel or a combination of preprocessing steps and model configurations.
Advantages of Using TPOT for Linear Regression
Automation: TPOT automatically searches for the best preprocessing and model configuration.
Optimization: It optimizes hyperparameters to ensure the best performance, even for simple linear models.
Flexibility: TPOT allows the use of various configurations, but with
config_dict='TPOT sparse', we can focus on linear regression.
Subscribe to my newsletter
Read articles from Anix Lynch directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
