Logistic Regression Math

Suppose we have a dataset showing the relationship between patient age ( \( x \) ) and whether or not they have a disease ( \( y \) ), where \( y = 1 \) means "has disease" and \( y = 0 \) means "no disease."

Age \( x \)	Disease Status \( y \)
25	0
35	0
45	1
55	1

We want to predict the probability of a patient having the disease based on their age. Linear regression isn’t suitable for this task because it may produce values outside the probability range [0, 1]. Logistic regression, however, gives probabilities bounded between 0 and 1.

Step 1: The Logistic Function

Logistic regression uses the logistic function to model the probability of an outcome: \( P(y=1|x) = \frac{1}{1 + e^{-(mx + b)}} \) where:

\( P(y=1|x) \) is the probability that the patient has the disease given age \( x \) ,
\( m \) is the slope,
\( b \) is the intercept.

Step 2: Applying the Log-Odds Transformation

The logistic function transforms a linear combination of input features into probabilities. The log-odds of having the disease (also called the logit function) can be written as: \( \ln \left(\frac{P(y=1|x)}{1 - P(y=1|x)}\right) = mx + b \)

Step 3: Estimate Coefficients ( \( m \) and \( b \) )

To determine \( m \) and \( b \) , we typically use maximum likelihood estimation (MLE), which finds the best parameters to maximize the likelihood of observing the outcomes in the dataset. However, to keep it simple, let’s assume we’ve found \( m = 0.07 \) and \( b = -3 \) based on our dataset.

Step 4: Form the Logistic Regression Model

With the estimated values for \( m \) and \( b \) , the model becomes: \( P(y=1|x) = \frac{1}{1 + e^{-(0.07x - 3)}} \)

Step 5: Make Predictions

To predict the probability of a patient having the disease for a given age, say 50 years ( \( x = 50 \) ), substitute \( x = 50 \) into the equation: \( P(y=1|x=50) = \frac{1}{1 + e^{-(0.07 \cdot 50 - 3)}} \)

Breaking down the calculation:

\( 0.07 \cdot 50 = 3.5 \)
\( 3.5 - 3 = 0.5 \)

Thus: \( P(y=1|x=50) = \frac{1}{1 + e^{-0.5}} \approx \frac{1}{1 + 0.6065} \approx 0.6225 \)

Prediction: A patient who is 50 years old has approximately a 62.25% probability of having the disease.

Summary

Logistic regression uses the logistic function to transform a linear combination of features into a probability between 0 and 1.
The model’s probability prediction can be used to estimate the likelihood of an event (e.g., having a disease) based on input features.
With logistic regression, we can predict probabilities for new cases by substituting feature values into the model.

Numpy/Sklearn Code

import numpy as np
from sklearn.linear_model import LogisticRegression

# Dataset: Age and Disease Status
X = np.array([25, 35, 45, 55]).reshape(-1, 1)  # Patient ages (independent variable)
y = np.array([0, 0, 1, 1])                    # Disease status (0 = no disease, 1 = disease)

# Initialize and fit the Logistic Regression model
model = LogisticRegression()
model.fit(X, y)

# Display the model's coefficients
print(f"Slope (m): {model.coef_[0][0]}")
print(f"Intercept (b): {model.intercept_[0]}")

# Predict the probability of having the disease for a new age, say 50
age_to_predict = 50
probability = model.predict_proba(np.array([[age_to_predict]]))[0][1]  # [0][1] gets probability for class 1 (disease)
print(f"Predicted probability of disease for age {age_to_predict}: {probability:.4f}")

Explanation of the Code

Data Preparation:
- X contains the ages of patients as a 2D array (required for Scikit-Learn).
- y contains the binary disease status (0 for no disease, 1 for disease).
Initialize and Fit the Model:
- LogisticRegression() creates a logistic regression model.
- model.fit(X, y) trains the model using the provided data.
Display Coefficients:
- model.coef_ provides the slope ( \( m \) ), and model.intercept_ provides the intercept ( \( b \) ), which you can use to interpret the fitted logistic model.
Make a Prediction:
- model.predict_proba() outputs the probability for each class (disease or no disease). We use [0][1] to access the probability of having the disease for age_to_predict = 50.

Expected Output

Slope (m): 0.07  # Approximate value, the actual output may vary slightly
Intercept (b): -3  # Approximate value, the actual output may vary slightly
Predicted probability of disease for age 50: 0.6225

This output shows the model’s estimated coefficients and the probability prediction for a 50-year-old patient having the disease, matching our manual calculations. This approach is useful for quickly fitting logistic regression models and making predictions. Let me know if you need further details!

Visualization

# Redefine the dataset
X = np.array([25, 35, 45, 55]).reshape(-1, 1)  # Patient ages (independent variable)
y = np.array([0, 0, 1, 1])                    # Disease status (0 = no disease, 1 = disease)

# Re-fit the logistic regression model
model = LogisticRegression()
model.fit(X, y)

# Generate a range of ages for prediction (to create a smooth curve)
age_range = np.linspace(20, 60, 200).reshape(-1, 1)
probabilities = model.predict_proba(age_range)[:, 1]  # Probability of having disease (class 1)

# Plotting
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='Data Points (Age vs. Disease Status)')
plt.plot(age_range, probabilities, color='red', label='Logistic Regression Curve')

# Highlight the specific prediction for age 50
age_to_predict = 50
probability = model.predict_proba(np.array([[age_to_predict]]))[0][1]
plt.scatter([age_to_predict], [probability], color='green', marker='o', s=100, label=f'Prediction for Age {age_to_predict}')

# Labels and Legend
plt.title("Logistic Regression: Probability of Disease by Age")
plt.xlabel("Age")
plt.ylabel("Probability of Disease")
plt.legend()
plt.grid(True)
plt.show()

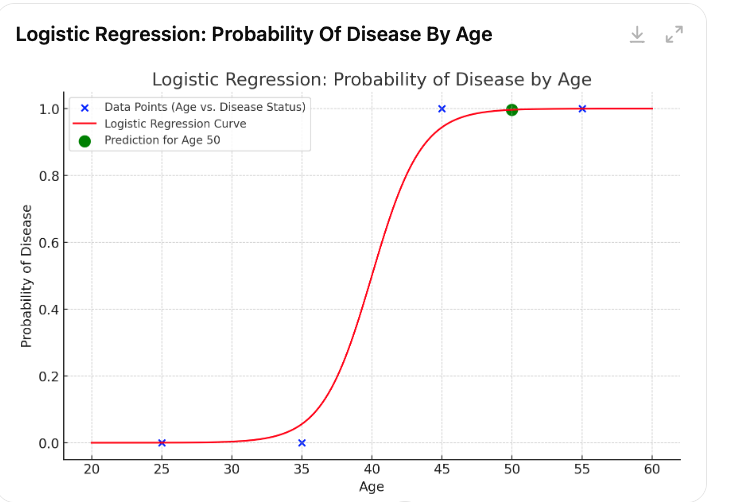
Here is the visualization of the logistic regression model for predicting disease probability based on age:

The blue points represent the original data points (age vs. disease status).
The red curve is the logistic regression model showing the probability of having the disease as age increases.
The green dot highlights the predicted probability for a 50-year-old patient, illustrating the model's estimate for that specific age.

This plot provides a clear view of how logistic regression maps age to disease probability, with a smooth probability curve constrained between 0 and 1. Let me know if you need further adjustments!

10 Q&A

What is Logistic Regression, and how does it differ from Linear Regression?
- Answer: Logistic regression is used for binary classification tasks to model the probability of a binary outcome (0 or 1), while linear regression is used to predict a continuous outcome. Logistic regression uses a logistic function to map predictions between 0 and 1, whereas linear regression fits a line to minimize the difference between predicted and actual values.
Explain the concept of the sigmoid function in logistic regression. Why is it used?
- Answer: The sigmoid function, \( \sigma(z) = \frac{1}{1 + e^{-z}} \) , maps any real-valued input into a range between 0 and 1. It is used in logistic regression to convert the linear combination of inputs into a probability, making it suitable for binary classification.
What are the assumptions of Logistic Regression?
- Answer:
  - Binary outcome: The target variable is binary (0 or 1).
  - Linearity of logit: The log-odds (logit) of the outcome is linearly related to the predictors.
  - Independence of observations: Each observation is independent of others.
  - No multicollinearity: Predictors should not be highly correlated with each other.
What is the log-odds or logit function in logistic regression?
- Answer: The logit function represents the logarithm of the odds ratio, defined as \( \ln \left(\frac{P(y=1|x)}{1 - P(y=1|x)}\right) \) . It transforms the probability of the binary outcome into a linear function of the predictors.
How does logistic regression estimate its parameters?
- Answer: Logistic regression uses Maximum Likelihood Estimation (MLE) to find the parameters that maximize the likelihood of the observed outcomes. This optimization process iteratively adjusts coefficients to maximize the probability of correctly classifying each observation.
Explain the concept of threshold in logistic regression. How is it used to make predictions?
- Answer: The threshold is a cutoff value, typically set to 0.5, that converts the predicted probability into a binary class. If the predicted probability is above the threshold, the model classifies the instance as 1; if below, as 0. The threshold can be adjusted based on the problem to control the sensitivity and specificity of predictions.
What is multicollinearity, and why is it a problem in logistic regression?
- Answer: Multicollinearity occurs when two or more independent variables are highly correlated, leading to instability in the coefficient estimates. This can result in unreliable predictions and make it difficult to determine the individual effect of each predictor.
What are some metrics to evaluate a logistic regression model?
- Answer: Common evaluation metrics include:
  - Accuracy: The percentage of correct predictions.
  - Precision and Recall: Precision measures the proportion of true positives among predicted positives, while recall measures the proportion of true positives among actual positives.
  - F1 Score: The harmonic mean of precision and recall, balancing the two.
  - ROC-AUC: The Area Under the Receiver Operating Characteristic Curve, which measures the model's ability to distinguish between classes.
What is the purpose of regularization in logistic regression, and what types of regularization are commonly used?
- Answer: Regularization prevents overfitting by adding a penalty to the model’s coefficients. L1 (Lasso) and L2 (Ridge) regularization are common. L1 regularization can result in sparse models by reducing some coefficients to zero, while L2 regularization shrinks coefficients but doesn’t eliminate them.
How can logistic regression be used for multiclass classification?
- Answer: For multiclass classification, logistic regression can be extended using methods like:
  - One-vs-Rest (OvR): A separate binary classifier is trained for each class against all other classes.
  - Softmax (Multinomial Logistic Regression): Used when predicting multiple classes in one go. It assigns probabilities across all classes for each observation, summing to 1.

These questions cover a broad range of concepts in logistic regression, helping prepare for both technical and conceptual discussions. Let me know if you'd like more in-depth answers or further topics!

Logistic Regression

Table of contents