Decision Trees
 Anix Lynch
Anix LynchTable of contents
- Step 1: What is a Decision Tree?
- Step 2: Splitting Criteria
- Two Ways to Measure "Good" Splits in a Decision Tree
- Why Use One Over the Other?
- How This Affects the Titanic Tree
- Step 3: Example Calculation of Gini Impurity
- What is "Purity" in Decision Trees?
- Gini Impurity and Purity
- Step 4: Building the Decision Tree
- Step 5: Visualizing the Decision Tree
- Explanation of Each Step:
- Summary of Insights
- Feature Importance Plot
- How to make your decision tree as "pure" (or decisive) as possible?
- 1. Max Depth (max_depth):
- 2. Minimum Samples per Leaf (min_samples_leaf):
- 3. Minimum Samples to Split (min_samples_split):
- 4. Criterion (criterion): Choose between gini and entropy
- Example of a "Pure" Configuration
- Important Note: Balance Purity with Overfitting
- 10 Q&A
Suppose we have a dataset containing information about passengers on the Titanic and whether they survived. The features include class ( \( x_1 \) : Pclass), sex ( \( x_2 \) ), age ( \( x_3 \) ), and fare paid ( \( x_4 \) ). Based on these features, we want to predict whether a passenger survived ( \( y \) , where 1 = survived, 0 = did not survive).
| Pclass \( x_1 \) | Sex \( x_2 \) | Age \( x_3 \) | Fare \( x_4 \) | Survived ( \( y \) ) |
| 3 | 0 (male) | 22 | 7.25 | 0 |
| 1 | 1 (female) | 38 | 71.28 | 1 |
| 3 | 1 (female) | 26 | 7.92 | 1 |
| 1 | 1 (female) | 35 | 53.10 | 1 |
| 3 | 0 (male) | 35 | 8.05 | 0 |
We use a Decision Tree to classify passengers as "survived" or "did not survive" based on these features.
Step 1: What is a Decision Tree?
A decision tree is a structure where:
Nodes represent features or attributes in the dataset.(ie. Sex)
Branches represent conditions based on those features (ie Sex = female)
Leaves represent the final prediction (e.g., survived or not survived).
The tree recursively splits the data based on the feature that best separates the data, chosen using criteria such as Gini Impurity or Information Gain.
Step 2: Splitting Criteria
Gini Impurity
\( \text{Gini} = 1 - \sum p_i^2 \) where \( p_i \) is the probability of a particular class in a node.
Information Gain
\( \text{Entropy} = - \sum p_i \log_2(p_i) \) Higher Information Gain is preferred as it indicates a better split.
Absolutely, let’s make this simple.
Two Ways to Measure "Good" Splits in a Decision Tree
When building a decision tree, we want each split (or decision point) to divide the data into groups that are as "pure" as possible. Purity here means that each group has mostly one type of result (e.g., mostly "Survived" or mostly "Not Survived" passengers in the Titanic case). There are two main ways to measure how "pure" a split is:
Gini Impurity:
Gini Impurity is a measure of how mixed a group is.
A low Gini value means the group is mostly one type (either "Survived" or "Not Survived").
A high Gini value means a mix of types (like 50% "Survived" and 50% "Not Survived").
In simple terms: Gini wants each split to make groups as pure as possible, minimizing the mix of different results in each group.
Information Gain (using Entropy):
Information Gain looks at how much "disorder" there is in a group.
Entropy is high when the group is very mixed (e.g., 50-50 "Survived" and "Not Survived") - or can’t make decision in decision tree!
The goal is to choose splits that reduce entropy, so each group becomes more uniform.
In simple terms: Information Gain looks for splits that create less messy groups, making each one lean more toward a single outcome.
Why Use One Over the Other?
Gini Impurity is simple and fast, so it’s commonly used, especially when speed matters. That’s why the Titanic example uses Gini by default.
Information Gain (Entropy) can sometimes be a bit more sensitive to different class balances, so it’s useful when you have uneven distributions (like 90% "Survived" vs. 10% "Not Survived").
How This Affects the Titanic Tree
If you want the tree to split based on Information Gain instead of Gini Impurity, you can adjust the tree settings. This might lead to slightly different splits in the tree, as it’ll look for splits that reduce "disorder" instead of "mix."
Code to Switch to Information Gain:
from sklearn.tree import DecisionTreeClassifier
# Set the tree to use Information Gain (entropy) instead of Gini Impurity
tree_model = DecisionTreeClassifier(max_depth=3, criterion="entropy", random_state=42)
tree_model.fit(X, y)
In summary:
Gini: Quick, aims for splits that make groups mostly one type.
Information Gain: Looks for splits that reduce messiness in the group.
Step 3: Example Calculation of Gini Impurity
Suppose we start with a node containing passengers with survival labels: \(\text{Not Survived}, \text{Survived}, \text{Survived}, \text{Survived}\).
Calculate Gini Impurity:
* Probability of Survived ( \( p_{\text{survived}} \) ) = 3/4
* Probability of Not Survived ( \( p_{\text{not survived}} \) ) = 1/4
* Gini = \( 1 - (p_{\text{survived}}^2 + p_{\text{not survived}}^2) = 1 - ((3/4)^2 + (1/4)^2) = 0.375 \)
A split that minimizes Gini Impurity or maximizes Information Gain is chosen.
What is "Purity" in Decision Trees?
Pure Node: A node is pure if it contains data points that all belong to the same category (e.g., all "Survived" or all "Not Survived").
Impure Node: A node is impure if it contains a mix of categories (e.g., some "Survived" and some "Not Survived").
Gini Impurity and Purity
Lower Gini Impurity (closer to 0): Means the node is purer (mostly one category, like all "Survived").
Higher Gini Impurity (closer to 0.5): Means the node is more mixed (a more even mix of "Survived" and "Not Survived").
In decision trees, we aim for purer nodes because they give clearer predictions.
Step 4: Building the Decision Tree
Using our Titanic dataset, the decision tree algorithm will:
Choose the best feature (e.g., Sex) to split the data, based on Gini Impurity or Information Gain.
Continue splitting until pure leaf nodes or a maximum depth is reached, creating branches that lead to the final prediction.
Example Splits
Split by Sex: If \( \text{Sex} = 1 \) (female), the passenger is more likely to have survived.
Split by Age: For male passengers, a further split might be based on age, with younger passengers having a slightly higher chance of survival.
Step 5: Visualizing the Decision Tree
Using the determined splits, we can visualize the decision-making process for the Titanic dataset.
# Import necessary libraries
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier, plot_tree
# Load the Titanic dataset (make sure to have 'train.csv' in the same directory)
titanic_train = pd.read_csv('train.csv')
# Data Preprocessing
# Drop columns that are not useful for prediction
titanic_train = titanic_train.drop(['PassengerId', 'Name', 'Ticket', 'Cabin'], axis=1)
# Fill missing values
titanic_train['Age'].fillna(titanic_train['Age'].median(), inplace=True)
titanic_train['Embarked'].fillna(titanic_train['Embarked'].mode()[0], inplace=True)
# Convert categorical columns to numeric
titanic_train['Sex'] = titanic_train['Sex'].map({'male': 0, 'female': 1})
titanic_train['Embarked'] = titanic_train['Embarked'].map({'S': 0, 'C': 1, 'Q': 2})
# Create a new feature 'FamilySize' (optional feature for experimentation)
titanic_train['FamilySize'] = titanic_train['SibSp'] + titanic_train['Parch']
# Define features and target variable
X = titanic_train[['Pclass', 'Sex', 'Age', 'Fare', 'FamilySize']]
y = titanic_train['Survived']
# Initialize and train the decision tree classifier
tree_model = DecisionTreeClassifier(max_depth=3, criterion="gini", random_state=42)
tree_model.fit(X, y)
# Plotting the decision tree
plt.figure(figsize=(16, 10))
plot_tree(tree_model, feature_names=X.columns, class_names=["Not Survived", "Survived"],
filled=True, rounded=True)
plt.title("Decision Tree for Titanic Survival Prediction")
plt.show()
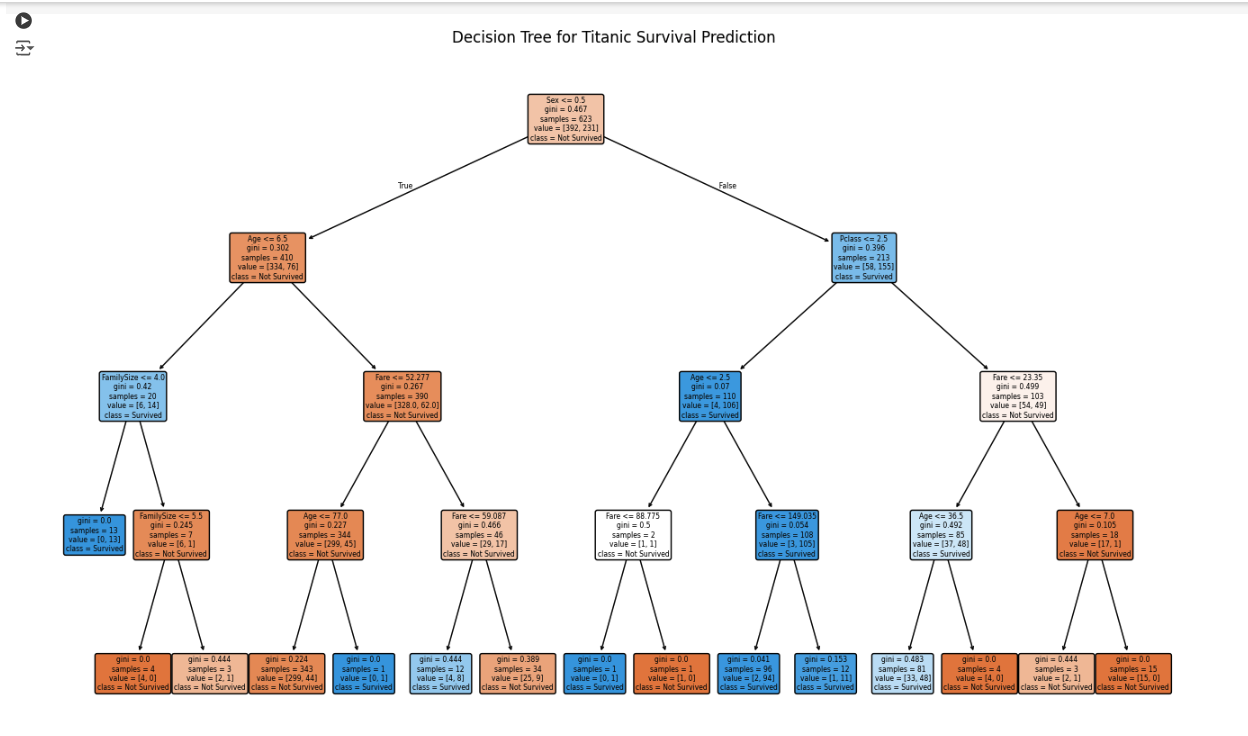
The colors in the decision tree visualization usually represent the predicted class and the level of certainty:
Color of the Node:
Orange typically represents one class (e.g., "Not Survived" in the Titanic example).
Blue represents the other class (e.g., "Survived").
Shade Intensity:
Darker colors (dark orange or dark blue) indicate a purer node where most data points belong to the same class. This means the model is more confident in the prediction for that node.
Lighter colors (light orange or light blue) indicate a more mixed node, where there’s less certainty. This happens when the node contains a mix of both classes, even if one is slightly dominant.
In summary:
Darker colors = higher certainty (more pure nodes).
Lighter colors = lower certainty (more mixed nodes).
Explanation of Each Step:
Load the Dataset: Reads the Titanic dataset from a CSV file.
Data Preprocessing:
Drops columns that are not directly relevant to the prediction (
PassengerId,Name,Ticket,Cabin).Fills missing values in the
AgeandEmbarkedcolumns with the median and mode, respectively.Converts categorical values (
SexandEmbarked) to numeric representations.Creates a new feature
FamilySizeby combiningSibSpandParchto represent family size.
Define Features and Target: Selects
Pclass,Sex,Age,Fare, andFamilySizeas features andSurvivedas the target variable.Train the Model: Initializes and trains a decision tree classifier with a maximum depth of 3.
Plot the Tree: Visualizes the decision tree structure with nodes filled and rounded, showing the decision-making process.
This code will produce a decision tree plot for the Titanic dataset, showing key splits based on features such as Sex, Pclass, Age, etc., and can help interpret which factors most influence survival predictions.
|--- Age <= 6.50
| |--- FamilySize <= 4.00
| | |--- class: Survived
| |--- FamilySize > 4.00
| | |--- class: Not Survived
|--- Age > 6.50
| |--- Sex <= 0.50
| | |--- Fare <= 52.28
| | | |--- class: Not Survived
...
Summary of Insights
By combining feature importance and decision rules, you can summarize the main insights without needing to interpret the entire tree structure:
Top Influential Features: Check the top features based on feature importance (e.g.,
Sex,Pclass,Age).Key Decision Rules: Use the extracted rules to see common paths leading to survival or non-survival. For example, rules might indicate that:
Females with higher class and age under a certain threshold are likely to survive.
Males with lower fares and lower-class tickets are more likely to not survive.
Using these methods, you get a clear summary of what the decision tree model "learned" about survival on the Titanic without manually reading the tree visualization.
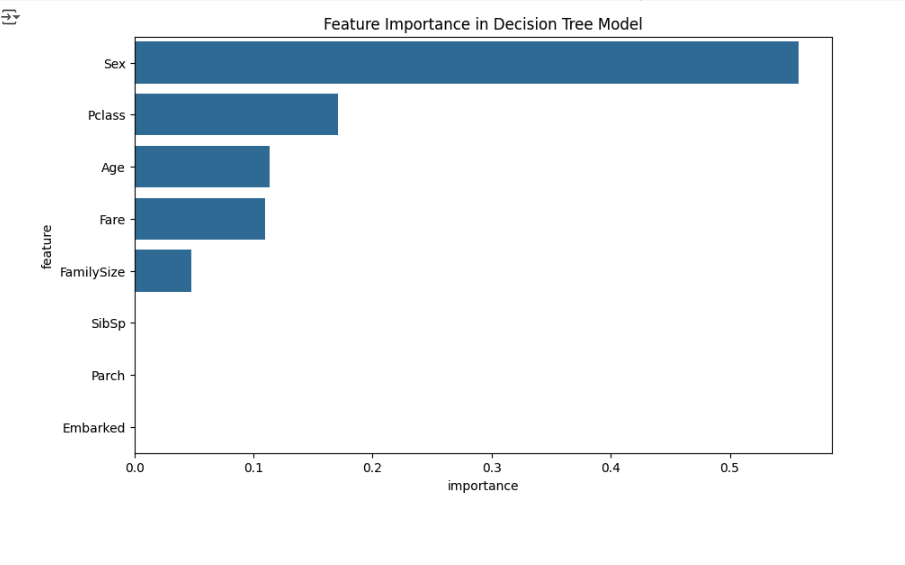
Feature Importance Plot
```python import matplotlib.pyplot as plt import seaborn as sns
# Get feature importances from the model importances = tree_model.feature_importances_ feature_names = X.columns
# Create a DataFrame for better visualization feature_importances = pd.DataFrame({'feature': feature_names, 'importance': importances}) feature_importances = feature_importances.sort_values(by='importance', ascending=False)
# Plot the feature importance plt.figure(figsize=(10, 6)) sns.barplot(x='importance', y='feature', data=feature_importances) plt.title("Feature Importance in Decision Tree Model") plt.show() ```
Feature importance tells you which features have the most influence on the model's predictions. This can help you understand what factors are most important for survival.
### Summary of Insights
By combining feature importance and decision rules, you can summarize the main insights without needing to interpret the entire tree structure:
1. Top Influential Features: Check the top features based on feature importance (e.g., Sex, Pclass, Age).
2. Key Decision Rules: Use the extracted rules to see common paths leading to survival or non-survival. For example, rules might indicate that:
* Females with higher class and age under a certain threshold are likely to survive.
* Males with lower fares and lower-class tickets are more likely to not survive.
Using these methods, you get a clear summary of what the decision tree model "learned" about survival on the Titanic without manually reading the tree visualization.
How to make your decision tree as "pure" (or decisive) as possible?
You can adjust a few key parameters. Here’s how:
1. Max Depth (max_depth):
This controls how many levels the tree can grow.
Lower max depth: The tree stops early, which can lead to less purity but helps avoid overfitting.
Higher max depth: The tree can grow deeper, splitting until nodes are as pure as possible (or other stopping criteria are met).
Tip: Start with a reasonable depth (like 3-5), then increase if you need more purity.
tree_model = DecisionTreeClassifier(max_depth=10) # Set to a higher number to allow more splits
2. Minimum Samples per Leaf (min_samples_leaf):
This sets the minimum number of samples a leaf (final node) should have.
Smaller value: Allows more splits, leading to purer nodes but can also overfit.
Larger value: Stops splitting sooner, which can result in less pure but more generalized nodes.
Tip: A small value like 1 or 2 allows the tree to keep splitting, but it may lead to overfitting.
tree_model = DecisionTreeClassifier(min_samples_leaf=1) # Setting this low allows high purity
3. Minimum Samples to Split (min_samples_split):
This controls the minimum number of samples required to split a node.
Smaller value: Allows more splits, increasing purity but also risk of overfitting.
Larger value: Prevents splitting too much, which can lead to less purity.
Tip: Setting it low (like 2) allows splitting to continue, making nodes as pure as possible.
tree_model = DecisionTreeClassifier(min_samples_split=2) # Allows many splits for high purity
4. Criterion (criterion): Choose between gini and entropy
Gini: Faster and often effective in binary splits.
Entropy: Often achieves slightly purer nodes but is slower.
Tip: Use
entropyif you want to focus on purity, as it can sometimes result in purer splits.
tree_model = DecisionTreeClassifier(criterion="entropy")
Example of a "Pure" Configuration
Here’s how you could configure the parameters to make a tree as pure as possible. Be aware that this setup could lead to overfitting because it tries to split until the nodes are very pure, potentially memorizing the training data.
from sklearn.tree import DecisionTreeClassifier
tree_model = DecisionTreeClassifier(
max_depth=10, # Allowing deep splits
min_samples_leaf=1, # Allowing nodes with a single sample to be a leaf
min_samples_split=2, # Allowing frequent splits
criterion="entropy" # Using entropy to aim for higher purity
)
tree_model.fit(X, y)
Important Note: Balance Purity with Overfitting
When aiming for purity, be careful. A tree that is too deep or splits too often can memorize the training data (overfitting), leading to poor performance on new data. Use cross-validation or test data to check if your tree is generalizing well and not just becoming extremely pure on the training data alone.
Here are 10 interview questions related to decision trees that are commonly asked in data science interviews:
10 Q&A
Explain how a decision tree works.
- Answer: A decision tree is a flowchart-like structure where each internal node represents a decision on a feature, each branch represents the outcome of the decision, and each leaf node represents a class label (or a decision outcome). The tree is built by recursively splitting data to maximize purity in each node based on certain criteria like Gini impurity or information gain.
What are some common metrics used to split nodes in a decision tree?
Answer: Common metrics include:
Gini Impurity: Measures how often a randomly chosen element from the set would be incorrectly classified.
Entropy / Information Gain: Measures the amount of disorder or impurity in a node. The split is chosen to maximize information gain (decrease in entropy).
Mean Squared Error (MSE): Used for regression tasks, it measures the average squared difference between predicted and actual values.
What is overfitting in decision trees, and how can it be prevented?
Answer: Overfitting occurs when a decision tree learns the noise in the training data, resulting in poor generalization to new data. This can be prevented by:
Pruning: Cutting off branches that have little importance.
Setting a maximum depth: Limiting how deep the tree can grow.
Setting a minimum samples split: Limiting the minimum number of samples needed to split a node.
What is pruning, and why is it used in decision trees?
- Answer: Pruning is the process of removing sections of the tree that provide little power in predicting the target variable. Pruning reduces the size of the decision tree, thereby preventing overfitting and improving the model's generalization.
How does a decision tree handle missing values?
Answer: Decision trees can handle missing values in several ways, depending on the implementation:
Ignoring rows with missing values.
Using surrogate splits: Finding alternative features to make the split if the primary feature has missing values.
Using mean, median, or mode imputation.
What are some advantages and disadvantages of decision trees?
Advantages:
Easy to understand and interpret.
Handles both numerical and categorical data.
Requires little data preprocessing.
Disadvantages:
Prone to overfitting, especially with deep trees.
Sensitive to changes in the data (high variance).
Can be biased towards features with more levels.
Explain the difference between a classification tree and a regression tree.
- Answer: A classification tree is used for categorical target variables, splitting nodes based on measures like Gini or entropy to create classes. A regression tree is used for continuous target variables, splitting nodes to minimize the mean squared error (MSE) in the predicted values.
What is the difference between Gini Impurity and Entropy in decision trees?
Answer: Both are metrics used to decide splits in decision trees:
Gini Impurity: Measures the probability of incorrectly classifying a random element. It ranges from 0 (pure node) to 0.5 for binary classes.
Entropy: Measures the level of uncertainty or impurity in a node, ranging from 0 (pure node) to 1 for binary classes. While both are used to determine node splits, Gini is generally faster to compute.
What are surrogate splits, and when are they used in decision trees?
- Answer: Surrogate splits are used to handle missing values. When the primary split feature has missing values, surrogate splits use other features that correlate with the primary split feature to make decisions, allowing the tree to handle missing data more effectively.
When would you choose a decision tree over other algorithms like logistic regression or SVM?
Answer: A decision tree might be preferred when:
Interpretability is crucial (e.g., when you need to explain the model to stakeholders).
There are complex non-linear relationships among features.
The dataset contains a mix of numerical and categorical features.
You want a model that can automatically perform feature selection.
Subscribe to my newsletter
Read articles from Anix Lynch directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
