Exploring Algorithm Complexity: The Basics of Big O Notation

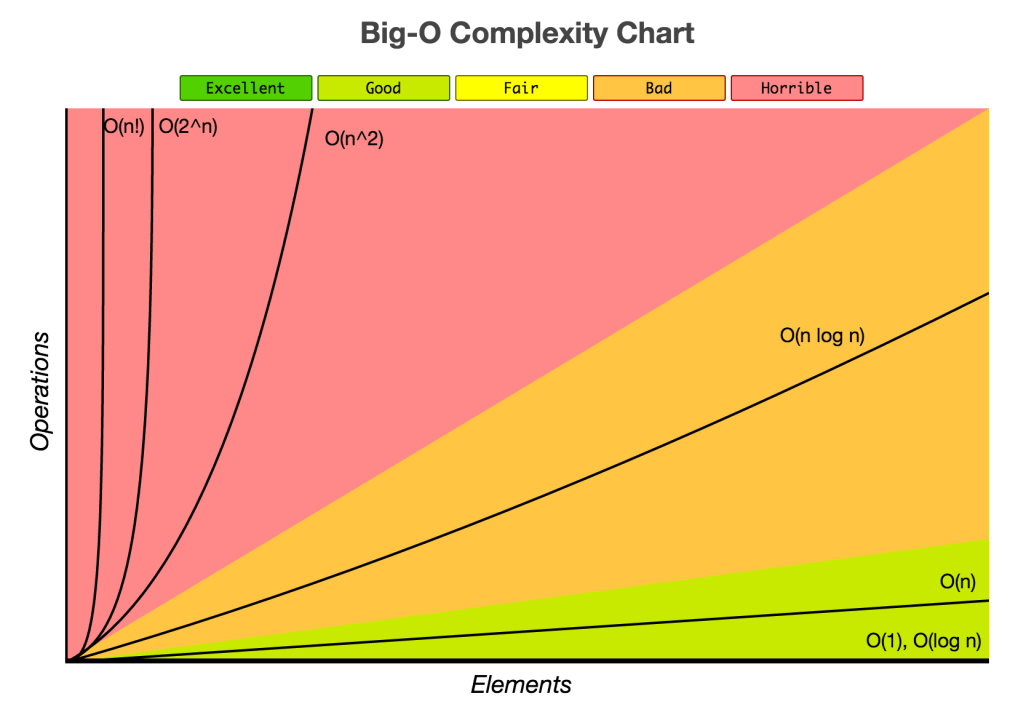
When evaluating the performance of algorithms, one of the most common ways to describe how they behave as the input size increases is by using Big O notation. Here are some of the most common runtime complexities explained:

Constant Time Complexity - O(1)

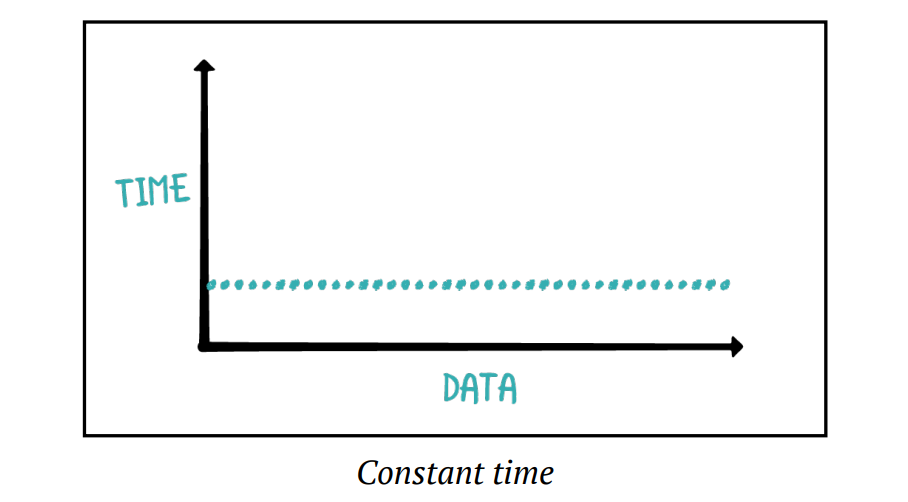
Constant time complexity is denoted as O(1). This means that the running time of the algorithm remains constant regardless of how large the input size grows. Whether you're working with 10 elements or 10 million elements, it performs the same operation consistently without any increase in execution time.

Logarithmic Time Complexity - O(log n)

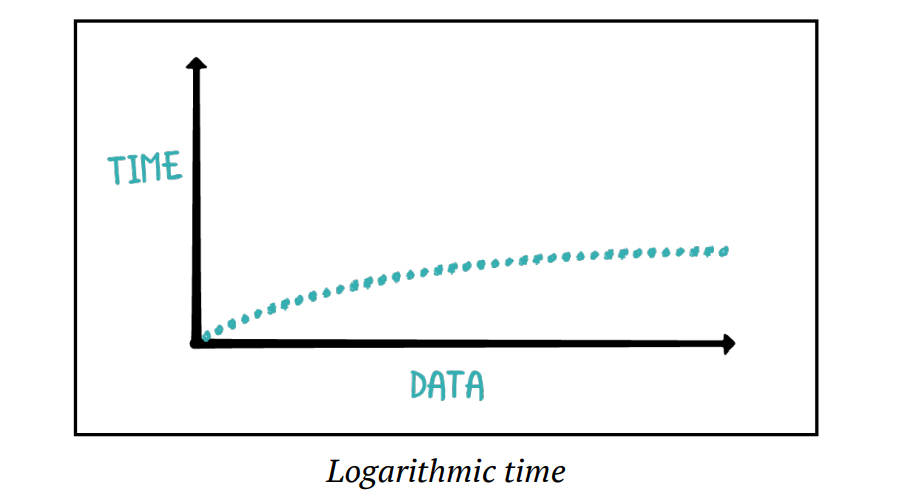
Logarithmic time complexity indicates that the algorithm halves the data set at each step. On a graph, it appears close to the constant time complexity curve. For example, in an array with 100 elements, such an algorithm might only take 10 or 11 steps to find a target element. A classic example of this is the Binary Search algorithm, which repeatedly divides the list in half until the desired element is found. As the input size grows, the time taken by a logarithmic complexity algorithm grows slowly due to the way it divides the problem.

Linear Time Complexity - O(n)

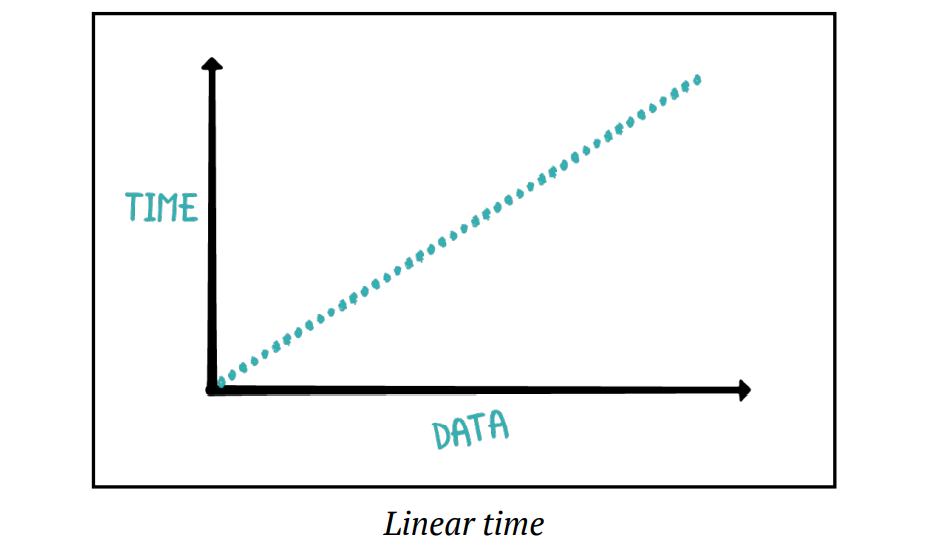
Linear time complexity, denoted as O(n), is the most common time complexity. The running time grows linearly with the size of the input. Simply put, if the input size doubles, the time required to process it also doubles.

Quadratic Time Complexity - O(n²)

In quadratic time complexity, the runtime increases quadratically as the input size grows. Algorithms with this complexity often involve nested loops.

Cubic Time Complexity - O(n³)

With cubic time complexity, the runtime grows cubically with the size of the input data. As you can guess, this becomes impractical for even moderately large inputs.

Polynomial Time Complexity - O(n^k)

Polynomial time complexity, denoted as O(n^k), describes algorithms where the running time is proportional to the input size raised to a constant power, k. Examples include O(n), O(n²), O(n³), and so on. While polynomial time algorithms are generally considered efficient for small to medium-sized inputs, they can become impractical as input sizes grow.

Quasilinear Time Complexity - O(n log n)

This runtime complexity is a bit worse than linear complexity but significantly better than polynomial complexity. Examples include efficient sorting algorithms like Merge Sort and Quick Sort.

Exponential Time Complexity - O(2^n)

Exponential time complexity occurs when a small increase in input size causes a dramatic increase in runtime. For example, every additional input doubles the number of steps needed. This is common in many recursive algorithms, such as the naive approach to generating Fibonacci numbers or solving the Towers of Hanoi problem. While these algorithms may be simpler to implement, they become inefficient with large inputs.

Factorial Time Complexity - O(n!)

The factorial time complexity describes an extremely high growth rate and occurs when an algorithm performs n! operations (e.g., n × (n-1) × (n-2) × ... × 1). This is typical of brute-force algorithms, such as solving the traveling salesman problem using brute force. For even moderately-sized inputs, this complexity quickly becomes impractical.