Dans le cadre de l'analyse prédictive en immobilier, j'ai entrepris un projet visant à estimer les prix des maisons en utilisant des techniques de machine learning. Ce projet s'appuie sur le dataset "USA Housing", qui fournit diverses informations sur les propriétés résidentielles aux États-Unis.

Références du projet

Dataset : Data

Notebook : Predicting House Prices

Directory : Housing

Objectif du Projet

L'objectif principal est de développer un modèle capable de prédire avec précision le prix de vente d'une maison en fonction de plusieurs caractéristiques, telles que le revenu moyen de la zone, l'âge moyen des maisons, le nombre moyen de pièces et de chambres, ainsi que la population de la zone.

Exploration des Données

df.head()

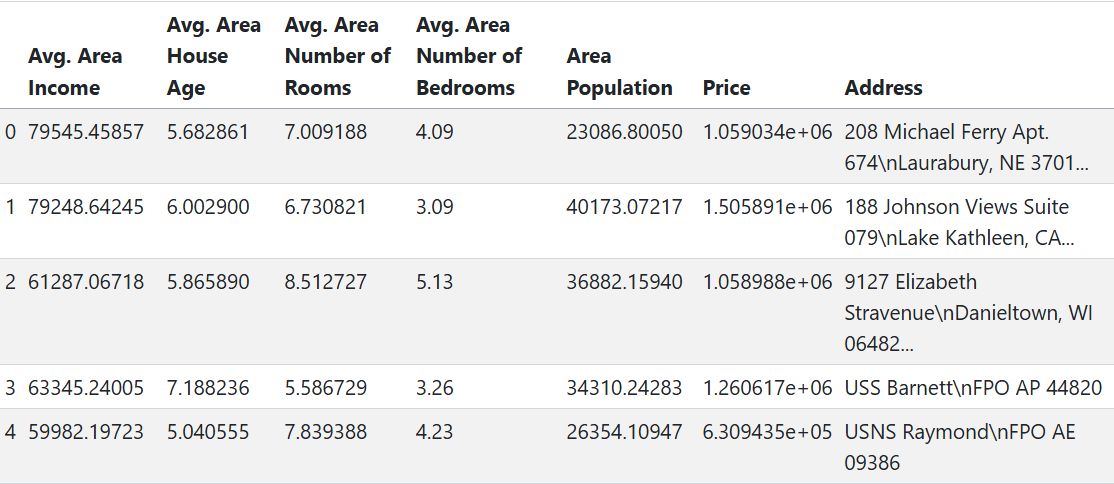
Le dataset comprend 5 000 enregistrements et 7 colonnes :

Avg. Area Income : Revenu moyen des résidents de la zone.
Avg. Area House Age : Âge moyen des maisons dans la zone.
Avg. Area Number of Rooms : Nombre moyen de pièces par maison.
Avg. Area Number of Bedrooms : Nombre moyen de chambres par maison.
Area Population : Population de la zone.
Price : Prix de vente de la maison.
Address : Adresse de la maison.

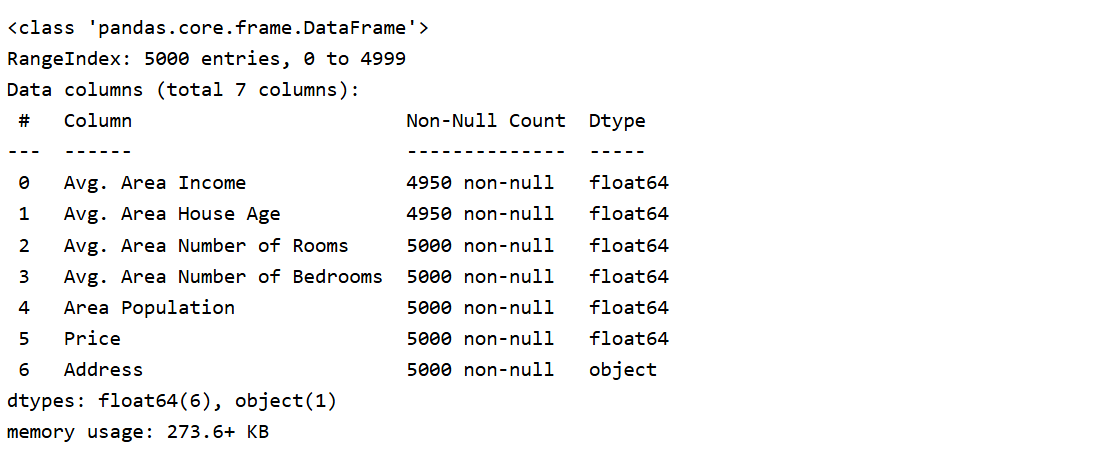
Une analyse initiale a révélé que les colonnes "Avg. Area Income" et "Avg. Area House Age" contiennent chacune 10 valeurs manquantes. Les autres colonnes sont complètes.

df.info()

Analyse Statistique Descriptive

Les statistiques descriptives montrent que le prix moyen des maisons est d'environ 1 232 073 $, avec une variation significative allant de 15 939 $ à 2 469 066 $. Les maisons ont en moyenne 7 pièces et près de 4 chambres, avec un âge moyen d'environ 6 ans. Le revenu moyen des zones est de 68 564 $, et la population moyenne est d'environ 36 914 habitants.

Visualisation des données

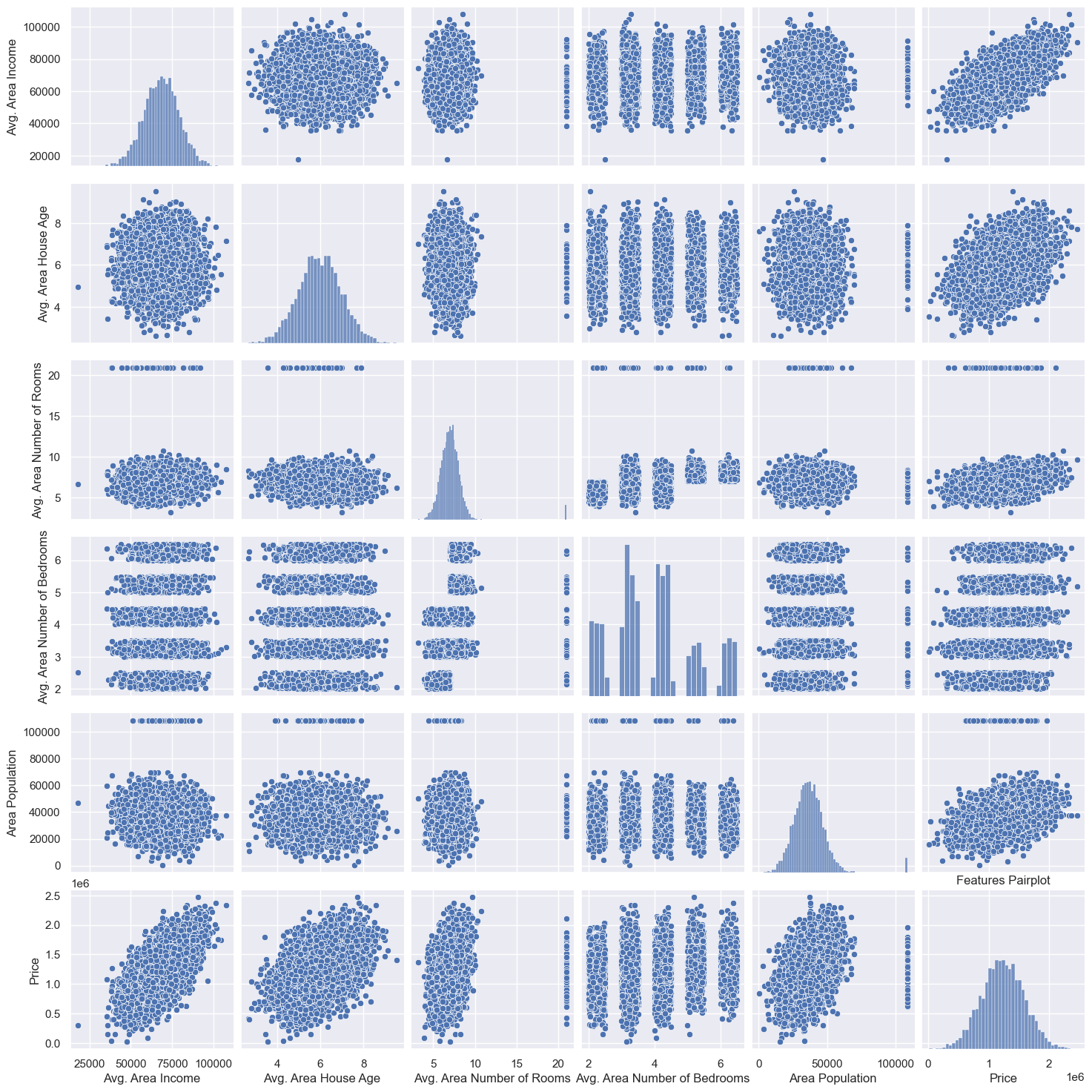
Ce pairplot révèle la présence de valeurs aberrantes dans certaines variables (nombre de pièces et population), avec des valeurs largement au-delà de la norme, ce qui pourrait biaiser l’analyse et nécessite un examen attentif ou un ajustement.

Ensuite, en analysant la relation entre le prix et les autres caractéristiques des logements, on constate que :

Prix vs. Revenu Moyen de la Zone : Il existe une relation positive entre le prix et le revenu moyen de la zone, ce qui suggère que les zones avec des revenus plus élevés ont des prix de logements plus élevés.
Prix vs. Nombre Moyen de Pièces : On observe une légère tendance positive : les maisons avec plus de pièces tendent à être plus chères.
Prix vs. Population de la Zone : On observe une relation positive entre le prix et la population de la zone, indiquant que la densité de population est pas un facteur déterminant pour les prix, d'autres éléments comme le revenu et les commodités jouant probablement un rôle plus important.

Préparation des Données

Avant de construire le modèle, il est essentiel de traiter les valeurs manquantes et de normaliser les données pour assurer une performance optimale du modèle. Des techniques telles que l'imputation des données manquantes et la normalisation des variables numériques ont été appliquées à partir d’une pipeline ci-dessous.

import pandas as pd
import numpy as np
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
import pickle

def preprocess(df, train):
    """
    This function handles missing and aberrant (outlier) values in a DataFrame by replacing them with the median of the respective column's distribution.
    It also applies scaling to standardize the data.

    Args:
        df (DataFrame): The dataset containing columns with missing or aberrant values.
        train (bool): A flag indicating whether the function is being applied to a training set (True) or a test set (False).
                      If True, the function will fit and save an imputer, scaler, and outlier bounds; if False, it will load and apply the saved models and bounds.

    Returns:
        DataFrame: A transformed DataFrame with missing and aberrant values replaced by the median, and features standardized.

    Process:
        1. Outlier Detection and Replacement: Outliers are identified using the IQR (Interquartile Range) method.
           Values below Q1 - 1.5*IQR or above Q3 + 1.5*IQR are considered outliers and replaced with NaN.
        2. Imputation: Missing values (including outliers replaced by NaN) are filled with the median of each column.
           If train is True, an imputer is fit and saved for later use. If train is False, the previously saved imputer is loaded.
        3. Scaling: Standardizes the data to have a mean of 0 and a standard deviation of 1.
           If train is True, a scaler is fit and saved; otherwise, the saved scaler is loaded and applied.
    """

    # Step 1: Handle outliers based on the IQR method
    if train:
        # Calculate and save outlier bounds for each column in the training data
        outlier_bounds = {}
        for col in df.columns:
            Q1 = df[col].quantile(0.25)
            Q3 = df[col].quantile(0.75)
            IQR = Q3 - Q1
            lower_bound = Q1 - 1.5 * IQR
            upper_bound = Q3 + 1.5 * IQR
            outlier_bounds[col] = (lower_bound, upper_bound)

            # Replace outliers with NaN in training data
            df.loc[(df[col] < lower_bound) | (df[col] > upper_bound), col] = np.nan

        # Save the outlier bounds
        with open('outlier_bounds.pickle', 'wb') as f:
            pickle.dump(outlier_bounds, f)
    else:
        # Load and apply outlier bounds in the test data
        with open('outlier_bounds.pickle', 'rb') as f:
            outlier_bounds = pickle.load(f)

        for col in df.columns:
            lower_bound, upper_bound = outlier_bounds[col]
            df.loc[(df[col] < lower_bound) | (df[col] > upper_bound), col] = np.nan

    # Step 2: Impute missing values with the median
    if train:
        imputer = SimpleImputer(strategy='median')
        imputer.fit(df)
        with open('imputer.pickle', 'wb') as f:
            pickle.dump(imputer, f)
    else:
        with open('imputer.pickle', 'rb') as f:
            imputer = pickle.load(f)

    df = pd.DataFrame(imputer.transform(df), columns=df.columns)

    # Step 3: Standardize the data
    if train:
        scaler = StandardScaler()
        scaler.fit(df)
        with open('scaler.pickle', 'wb') as f:
            pickle.dump(scaler, f)
    else:
        with open('scaler.pickle', 'rb') as f:
            scaler = pickle.load(f)

    df = pd.DataFrame(scaler.transform(df), columns=df.columns)

    return df

Modélisation

Plusieurs algorithmes de machine learning ont été explorés pour prédire les prix des maisons, notamment :

Régression Linéaire : Modèle simple qui tente de trouver la relation linéaire entre les variables indépendantes et le prix.
K-Nearest Neighbors (KNN) : Algorithme qui prédit le prix d'une maison en se basant sur les prix des maisons les plus proches dans l’espace des variables. Il utilise la distance entre les points pour identifier les "voisins" et estime le prix en moyenne des valeurs proches.

Chaque modèle a été évalué en utilisant des métriques telles que la Mean Squared Error (MSE) et le coefficient de détermination (R²) pour déterminer sa performance prédictive.

Résultats

Les performances des modèles sont les suivantes :

Régression Linéaire : MSE moyen de 15350399432.8 avec un R² de 86%.
KNN : MSE moyen de 22565570117.23 avec un écart-type de 75%.

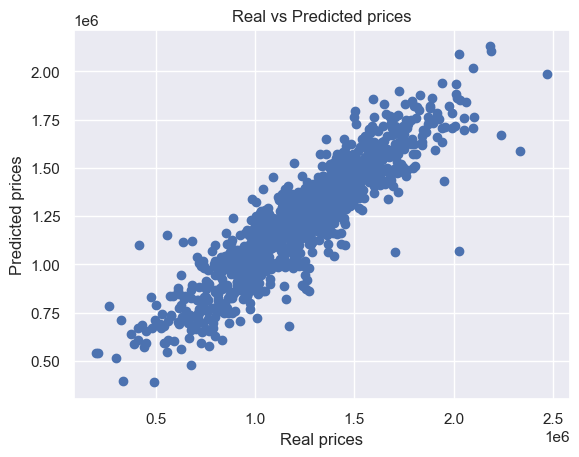
Ces résultats montrent que la Régression Linéaire offre la meilleure performance prédictive parmi les modèles testés. Cependant, son MSE élevé révèle des limitations importantes. Ce qui signifie qu'il est possible d'améliorer encore la précision du modèle.

Conclusion

Dans cette étude, deux modèles prédictifs, la régression linéaire et K-Nearest Neighbors (KNN), ont été testés pour estimer les prix des maisons. La régression linéaire a obtenu un R² d'environ 86%, indiquant une bonne explication de la variance des prix, bien que le MSE reste élevé, signalant des limites. KNN a présenté un R² plus faible de 75%, montrant une moins bonne adéquation aux données.

La régression linéaire s'est avérée plus efficace, capturant mieux la variance des prix avec une meilleure précision et interprétabilité.

Des modèles plus complexes ou un travail de feature engineering pourraient être envisagés pour améliorer les résultats.

Pour une exploration plus détaillée et le code source complet, vous pouvez consulter le repository du projet sur Github (HOUSING).

Merci et enjoy !🎉

House Prices Prediction

Table of contents