Union Find Algorithm(Graph Theory)- Beginner friendly explanation

If you are learning about graphs, then there is one thing that u must keep in your mind, that everything will not be understandable in a single go. Visualization helps a lot. But these concepts are essential in DSA point of view, if you are trying to get placed in a good product based company.

• The word Union Find algorithm aka disjoint set union(DSU) might sound complex, but it is easy to comprehend.

• It can be broken down into 2 simple functions namely Union and Find. Find: For a given value say x, it is used to find which set it belongs to. Union: For two sets given say x1 and x2 , it performs the union operation.

• Python coding explanation is given for easy understanding.

Lets get into the technical side of this, this algorithm uses two lists namely par and rank.

def __init__(self, n):
    self.par = [i for i in range(n)] #stores the parent of every element
    self.rank = [1] * n #stores the height of that element in graph

Initially, for every element i, it is its own parent. So par stores values as [0,1, …,n-1]. Rank is initialized as 1 for every element because each element in its own, makes a height of 1 .

Now lets define the Find function: Find is used to find the leader or the root of the set that ‘x’ belongs to.

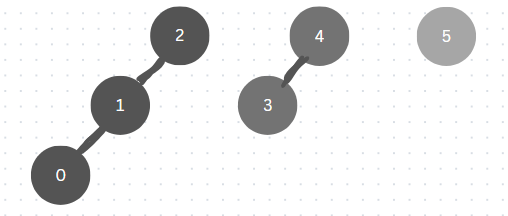
Lets take an example, given below which represents connected components:

def find(self, x):
    while x != self.par[x]:
        self.par[x] = self.par[self.par[x]] #path compression
        x = self.par[x]
    return x

The par list will look like this before find function: [1,2,2,4,4,5] where each element points to its parent or the leader.

Lets call the find(0), the root of 0 is 2 so now the par is updated as [2,2,2,4,4,5]. This code uses path compression to make future queries faster: as it moves up the tree to find the root, it compresses the path by pointing each visited node directly to the root.

Calling find(1) ,find(2),find(3) ,find(4) and find(5) the par remains the same because it is already pointing to the root. Note that for the root element, its root is itself.

Now lets define the Union Function:

def union(self, x1, x2):
    p1, p2 = self.find(x1), self.find(x2)
    if p1 == p2:
        return False
    if self.rank[p1] > self.rank[p2]:
        self.par[p2] = p1
        self.rank[p1] += self.rank[p2]
    else:
        self.par[p1] = p2 
        self.rank[p2] += self.rank[p1]
    return True

It is used to join two sets together, if the two sets have the same root, we return false because there is no need of joining as they belong to the same set.p1 and p2 represent the roots of elements x1 and x2 found using find function.

The union is applied only if they belong to different sets. The union is done by rank. If the rank of p1 is higher than the p2, then the parent of p2 points to the root of the p1 and the rank of p1 is updated by adding the rank of p1 . It simple means that the shorter tree is attached with the larger tree.

Why do we need this algorithm?

The Union-Find algorithm efficiently manages and tracks connected components in a graph, allowing quick merging and checking of connections. It is essential for problems like detecting cycles, finding minimum spanning trees, and dynamic connectivity.