TLDR: If p-value > 0.05: This means the difference could just be random, so we say there’s no significant effect

Use Case:

• A/B Testing for Marketing: You want to see if a new ad brings in more clicks than the old one. So, you compare the average clicks, using the t-test to check if the difference is real: \( H_0: \mu_{\text{new}} = \mu_{\text{old}} \) .

• Medical Trials: Testing if a new drug works better than a placebo by comparing average recovery times. The t-test tells us if any improvement is likely from the drug or just random chance: \( H_0: \mu_{\text{drug}} = \mu_{\text{placebo}} \) .

• Product Quality Control: You’re checking if two batches of a product are consistent in weight. The t-test helps decide if any difference is due to manufacturing or just natural variation: \( H_0: \mu_{\text{batch1}} = \mu_{\text{batch2}} \) .

• User Engagement in Apps: Seeing if users spend more time on a redesigned app. The t-test helps you figure out if the redesign actually boosted engagement: \( H_0: \mu_{\text{new design}} = \mu_{\text{old design}} \) .

• Student Performance: Comparing two teaching methods by looking at test scores from each group. The t-test tells you if one method truly led to higher scores or if it’s just a fluke: \( H_0: \mu_{\text{method1}} = \mu_{\text{method2}} \) .

---

Define Hypotheses:

• Null Hypothesis (H₀): The drug has no effect, meaning the average results of the Control and Drug groups are the same: \( H_0: \mu_{\text{Control}} = \mu_{\text{Drug}} \) .

• Alternative Hypothesis (H₁): The drug has an effect, meaning there’s a difference between the average results of the Control and Drug groups: \( H_1: \mu_{\text{Control}} \neq \mu_{\text{Drug}} \) .

t-Test Formula:

For two independent samples, the t-test formula is:

\( t = \frac{ \bar{X}_{\text{Control}} - \bar{X}_{\text{Drug}} }{ \sqrt{ \frac{ s_{\text{Control}}^2 }{ n_{\text{Control}} } + \frac{ s_{\text{Drug}}^2 }{ n_{\text{Drug}} } } } \)

Where:

• \( \bar{X}_{\text{Control}} \) is the mean of the Control group.

• \( \bar{X}_{\text{Drug}} \) is the mean of the Drug group.

• \( s_{\text{Control}}^2 \) is the variance of the Control group.

• \( s_{\text{Drug}}^2 \) is the variance of the Drug group.

• \( n_{\text{Control}} \) is the number of observations in the Control group.

• \( n_{\text{Drug}} \) is the number of observations in the Drug group.

---

Excel t-Test Formula

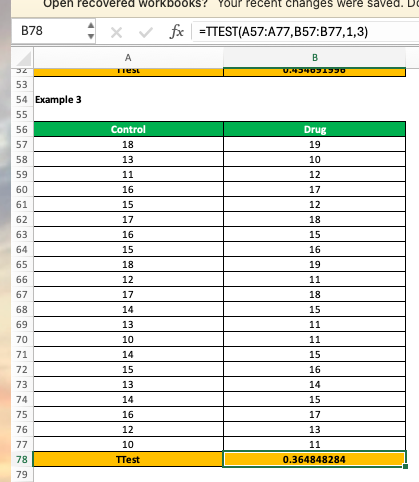
Type this in Excel to compare the groups:

=T.TEST(A7:A26, B7:B26, 2, 3)

• 2 = We’re checking for any difference (two-tailed).

• 3 = Two samples with possibly different variances.

Quick Result

• If p ≤ 0.05: The drug likely has an effect.

• If p > 0.05: No real effect; any difference is probably random.

Your Result: The p-value is 0.3648, which is greater than 0.05. So, no strong proof the drug works—any difference seems random.

If your Excel file has multiple tables on a single sheet, you can use pandas to select specific ranges of cells by row numbers. Here’s how you can target only the table with the "Control" and "Drug" data (located further down on the sheet).

from scipy.stats import ttest_ind

# Example data for Control and Drug groups
control = [18, 13, 11, 16, 15, 17, 16, 15, 18, 17, 14, 13, 10, 14, 15, 13, 16, 12, 10]
drug = [19, 10, 12, 17, 12, 18, 15, 16, 11, 18, 15, 11, 11, 15, 14, 17, 13, 11, 11]

# Perform two-sample t-test with unequal variance
t_stat, p_value = ttest_ind(control, drug, equal_var=False)

# Print the p-value
print("p-value:", p_value)

Steps to Read a Specific Table in Excel

1. Load the Excel sheet into a DataFrame.

2. Select only the rows that contain the "Control" and "Drug" data (from row 57 onward, in this example).

3. Perform the t-test on the selected data.

Python Code Example

import pandas as pd
from scipy.stats import ttest_ind

# Replace with the actual path to your Excel file
file_path = 'path_to_your_file.xlsx'

# Load the entire sheet (assuming the data is on one sheet)
sheet_data = pd.read_excel(file_path, sheet_name='Sheet1')  # Update 'Sheet1' with the actual sheet name

# Select the specific rows for the Control and Drug table (e.g., rows 56 to 76 in zero-indexing)
control_drug_data = sheet_data.loc[56:75, ['Control', 'Drug']].dropna()

# Extract Control and Drug columns as separate arrays
control = control_drug_data['Control']
drug = control_drug_data['Drug']

# Perform two-sample t-test with unequal variance
t_stat, p_value = ttest_ind(control, drug, equal_var=False)

# Display the t-statistic and p-value
print("t-statistic:", t_stat)
print("p-value:", p_value)

Explanation of Code

• sheet_name: Update this to the name of the sheet containing the tables.

• loc[56:75, ['Control', 'Drug']]: This selects rows 57 to 76 (because indexing starts at 0) and only the columns "Control" and "Drug". Adjust these row numbers based on your table location.

• dropna(): Removes any empty cells, ensuring clean data for the t-test.

• ttest_ind: Performs the two-sample t-test.

Expected Output

If the code runs successfully, you’ll get the t-statistic and p-value:

t-statistic: <calculated_value>
p-value: <calculated_value>

Quick Interpretation

• If p-value ≤ 0.05: Significant difference between Control and Drug groups.

• If p-value > 0.05: No significant difference; any observed difference might be random.

This approach lets you focus on a specific part of the sheet, which is useful when dealing with multiple tables on the same sheet. Adjust the row numbers if your table is in a different location. Let me know if you need further assistance!

A/B test case

• Old Ad Clicks: Simulated to have an average around 30 clicks with some variation (standard deviation of 5).

• New Ad Clicks: Simulated to have an average around 35 clicks, slightly higher than the old ad, with similar variation (standard deviation of 5).

Example Data (First 5 Clicks)

• Old Ad Clicks: [32.48, 29.31, 33.24, 37.62, 28.83]

• New Ad Clicks: [36.62, 33.07, 31.62, 38.06, 40.15]

T-Test Results

• t-statistic: -6.87

• p-value: 5.97×10−105.97 \times 10^{-10}5.97×10−10 (essentially zero)

Interpretation

Since the p-value is much smaller than 0.05, we can conclude there’s a statistically significant difference between the clicks on the old and new ads. The new ad likely generates more clicks on average, suggesting it’s more effective than the old one.