Regressão Linear em Python

Neste artigo, vamos aprender um pouco sobre regressão linear em Python, explorando conceitos básicos e desvendando códigos que te levarão entender essa ferramenta. Estes conhecimento pode abrir portas para a análise de dados e a construção de modelos preditivos eficazes.

Começando com um modelo super simples, onde utilizaremos a função numpy.polyfit do Python, esta função está na biblioteca Numpy.

#Entrada de dados experimentais, valores de x e y, importando o pacote numpy
import numpy as np
x = np.array([0, 1., 2., 3, 4, 5, 6])
y = np.array([0, 2.2, 4.1, 6.7, 8.0, 9.8, 13])
mod_linear = np.polyfit(x, y, 1) #valores de x, valores de y e a ordem do polinômio

# y = a * x + b
a = float(mod_linear[0])
b = float(mod_linear[1])

O numpy.polyfit encontra a melhor curva que se ajusta a um conjunto de pontos, é uma função que utiliza o método dos mínimos quadrados para encontrar os coeficientes de um polinômio, minimizando a diferença entre os pontos e a curva gerada. O usuário que escolhe qual será a ordem do polinômio. Neste caso usaremos uma reta, então grau 1.

y_mod = a * x + b

#importando o pacote matplotlib para a construção do gráfico
import matplotlib.pyplot as plt
plt.plot(x,y, "o", label = "pontos experimentais")
plt.plot(x,y_mod, "-r", label = "modelo")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Ajuste de uma reta")
plt.legend()
plt.show()

print(f"Coeficiente angular: {a:6.4f}")
print(f"Coeficiente linear: {b:6.4f}")

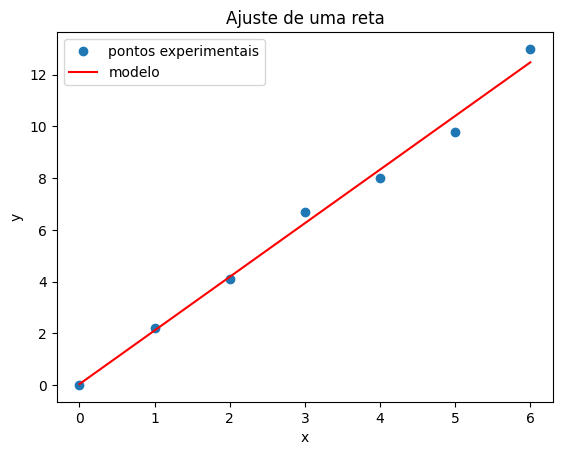
Neste exemplo o coeficiente angular resultou no valor 2,075 e o coeficiente linear no valor 0,032.

O coeficiente de determinação, geralmente representado por R², é uma medida estatística fundamental que indica a qualidade do ajuste de um modelo de regressão linear a um conjunto de dados. Em termos mais simples, ele revela o quão bem a linha de regressão (ou curva, em casos de polinômios) representa a relação entre as variáveis.

#Calculando o coeficiente de determinação do ajuste
yresid = y - y_mod
SQresid = sum(yresid**2)
y_tot = y - np.mean(y)
SQtotal = sum(y_tot**2)
R2 = 1 - SQresid/SQtotal
print('O coeficiente de determinação do ajuste é {:.4f}'.format(R2))

Existem outras bibliotecas e funções que realizam a mesma tarefa, por exemplo linergress da biblioteca Scipy, porém esta já apresenta o coeficiente de determinação estimado.

import numpy as np
x = np.array([0, 1., 2., 3, 4, 5, 6])
y = np.array([0, 2.2, 4.1, 6.7, 8.0, 9.8, 13])

from scipy import stats

a, b, r, p_value, std_err = stats.linregress(x, y)

y_mod = a * x + b

import matplotlib.pyplot as plt
plt.plot(x,y, "o", label = "pontos experimentais")
plt.plot(x,y_mod, "-r", label = "modelo")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Ajuste de uma reta")
plt.legend()
plt.show()

print(f"Coeficiente angular: {a:6.3f}")
print(f"Coeficiente linear: {b:6.3f}")
print(f"Coeficiente de determinação: {r**2:6.4f}")

Espero ter ajudado um pouco na compreensão da regressão linear.

Até a próxima.