Generative Adversarial Networks (GANs) have garnered significant attention in the field of Artificial Intelligence, not just for their innovative methods in generating and enhancing data, but also for their fundamental role in applications such as creating photorealistic images, transforming styles in pictures, and generating realistic human faces among others. First unveiled by Ian Goodfellow and his team in a 2014 NeurIPS paper, GANs stand out as machine learning systems adept at replicating specific data distributions. At their core, they consist of two interlinked neural networks: the generator, responsible for creating data, and the discriminator, whose task is to differentiate between genuine and simulated data. This interplay results in a unique training process, with GANs operating in an “adversarial” manner, formulated as a supervised learning challenge. Here, the generator aspires to craft data so genuine that the discriminator is deceived approximately 50% of the time.

One notable advancement within GANs is the emergence of Deep Convolutional GANs (DC-GANs), which utilize convolutional layers and have proven especially effective in generating high-quality, realistic images for a myriad of applications. These networks have been very important in various achievements in image and video generation. Renowned applications include the transformation of image aesthetics via CycleGAN and the synthesis of hyper-realistic human faces using StyleGAN, as exemplified on the “This Person Does Not Exist” platform.

Architecture

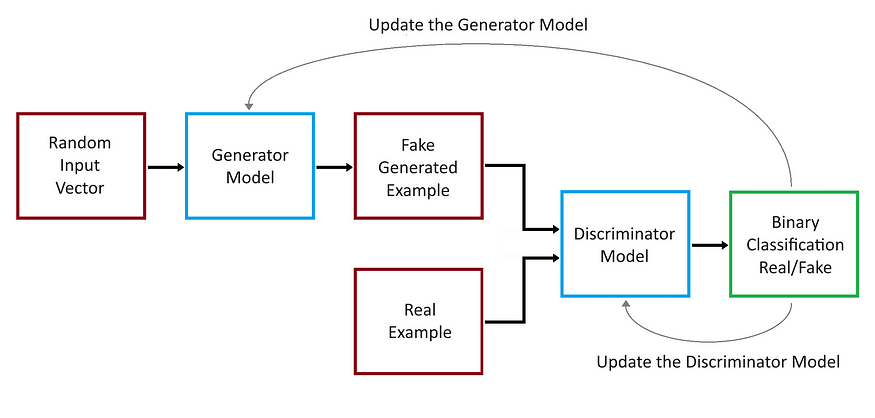
Image by the author

A Generative Adversarial Network (GAN) consists of two neural networks, namely the Generator and the Discriminator, which are trained simultaneously through adversarial training.

1. Generator: This network takes random noise as input and produces data (like images). Its goal is to generate data that’s as close as possible to real data.

2. Discriminator: This network takes real data and the data generated by the Generator as input and attempts to distinguish between the two. It outputs the probability that the given data is real.

During training, the Generator tries to produce data that the Discriminator can’t distinguish from real data, while the Discriminator tries to get better at differentiating real data from fake data. The two networks are in essence competing in a game: the Generator aims to produce convincing fake data, and the Discriminator aims to tell real from fake. This adversarial process leads to the Generator creating increasingly better data over time.

GAN Model Training

During training, GAN takes in two inputs, random noise data and an input data that is not labelled. Using these two inputs, it generates data that resembles the input data. Since all the inputs to the GAN are unlabeled, GAN is a type of unsupervised machine learning.

Internally GAN has two neural networks that compete with each other. The goal of the generator network is to deceive the discriminator network and the goal of the discriminator network is to correctly identify if the input is real or fake.

Generator

The generator’s primary role is to generate data. Initially, this data is likely to be random noise because the generator starts without much knowledge about the true data distribution. Over time, as the GAN is trained, the generator learns to produce data that approximates the real data distribution.

Input: The generator takes in a random noise vector, usually sampled from a normal or uniform distribution. This vector serves as a seed or starting point for data generation.

Architecture: While the architecture can vary, generators in many popular GANs (like DCGAN) are built using transposed convolutional layers (often called “deconvolutional” layers, though that’s a misnomer), which help in upsample the noise vector to produce an image. The generator usually consists in the sequence of the following components.

• Input Layer: The generator starts with an input layer that takes in a random noise vector, usually sampled from a normal or uniform distribution.

• Fully Connected Layers: Early in the network, fully connected layers may be used to transform the input noise vector into a suitable shape for further processing.

• Batch Normalization: This technique is often used between layers to stabilize learning by normalizing the output of a previous layer. It helps in addressing issues like mode collapse and aids in faster convergence.

• Activation Functions: ReLU (Rectified Linear Unit) or Leaky ReLU are common choices for activation functions in the generator. These functions introduce non-linearity to the model, enabling it to generate complex data.

• Transposed Convolutional Layers: Also known as deconvolutional layers (though technically a misnomer), these layers are fundamental in the generator. They upsample the input from the previous layer to a higher spatial dimension, effectively doing the opposite of what convolutional layers do in a CNN.

• Reshaping Layers: These layers are used to reshape the data into the desired output format, especially when generating images.

• Output Layer: The final layer usually employs a tanh or sigmoid activation function, depending on the nature of the data being generated. For image generation, a tanh function is often used to output pixel values in a normalized range.

• Training: During training, the generator continuously learns to produce data that the discriminator can’t distinguish from real data. The generator updates its weights based on feedback from the discriminator, refining its ability to create convincing fake data.

Output: The generator produces data as its output. In the case of a GAN designed for image generation, the output would be an image. The data is then passed to the discriminator to be classified as real or fake.

Training: During training, the generator tries to deceive the discriminator by producing data that the discriminator can’t distinguish from real data.
The generator updates its weights based on feedback from the discriminator. If the discriminator correctly identifies the generated data as fake, the generator adjusts its weights to produce more convincing data during the next iteration.
The process is a kind of “game” where the generator constantly tries to improve, aiming to eventually produce data that’s nearly indistinguishable from real data.

Challenges: :

• Mode Collapse: This is a situation where the generator produces a limited variety of outputs, even if trained on diverse data. It’s like the generator figuring out one particular “type” of fake data that the discriminator struggles with and then producing only that kind of data. It can be mitigated by introducing regularization techniques, and diversity-promoting loss functions, or using different training methodologies like minibatch discrimination.

• Training Instability: GANs, in general, are notorious for being difficult to train, with the generator’s training being particularly challenging. This is because the optimization landscape involves two models (generator and discriminator) that are being trained simultaneously in a dynamic setting. This problem can be reduced by adopting employ techniques such as Gradient Penalty, using learning rate schedulers, or adopting more specific GAN architectures that are more stable for the given problem.

Discriminator

The discriminator’s role is to distinguish between real and fake data. If you’re thinking about GANs in the context of images (which is a common application), the discriminator tries to tell apart real images from the fake images generated by the generator.

Input: Receives data samples, which can be either real data or generated data.

Output: Provides a scalar value between 0 and 1, representing the probability that the input sample is real. A value close to 1 suggests the sample is likely real, while a value close to 0 suggests it’s likely fake.
The actual architecture (like the number of layers, type of layers, etc.) can vary widely based on the specific problem and dataset. For image data, discriminators often use convolutional neural networks (CNNs).

Architecture: The architecture of the discriminator often mirrors that of traditional convolutional neural networks (CNNs), but with some adjustments. It usually consists in the sequence of the following components.

• Convolutional Layers: These layers are fundamental in processing image data. They help in extracting features from the input images. The number of convolutional layers can vary depending on the complexity of the data.

• Batch Normalization: This is sometimes used between layers to stabilize learning by normalizing the input to a layer.

• Activation Functions: Leaky ReLU is a common choice for activation functions in the discriminator. It allows a small gradient when the unit is not active, which can help maintain the gradient flow during training.

• Pooling Layers: Some architectures use pooling layers (like max pooling) to reduce the spatial dimensions of the input data progressively.

• Fully Connected Layers: At the end of the network, fully connected layers are used to process the features extracted by the convolutional layers, culminating in a final output layer.

• Output Layer: The final layer is typically a single neuron with a sigmoid activation function to output a probability value.

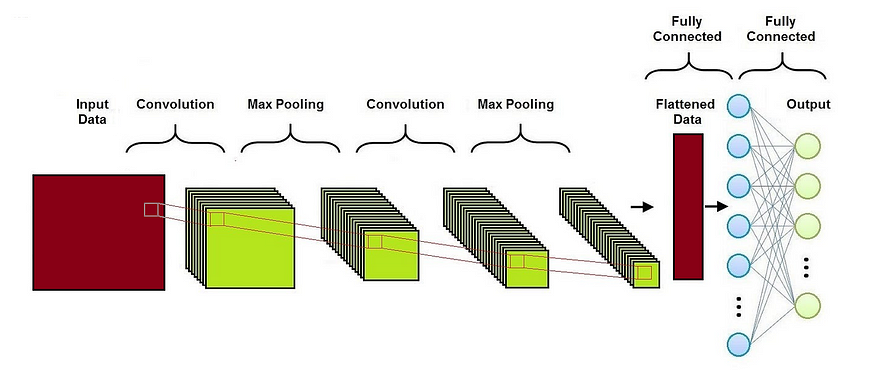
Image by the author

Obviously, the actual can vary widely based on the specific problem and dataset. The main difference between a classical CNN architecture and a GAN discriminator architecture are the following:

• Loss Function: CNNs use many different loss functions, while GAN’s Discriminator always uses binary cross-entropy loss since it’s distinguishing between two classes (real vs. fake).

• Feedback Loop: While in CNN there’s no feedback loop with another network during its training and the CNN is trained in isolation using a labeled dataset, GAN’s Discriminator operates in tandem with the Generator. The Discriminator provides feedback to the Generator, allowing it to improve its image generation capabilities.

• Output Activation Function: Depending on the task, CNNs might use or not softmax activation, while GAN’s Discriminator typically uses a sigmoid activation function in the output layer to provide a probability score indicating whether the image is real or fake.

• Depth and Complexity: GAN’s Discriminator is often simpler and shallower than conventional CNNs, but of course the complexity depends on the specific GAN architecture and the dataset being used.

Training: During training, the discriminator updates its weights in the following way.

It is shown real data and should be trained to output values close to 1. It is shown fake data (generated by the generator) and should be trained to output values close to 0.

Challenges: :

• Overpowering Discriminator: If the discriminator becomes too strong too quickly, it might always give a very confident output (either close to 0 or 1) for any input, making it hard for the generator to learn. This issue can be mitigated by implementing techniques like label smoothing, feature matching, or deliberately slowing down the training of the discriminator.

• Weak Discriminator: On the other hand, if the discriminator is too weak, the generator might not get meaningful feedback to improve. The balance between the generator and discriminator during training is crucial for the success of a GAN. This problem can be reduced by enhancing the capacity of the discriminator, carefully tuning its learning rate, or using advanced architectures that improve discriminative power.

GAN Loss

Generative Adversarial Networks (GANs) utilize loss functions to train both the generator and the discriminator. The loss function helps adjust the weights of these models during training to optimize their performance. Both the generator and the discriminator use the binary cross-entropy loss to train the models, that can be written as

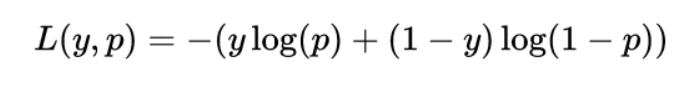
where:

• L(y,p) is the loss value;

• y is the true label (either 0 or 1);

• p is the predicted probability of the sample belonging to class 1.

Discriminator Loss

The discriminator’s goal is to correctly classify real samples as real and fake samples (produced by the generator) as fake. Its loss is typically represented as:

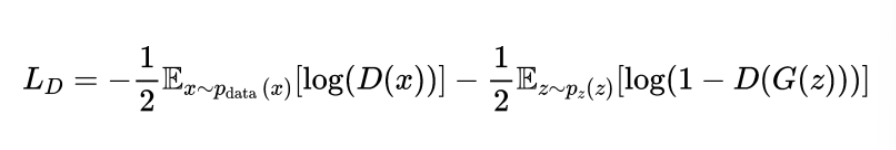
where

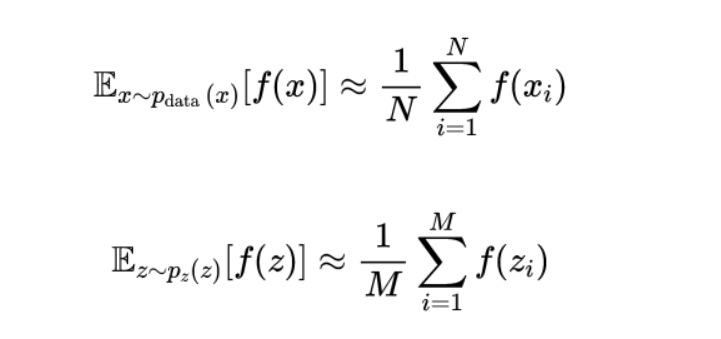
x_i​ are samples from the real dataset, N is the number of samples from the real dataset, z_i​ are samples from the noise distribution, and M is the number of samples from the noise distribution.

The first term on the right hand penalizes the discriminator for misclassifying real data, while the second term penalizes the discriminator for misclassifying the fake data produced by the generator.

Generator Loss

The generator’s goal is to produce samples that the discriminator incorrectly classifies as real. Its loss is typically represented as:

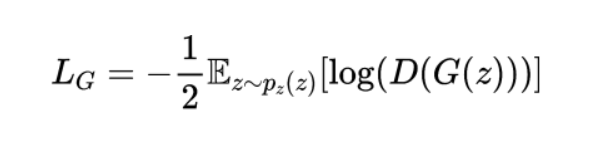
This term penalizes the generator when the discriminator correctly identifies its outputs as fake.

Combined Loss

The combined GAN Loss, often referred to as the minimax loss, is a combination of the discriminator and generator losses. It can be expressed as:

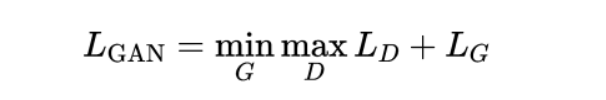
This represents the adversarial nature of GAN training, where the generator and the discriminator are in a two-player minimax game. The discriminator tries to maximize its ability to classify real and fake data correctly, while the generator tries to minimize the discriminator’s ability by generating realistic data.

Gradient Penalties

Gradient penalty is a technique used to stabilize the training by penalizing the gradients if they become too steep. This can help in stabilizing the training and avoiding issues like mode collapse.

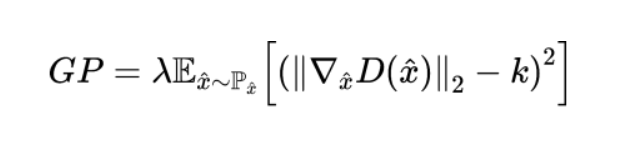
where

• GP represents the gradient penalty term;

• λ is a hyperparameter that controls the strength of the penalty;

• the gradient component is the gradient of the discriminator’s output with respect to its input x^;

• P_x^​ represents the distribution of interpolated samples between real and generated data;

• k is a target norm for the gradient, often set to 1;

The discriminator loss with gradient penalty can be incorporated as follows:

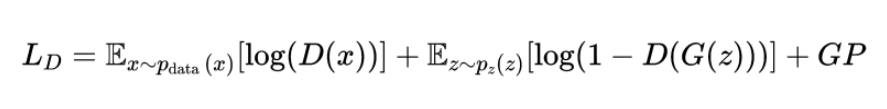
This loss function consists of the usual GAN discriminator loss components for real and generated data, plus the gradient penalty term to regularize the discriminator’s behavior. The key concept is that by penalizing large gradients, you encourage the discriminator to behave more smoothly, which can lead to a more stable training process for both the generator and the discriminator. This approach can be adjusted and adapted depending on the specific characteristics of the GAN architecture and the problem at hand.

Implementation

The following simple code implements a DC-GAN architecture with a generator and discriminator to generate fake images resembling the MNIST dataset digits. The generator learns to create realistic-looking images, while the discriminator learns to distinguish between real and fake images. During training, both the generator and discriminator networks are updated iteratively in a minimax game until the generator produces convincing images. After the code you can find a short description of all the components.

import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.layers import (Dense, Flatten, Reshape,
                                     Conv2D, Conv2DTranspose, LeakyReLU, BatchNormalization)
from tensorflow.keras.datasets import mnist
import matplotlib.pyplot as plt


# Generator
def make_generator_model():
    model = keras.Sequential()

    # Foundation for 7x7 image
    model.add(Dense(7 * 7 * 256, activation='relu', input_shape=(NOISE_DIM,)))
    model.add(Reshape((7, 7, 256)))

    # Upsample to 14x14
    model.add(Conv2DTranspose(128, (5, 5), strides=(1, 1), padding='same', activation='relu'))
    model.add(BatchNormalization())

    # Upsample to 28x28
    model.add(Conv2DTranspose(64, (5, 5), strides=(2, 2), padding='same', activation='relu'))
    model.add(BatchNormalization())

    model.add(Conv2DTranspose(1, (5, 5), strides=(2, 2), padding='same',
                              activation='tanh'))  # Single channel for grayscale MNIST images

    return model


# Discriminator
def make_discriminator_model():
    model = keras.Sequential()
    model.add(Conv2D(64, (5, 5), strides=(2, 2), padding='same', input_shape=[28, 28, 1]))
    model.add(LeakyReLU())
    model.add(BatchNormalization())

    model.add(Conv2D(128, (5, 5), strides=(2, 2), padding='same'))
    model.add(LeakyReLU())
    model.add(BatchNormalization())

    model.add(Flatten())
    model.add(Dense(1))  # No activation here since we use from_logits=True in the loss

    return model


def discriminator_loss(real_output, fake_output):
    real_loss = cross_entropy(tf.ones_like(real_output), real_output)
    fake_loss = cross_entropy(tf.zeros_like(fake_output), fake_output)
    total_loss = real_loss + fake_loss
    return total_loss

def generator_loss(fake_output):
    return cross_entropy(tf.ones_like(fake_output), fake_output)

# Training loop
def train_step(images):
    noise = tf.random.normal([BATCH_SIZE, NOISE_DIM])

    with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
        generated_images = generator(noise, training=True)

        real_output = discriminator(images, training=True)
        fake_output = discriminator(generated_images, training=True)

        gen_loss = generator_loss(fake_output)
        disc_loss = discriminator_loss(real_output, fake_output)

    gradients_of_generator = gen_tape.gradient(gen_loss, generator.trainable_variables)
    gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables)

    generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))
    discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))

def train(dataset, epochs):
    for epoch in range(epochs):
        for image_batch in dataset:
            train_step(image_batch)

# Generate and save images
def generate_and_save_images(model, epoch, test_input):
    predictions = model(test_input, training=False)
    predictions = tf.reshape(predictions, (-1, 28, 28))  # Reshape to [batch_size, 28, 28]

    fig = plt.figure(figsize=(4, 4))

    for i in range(predictions.shape[0]):
        plt.subplot(4, 4, i + 1)
        plt.imshow(predictions[i] * 127.5 + 127.5, cmap='gray')
        plt.axis('off')

    plt.savefig(f'image_at_epoch_{epoch:04d}.png')
    plt.show()


# Test the GAN model
if __name__ == "__main__":
    # Load the dataset
    (train_images, train_labels), (_, _) = mnist.load_data()
    train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')
    train_images = (train_images - 127.5) / 127.5  # Normalize the images to [-1, 1]

    # Hyperparameters
    BUFFER_SIZE = 60000
    BATCH_SIZE = 256
    NOISE_DIM = 100

    generator = make_generator_model()
    discriminator = make_discriminator_model()

    # Define the loss and optimizers
    cross_entropy = tf.keras.losses.BinaryCrossentropy(from_logits=True)

    generator_optimizer = tf.keras.optimizers.Adam(1e-4)
    discriminator_optimizer = tf.keras.optimizers.Adam(1e-4)

    # Batch and shuffle the data
    train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(BUFFER_SIZE).batch(BATCH_SIZE)

    EPOCHS = 50

    # Train the GAN
    train(train_dataset, EPOCHS)

    # Generate some test noise samples
    test_input = tf.random.normal([16, NOISE_DIM])
    generate_and_save_images(generator, EPOCHS, test_input)

• Generator: The generator model consists of a series of dense layers and transposed convolutional layers (also known as deconvolutional layers). It starts with a dense layer that reshapes the noise input into a 7x7 image with 256 channels. It then upsamples this image using two transposed convolutional layers until it reaches the size of 28x28, which is the size of the MNIST images.Batch normalization is applied after the upsampling layers to stabilize training. The final layer outputs a single channel image (grayscale) with pixel values between -1 and 1 due to the ‘tanh’ activation function.

• Discriminator: The discriminator model consists of convolutional layers followed by dense layers. It processes the input images and gradually down-samples them using convolutional layers with LeakyReLU activations and batch normalization. The output is a single scalar representing the model’s belief that the input is a real image (larger value) or a fake one (smaller value).

• Loss Functions:discriminator_loss penalizes the discriminator for misclassifying real images and for being fooled by the generator, while generator_losspenalizes the generator if the discriminator can easily tell its images are fake.

• Training Loop (train_step function): Random noise is generated and passed through the generator to produce fake images. The discriminator then evaluates both real images and the fake images generated by the generator. Gradients are computed for both the generator and discriminator based on their losses, and their parameters are updated using the Adam optimizer.

• Main Training Loop (train function): The train_step function is called for each batch of real images in the dataset, for a specified number of epochs.

• Image Generation and Visualization (generate_and_save_images function): This function takes the current generator model, generates images from random noise, reshapes and scales them to visual range, and then saves and displays them using Matplotlib.

Applications

Generative Adversarial Networks (GANs) have gained significant attention since their inception and have been employed in a wide range of applications. Some of the most prominent applications include:

Image Generation: This was one of the initial applications of GANs. They can be trained to generate high-resolution, realistic images from random noise.

Data Augmentation: In domains where data is limited, GANs can be used to augment the dataset by generating new samples, which can be particularly valuable for training more robust machine learning models.

Style Transfer: GANs can modify the style of images, such as converting photos into the style of famous paintings or changing day scenes to night scenes.

Super-Resolution: Super-resolution GANs (SRGANs) can enhance the resolution of images, turning low-res images into high-res counterparts.

Image-to-Image Translation: GANs can be used to translate images from one domain to another, such as turning satellite images into maps or sketches into colored images.

Generating Art: Artists and hobbyists have used GANs to create original pieces of art, both in the form of static images and videos.

Conclusion

In conclusion, Generative Adversarial Networks (GANs) represent a transformative step forward in the domain of Artificial Intelligence and machine learning. Their unique architecture, which pits a generator against a discriminator in an intricate dance of data creation and validation, has opened up avenues for innovation previously deemed challenging. From crafting photorealistic images to pioneering advancements in data augmentation, GANs have firmly established their significance in today’s AI landscape. While they come with their own set of challenges and complexities, the continuous research and advancements in this field provide a promising glimpse into the future.