Recursion is a fundamental concept in programming that allows functions to call themselves to solve problems in a repetitive yet elegant way. In this blog, we'll break down what recursion is, how it works, and see practical examples that illustrate its beauty and power. This is the first in a series of articles on recursion, so stay tuned for more advanced topics to come!

What is Recursion?

Recursion is a technique where a function calls itself in its code to break down a task into simpler, repeatable steps. In other words, rather than using loops to repeat code, recursion allows a function to handle these repetitions by calling itself with adjusted parameters each time.

Let’s start by understanding how functions work without recursion and then see how recursion can simplify repetitive tasks.

1. Breaking Down Function Calls Without Recursion

Consider this example:

static void number1 (int n){
    System.out.println(n);
    number2(2);
}

static void number2(int n) {
    System.out.println(n);
    number3(3);
}

static void number3 (int n){
    System.out.println(n);
}

In this code:

The main function calls number1.
number1 prints its argument n and then calls number2, which prints 2.
Finally, number2 calls number3, which prints 3.

Notice one thing, each function is doing almost the same thing with slight changes, but we've had to write separate functions for each task. This is where recursion shines. Instead of writing multiple functions for similar tasks, we can create a single function that calls itself, making the code shorter, cleaner, and easier to manage.

Using recursion, we can simplify the code above. Here’s how:

static void number (int n){
    if (n>3){
        return;
    }
    System.out.println(n);
    number(n+1);
}

How it Works:

This function number calls itself with n + 1 each time until n exceeds 3.
The line if (n > 3) { return; } is the base condition. It prevents the function from running indefinitely by stopping the recursion when n reaches a certain point.

In this recursive version:

The base condition (if (n > 3)) stops the recursive calls after the third print.
We achieve the same output as before with just one function instead of three.

2. Calculating Factorial with Recursion

Let’s move to a classic example—calculating the factorial of a number using recursion.

Factorial Concept:

Factorial of num (written as num!) is the product of all positive integers from num down to 1.
For example, 5! = 5 * 4 * 3 * 2 * 1 = 120.
We need a base condition to stop recursion. Here, num == 0 is a natural stopping point since 0! = 1.

Here’s how we could write this function recursively:

static void getFact (int num , int fact){
    if (num==0){
        System.out.println(fact);
        return;
    }
    fact = fact*num;
    getFact(num-1,fact);
}

Explanation:

The getFact function reduces num by 1 on each call, multiplying fact by num until num reaches 0.
When num == 0, the function stops, printing the result of fact.

Important: Always ensure you have a base condition in recursive functions, or the function will keep calling itself indefinitely, potentially crashing your program.

3. Fibonacci Sequence with Recursion

Another powerful use of recursion is in generating the Fibonacci sequence. In the Fibonacci sequence, each number is the sum of the two preceding ones. Here’s what it looks like :

Fibonacci Series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

How it Works:

The series starts with 0 and 1.
Every subsequent number is the sum of the previous two: f(n) = f(n-1) + f(n-2)

To calculate the nth Fibonacci number using recursion:

static int fbs(int n){

    if (n<2){
        return n;
    }
    return fbs(n-1) + fbs (n-2);
}

Explanation:

The base condition here is if (n < 2), as f(0) and f(1) are the start of the sequence and do not require further calculations.
For any n greater than 1, the function calls itself with fbs(n - 1) and fbs(n - 2).

Visualizing Recursion: Here’s where recursion gets interesting. When you call fbs(4), for instance, the function will split into multiple calls to calculate fbs(3) and fbs(2), which themselves split further. This process continues until the base condition is met for all branches. Check out the recursion tree I’ve included to see how each call stacks and resolves.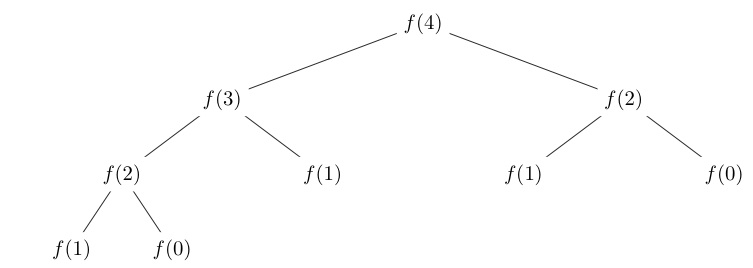

Recursion Tips & Common Pitfalls

Use a Base Condition: Every recursive function must have a clear base condition to prevent infinite recursion. This is a crucial rule in recursion.
Check Edge Cases: When dealing with recursion, think about edge cases, like passing a negative number or an extremely large number.
Mind the Stack Overflow: Recursive calls add to the call stack, which is limited. Too many recursive calls can lead to a StackOverflowError.
Debugging Helps: To understand the flow of a recursive function, I used debugging tools to step through each call in IntelliJ IDE.

GitHub Repository

I've added this code and more recursive challenges in my GitHub repository. Feel free to check it out, fork the repo, and try running and modifying the code yourself!

My GitHub Repository

LeetCode Problems

I’ll cover popular LeetCode recursion problems in the final post of this series, where we’ll apply recursion to real-world coding challenges. Stay tuned!

Wrapping Up

Recursion allows us to break down complex problems into smaller, repeatable tasks. It’s especially useful for tasks like calculating factorials, traversing data structures, and generating sequences. Remember:

Always define a base condition.
Practice makes perfect! Recursion can be tricky at first, but I practiced it.

In the next article, we’ll go deeper into recursion, exploring concepts like tail recursion, backtracking, and optimizing recursive solutions.

Recursion in Java: Part 1

Table of contents