Big O notations
 Atuhaire Collins Benda
Atuhaire Collins Benda
Have you ever poured your heart and soul into writing what you believed to be the pinnacle of code excellence, only to have your confidence shattered by your colleague having much better code? Then, during the code review, the senior trashes you and your colleague's code in favor of a much more straightforward and effortlessly effective one. Hmmm, so how do I determine whether my code is great or subpar? Imagine having a system or metric to categorize how shaky my code is, similar to how earthquakes are quantified or contrasted with the Richter scale. Something that could classify the 'shittiness' of my code and provide a standardized measure of its quality?
In our pursuit of an objective measure of code quality, I encountered the term "Big O Notation." It initially seemed a bit abstract and theoretical, but its importance cannot be overstated. Big O Notation provides a systematic and universally accepted way to measure and compare the efficiency of algorithms. It's like a compass that guides you toward writing code that not only works but works efficiently, even when faced with vast amounts of data.
So why should you care about Big O notation? Let me break it down for you in a way that'll make you want to high-five your computer screen!
Time-Saving : Imagine you're at a big tech company tasked you with writing an algorithm. Knowing Big O helps you create algorithms that work faster and more efficiently. Picture this: you shave off a whole hour of processing time! That's like gaining an extra episode in your Netflix binge-watching marathon. Who doesn't want that?
Code Lingo: Big O gives you a secret language to chat about code performance with your team members. No more vague "it's kinda slow" talk. You'll be tossing around phrases like O(1), O(log n), and O(n^2) like a coding maestro. It's like having a secret handshake in the world of devs.
Trade-off Tango: Sometimes we face tough decisions while we code. Should I go for the flashy, super-speedy code that gobbles up memory like a hungry hippo, or opt for the lean, memory-efficient one that takes a bit longer to finish? Big O helps you weigh these choices with confidence. It's like picking between a turbocharged sports car and a fuel-efficient hybrid but for your code. And most of all helps me understand the different things I can factor into my decisions
Code CSI: Ever had a piece of code go rogue, slowing down your app or causing it to crash? Big O is your trusty detective tool. It helps you spot the misbehaving culprits in your code lineup. Think of it as your code CSI kit, ready to uncover performance bottlenecks faster than Sherlock Holmes or Jake Peralta.
Interview Hero: Job interviews in tech often throw Big O questions your way. Think of it as your secret weapon. Nail those questions, and you're one step closer to landing your dream job in a swanky tech company. It's like having a cheat code for leveling up in the world of coding careers.
Let's Talk Timing: What Makes Code "Better"?
When we say we want "better" code, what exactly do we mean? Is it all about speed, making our code run faster than Usain Bolt? Or perhaps it's about being more frugal with memory, like a financial guru managing their budget. And let's not forget about readability – the art of crafting code that's as clear as a crystal-clear mountain stream.
But here's where things get a bit tricky. If we use time as our sole metric for measuring code quality, we run into a snag. Time can be a slippery character, measured differently depending on various factors like the computer's processing power, the phase of the moon (okay, maybe not that last one).
For instance, think about rendering a high-definition image. On your speedy gaming rig, it might take a mere blink of an eye, but on Aunt Mildred's vintage computer, it could feel like an eternity. So, if we rely solely on time measurements, we might miss the bigger picture.
Enter the World of Operations
So, if not time, then what? Well, here's where we bring some math into the mix (don't worry, it's not rocket science). Instead of counting seconds, let's count something that remains constant no matter what computer you're on – the number of simple operations the computer has to perform.
But hold on, what's an operation, you ask? Great question!
An operation is a fundamental action the computer performs. These can be as simple as adding two numbers, comparing values, or moving data around in memory. The beauty of operations is that they're like LEGO blocks – you can use them to build complex structures, and the number of operations needed to perform a task remains consistent across different machines.
For example, let's say you're sorting a list of names alphabetically. Each time you compare two names to decide which one comes first, that's an operation. If you have a list of 10 names, you might need a handful of operations. If you have a list of 10,000 names, you'll need a lot more operations. if 'n' here represents the number of items you need to sort then increasing n increases the number of operations.
So, when we talk about better code, we're often talking about code that does the same task with fewer operations. In other words, it's like finding the shortest route from point A to point B, where each operation is a step – the fewer steps, the faster you get there! And that, my friends, is the magic of measuring code quality by counting operations. It levels the playing field, allowing us to evaluate code based on its efficiency and performance, regardless of the computer it runs on. 🚀
We'll explore two functions designed to perform the same task: calculating the sum of all numbers from 1 to 'n'. However, these functions take different paths to reach the same destination. One uses a traditional loop, while the other employs a mathematical formula. Our goal is to compare these two approaches based on their operational efficiency, shedding light on how the choice of coding techniques can significantly impact code performance. let's start by taking a closer look at the number of operations in both functions, including the operations within the loop:
Function 1: addUpToSecond
function addUpToSecond(n) {
return n * (n + 1) / 2; // 3 operations (multiplication, addition, division)
}
For addUpToSecond(5), calculates the sum directly using a mathematical formula.
So, for addUpToSecond(5), there are a total of 3 operations(multiplication, addition, and division) regardless of the size of n.
That means that if I pass in 1000 or 100000 it will still take the same number of operations.
Function 2: addUpToFirst
function addUpToFirst(n) {
var total = 0; // 1 operation
for (var i = 0; i <= n; i++) {
total += i; // 4 operations (addition, assignment of i, comparison, increment of i)
}
return total; // 1 operation
}
For addUpToFirst(5), the number of operations is as follows:
Initializing
totalis the first operation and it occurs once when the program is run Now if we enter the loop:We know that
total += i;is shorthand fortotal = total + i;. Meaning there are two operations happening addition and assignment. But notice this is happening in a loop so it is repeatedntimes. So now we havenadditions andnassignments. So ifn=5, the loop will do repeat 5 times so there will be 5 additions and 5 subtractions.Let’s look at the line
for (var i = 0; i <= n; i++)where the loop is createdvar i = 0: operation for assigning 0 toithat happens only once the loop has started.i <= n: Comparison ofiandnwhich happens on every iteration of the loop meaning it occurs n timesi++: This is shorthand fori=i+1which has two operations (addition and assignment) that occur on every iteration. Meaning they happenntimes. (So if n is a billion it happens a billion times)

To get the total number of operations for addUpToFirst(n), we would use 5n+2.but regardless of the exact number the number of operations grows roughly proportionally with n.
The total number of operations for addUpToFirst(5) is (5x5) + 2 = 27 operations.
Now if we compare the two functions:
addUpToFirstforn = 5requires 27 operations.addUpToSecondforn = 5requires 3 operations.
As you can see, addUpToSecond is significantly more efficient in terms of the number of operations, especially as 'n' increases. This emphasizes the efficiency gained by using a mathematical formula instead of a loop, making addUpToSecond it faster and more efficient than addUpToFirst.
Visualizing Code Efficiency: A Closer Look at Execution Time
To get a detailed understanding of how two functions perform in terms of execution time, we'll utilize a helpful tool (https://rithmschool.github.io/function-timer-demo/). However, there's a slight twist here – we'll start with a small 'n' value and gradually increase it to find the optimal results for each function. we'll notice a fascinating trend in the visualization.
Trend 1: Function 1 (addUpToSecond)
For Function 1, which utilizes a loop to calculate the sum, we'll observe the following trend:
Initially, as 'n' starts with a small value (e.g., 10), the execution time is relatively short (measured in microseconds).
However, as we increment 'n' to 100, 1000, and beyond, the execution time steadily increases.
This increase in execution time follows a linear pattern, roughly proportional to 'n'. In the visualization, you'll see a linear slope where execution time gradually rises as 'n' grows.
The key takeaway is that for Function 1, the time it takes to complete the task increases linearly with the size of 'n'. This behavior is consistent with a linear time complexity, often represented as O(n).
Trend 2: Function 2 (addUpToFirst)
For Function 2, which relies on a mathematical formula, we'll observe a different trend:
Similar to Function 1, the execution time starts at a low level when 'n' is small.
However, as 'n' increases, the execution time remains remarkably stable and minimal. It does not exhibit the same linear growth seen in Function 1.
In the visualization, you'll notice a nearly flat line, indicating that the execution time is not significantly affected by changes in 'n'.
This behavior aligns with a constant time complexity, often represented as O(1), where the execution time remains constant, regardless of the input size.
In summary, the trend reveals that Function 1's execution time increases linearly with 'n', while Function 2's execution time remains nearly constant, regardless of the value of 'n'. This visualization vividly illustrates the concept of code efficiency and how the choice of coding techniques can significantly impact the time required to complete a task, especially as the problem size ('n') grows. From this, we can establish that efficiency depends on time and space.
So what is Big 0
Big O notation is a mathematical notation used in computer science and mathematics to describe the upper bound or worst-case scenario of the time complexity or space complexity of an algorithm or function. It provides a way to analyze and compare algorithms based on their efficiency and how they scale with input size. (Think of special notation that helps us describe how fast or slow a computer program is and how it handles bigger and bigger tasks)
In Big O notation, an algorithm's performance is expressed using a function, typically denoted as O(f(n)), where "f(n)" represents the relationship between the input size (often denoted as 'n') and the number of basic operations performed by the algorithm. This function describes how the algorithm's runtime or space usage grows as the input size increases. So f(n) can be linear (f(n) = n), quadratic (f(n) = n^2), constant (f(n) =1), or something entirely different
The most common Big O notations include:
O(1) (Constant Time): The algorithm's runtime or space usage remains constant regardless of the input size. It indicates highly efficient algorithms that execute in a fixed amount of time or require a fixed amount of memory. (This is like having a magic spell that instantly finds the word, no matter how big the book is. It's super fast and always takes the same amount of time, whether it's a small book or a huge library.)
O(log n) (Logarithmic Time): The algorithm's runtime or space usage grows logarithmically with the input size. These algorithms become more efficient as the input size increases. (Think of this as a clever guessing game. As the book gets bigger, you need a few more guesses, but it's still pretty fast, and the more you guess, the faster you get at it.)
O(n) (Linear Time): The algorithm's runtime or space usage scales linearly with the input size. For every additional element in the input, the algorithm performs a constant amount of work. (This is like reading the book page by page. If the book doubles in size, it takes twice as long. It's simple but can get slow for really big books.)
O(n log n) (Logarithmic Time): The algorithm's runtime or space usage grows in proportion to 'n' multiplied by the logarithm of 'n.' Algorithms with this complexity are often efficient and are commonly seen in sorting and searching algorithms. (Imagine reading the book, making some notes, and then finding what you need. It takes a bit longer than just reading but is still pretty efficient.)
O(n^2) (Quadratic Time): The algorithm's runtime or space usage grows quadratically with the input size. It indicates algorithms that perform nested iterations over the input. (This is like checking every word on every page one by one. As the book gets bigger, it takes much more time, and it can be slow for large books.)
O(2^n) (Exponential Time): The algorithm's runtime or space usage grows exponentially with the input size. These algorithms become impractical for large input sizes due to their rapid increase in resource requirements. (This is extremely slow. It's like making a copy of the entire book for every word you want to find. For big books, it's painfully slow)
O(n!) (Factorial Time): The algorithm's runtime or space usage grows factorially with the input size. These algorithms are highly inefficient and are typically used for small, specialized cases. (This is the slowest. It's like writing out every possible combination of words and checking them all. Even for moderately-sized books, it can take forever.)
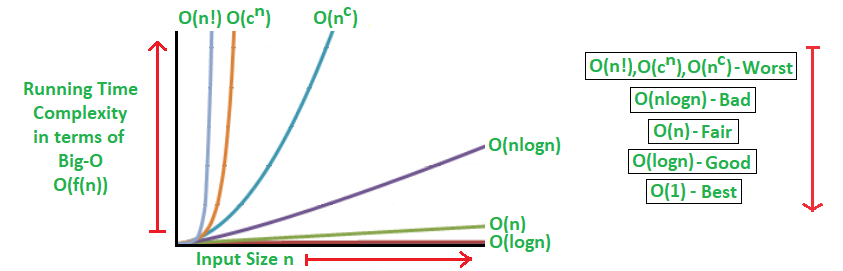
Big O notation provides a standard way to analyze and compare algorithms, enabling developers to make informed decisions about algorithm selection and optimization to ensure efficient and scalable software. It focuses on the worst-case scenario, helping to predict how an algorithm will perform when faced with the largest possible input.
If we go back to the examples discussed earlier
The time complexity of
sumUsingLoopis O(n). This means that as the input size 'n' increases, the number of operations also increases linearly. If 'n' doubles, the number of operations roughly doubles as well.The time complexity of
sumUsingFormulais O(1), which is constant time. Regardless of how large 'n' becomes, the number of operations remains the same. It's highly efficient and doesn't depend on the input size. Contrast:When comparing the two functions, you can see that
sumUsingFormulais far more efficient in terms of time complexity. Its execution time remains constant, making it the preferred choice for large values of 'n.'In contrast,
sumUsingLoophas a linear time complexity. As 'n' grows, the number of operations increases proportionally. This means it might not be the best choice for large datasets or inputs because it can become slower as 'n' gets larger.Big O notation precisely describes this difference in efficiency. It tells us that
sumUsingFormulais O(1), indicating constant time, whilesumUsingLoopis O(n), indicating linear time. So, this allows us to understand and compare the efficiency of algorithms or code. It helps us make informed decisions about which approach to use based on the problem's size and the resources available. In this case, it's clear thatsumUsingFormulais the more efficient option for summing numbers from 1 to 'n' for larger values of 'n.'
Understanding Big O Simplification
You might be wondering how we simplified O(5n + 2) into O(n) .Let's break down how we simplify the Big O notation to O(n).
In Big O notation, we're interested in understanding how the number of operations or the execution time grows concerning the size of the input (usually denoted as 'n'). When simplifying, we focus on the term that has the most significant impact as 'n' becomes large, and we ignore constants and lower-order terms.
In the expression O(5n + 2), we have two terms: 5n and 2.
Here's why we simplify it to O(n):
Focus on the Dominant Term: In this case, the term 5n dominates because its growth rate is directly proportional to 'n.' As 'n' increases, the number of operations increases linearly with 'n' due to the 5n term.
Ignore Constants: Big O notation doesn't concern itself with constants because they don't affect the overall growth rate concerning 'n.' The "+ 2" term represents a constant (2) that doesn't change as 'n' varies.
Ignore Lower-Order Terms: Big O notation focuses on the most significant term that contributes to the growth rate. In this case, 5n is the dominant term, and it's a linear term.
- Arithmetic operations are constant: In most cases, basic arithmetic operations like addition, subtraction, multiplication, and division are considered constant time operations. They take the same amount of time regardless of the values involved.
Variable assignment is constant: Assigning a value to a variable typically takes constant time. It doesn't matter how large or small the value being assigned is; the time it takes remains constant.
Accessing elements in an array (by index) or object (by key) is constant: This statement highlights the concept of constant-time access to elements in data structures like arrays and objects. It doesn't matter how big the array or object is; accessing an element by its index or key takes roughly the same amount of time.
In a loop, the complexity is the length of the loop times the complexity of whatever happens inside the loop: This is a crucial principle in analyzing algorithms with loops. The time complexity of a loop is determined by multiplying the number of iterations (the length of the loop) by the complexity of the operations inside the loop. This helps in understanding how loops impact overall algorithm efficiency.
| Big O Notation | Simplification | Explanation |
| O(2n) | O(n) | Constant factors are dropped; it's still linear growth with 'n'. |
| O(3n^2) | O(n^2) | Constant factors are dropped; it's still quadratic growth with 'n'. |
| O(n + 1000) | O(n) | Constants are dropped; they don't significantly impact growth with 'n'. |
| O(5n^2 + 3n + 1) | O(n^2) | Keep the most dominant term (quadratic); lower-order terms are dropped. |
| O(log n + n) | O(n) | Linear growth (n) dominates logarithmic growth (log n). |
| O(2^log n) | O(2^log n) | No simplification; exponential time complexity remains. |
| O(n^3 + n^2 + n) | O(n^3) | Keep the most dominant term (cubic); lower-order terms are dropped. |
| O(2^n * n!) | O(2^n * n!) | No simplification; exponential and factorial complexities remain. |
| O(n log n + n^2) | O(n^2) | Quadratic growth (n^2) dominates n log n growth. |
These principles provide a foundation for understanding how various operations and code structures contribute to an algorithm's time complexity. They are essential when breaking down and analyzing the performance of algorithms and code.
It's worth noting that while these principles are generally true, there can be exceptions and variations depending on the specific programming language, hardware, and optimizations applied. However, they provide a good starting point for reasoning about algorithmic efficiency.
So, when we simplify O(5n + 2) to O(n), we're essentially saying that as 'n' becomes large, the number of operations grows linearly with 'n,' and the constant term 2 doesn't significantly impact the overall growth rate concerning 'n'. If you want to learn more about simplifying big expressions read this https://medium.com/swlh/lets-simplify-big-o-9aed90d11f34
In Big O notation, we aim to express the upper bound or worst-case scenario of an algorithm's growth rate as a function of 'n' while simplifying the expression by focusing on the most dominant term, ignoring constants, and ignoring lower-order terms. This simplification helps us compare and analyze algorithms more effectively.
Let’s look at a few more algorithms in the https://rithmschool.github.io/function-timer-demo/ tool and try to get their big O notation. So for the countUpAnddown
function countUpAndDown(n) {
console.log("Going up!");
//loop one
for (var i = 0; i < n; i++) {
console.log(i);
}
console.log("At the top!\nGoing down...");
// loop two
for (var j = n - 1; j >= 0; j--) {
console.log(j);
}
console.log("Back down. Bye!");
}
It's understandable to think that because there are two loops in the countUpAndDown function, both with time complexities of O(n), the overall time complexity is 2n. However, when analyzing the time complexity of consecutive loops, we don't simply add their complexities together.
In this case, you have two separate loops, each with its own iteration over 'n.' When determining the overall time complexity, you take the highest time complexity because the loops run sequentially, not concurrently.
So, in this function:
The first loop has a time complexity of O(n).
The second loop also has a time complexity of O(n).
But since they run one after the other, you consider the highest time complexity, which is O(n). This represents the overall time complexity of the function. Therefore, the time complexity of countUpAndDown is O(n), not 2n.
For printAllPairs
function printAllPairs(n) {
for (var i = 0; i < n; i++) {
for (var j = 0; j < n; j++) {
console.log(i, j);
}
}
}
For the nested loops in the printAllPairs function, where you have two loops iterating from 0 to 'n,' the time complexity can be analyzed as follows:
- The outer loop runs 'n' times, and for each iteration of the outer loop, the inner loop also runs 'n' times. This means that for each of the 'n' iterations of the outer loop, the inner loop performs 'n' iterations.
To determine the overall time complexity, you can multiply the number of iterations of the outer loop by the number of iterations of the inner loop:
- 'n' iterations of the outer loop 'n' iterations of the inner loop = n n = n^2
So, the time complexity of the printAllPairs function with nested loops is O(n^2), which is quadratic time complexity. This indicates that the number of operations grows quadratically with the size of 'n,' and it can become significantly slower as 'n' increases.
Space Complexity
So far we have been focusing on time complexity: how can we analyze the runtime of an algorithm as the size of the inputs increases? So good news is we can still use big O notation to analyze space complexity: how much additional memory do we need to allocate in order to run the code in our algorithm
let’s talk about the inputs, so we shall ignore the size of n since it obviously increases with the n. we shall focus on auxiliary space complexity which refers to space required by the algorithm, not including the space taken by the inputs.
A few rules of thumb
Most primitives(Booleans, numbers, undefined, null) are constant space.
Strings require O(n) space (where n is the string length)
Reference types are generally O( n), where n is the length (for arrays) or the number of keys (for objects)
Let’s look at a few examples:
Example 1: sum function
function sum(arr) {
let total = 0;
for (let i = 0; i < arr.length; i++) {
total += arr[i];
}
return total;
}
In this example:
The function
sumtakes an arrayarras input.A single variable
totalis created, which is constant space (O(1)) because it doesn't depend on the size of the input.The loop uses an iterator
i, which is also constant space (O(1)).Now since the
totalis already in memory we don't considertotal += arr[i];The space complexity is primarily determined by the input array
arr. As the array's size increases, the space required to store it increases proportionally. Therefore, the space complexity of this function is O(n), where 'n' is the length of the input array.
Example 2: double function
function double(arr) {
let newArr = [];
for (let i = 0; i < arr.length; i++) {
newArr.push(2 * arr[i]);
}
return newArr;
}
In this example:
The function
doubletakes an arrayarras input.A new array
newArris created, which is directly related to the size of the input array. Asarrgrows, so doesnewArr. Therefore, the space complexity fornewArris O(n), where 'n' is the length of the input array.The loop uses an iterator,
iwhich is constant space (O(1)).
So, for the double function, the primary contributor to space complexity is the new array, newArr making it O(n).
Lastly let’s talk about logarithms
We've explored some of the familiar complexities in Big O notation, such as O(1) for constant time, O(n) for linear time, and O(n^2) for quadratic time. However, as we delve deeper into algorithm analysis, we encounter more intricate mathematical expressions, and one that frequently arises is the logarithm.
Logarithmic time complexity is a desirable characteristic of algorithms because it means that the algorithm's performance improves as the input size increases. Certain searching algorithms, such as binary search, have logarithmic time complexity because they repeatedly divide the search space in half. Efficient sorting algorithms, such as quicksort, merge sort, and heapsort, involve logarithms because they divide the input into smaller and smaller pieces until they are sorted. Recursion sometimes involves logarithmic space complexity because each recursive call adds a new layer to the call stack, which has a logarithmic relationship to the input size.
Resources
Subscribe to my newsletter
Read articles from Atuhaire Collins Benda directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
