Reasoning from First Principles: The Fundamentals of Computation

Table of contents:

• Introduction

• Glossary

• First Principles

• Practice

• Logic Gates (AND, OR, XOR, NAND)

• The Foundations of Addition

• Summary

Introduction

As a developer with experience in C and primarily TypeScript, my interest in blockchain was sparked by the fascinating technology and my drive to understand it deeply. Recently, I was tasked with reviewing and writing a code report on Optimism's PreimageOracle, the most complex challenge I’ve encountered. This experience highlighted the need for me to delve deeper, not just into blockchain, but into the core principles of computing itself.

Glossary

Abstraction: The process of hiding implementation details by creating a simplified interface focusing on functionality rather than underlying logic.

Algorithm: A finite set of steps designed to solve a problem within a finite amount of time and resources.

Bit: A single binary digit can be either 0 or 1, where 0 represents false, and 1 means true.

4-Bit Binary Value: A binary number consisting of four digits (bits), each of which can be 0 or 1. This allows for 16 unique combinations, such as 0000, 0001, 0010, …, 1111.

Truth Table: This outlines the behavior of logic gates by listing all possible input combinations and their corresponding outputs, helping to understand gate operations.

First Principles huh?

Reasoning from first principles is a major factor that differentiates engineers from rookies. “It is the way of looking at the world that involves breaking down things to their most fundamental truths and then reasoning up from there” - Elon Musk.

Often, we operate at a high level of abstraction, like using a computer to add numbers, without fully understanding the underlying mechanics. At its core, computation or any other high-level concepts are simply processes that manipulate a string of bits.

A bit is a single binary digit which is either 0 or 1. 0 in logic is false, and 1 is true.

Let’s Practice

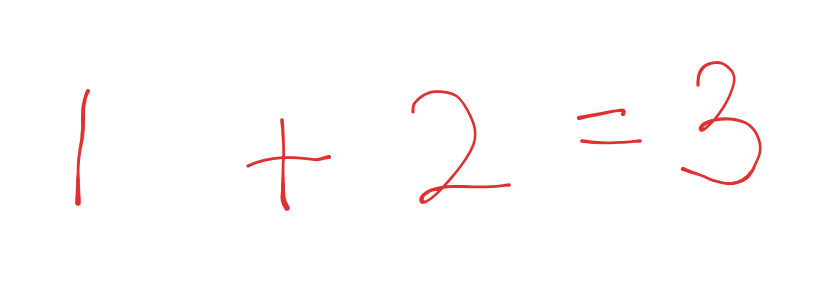
Addition is the most basic form of computation, involving the computer summing two numbers to produce an output. However, the computer only understands binary code, which consists of 0s and 1s. So, how does this work?

For instance, when we want to add the numbers 1 and 2, both numbers are first converted into binary format. Then, the addition is performed in binary and returns a binary output.

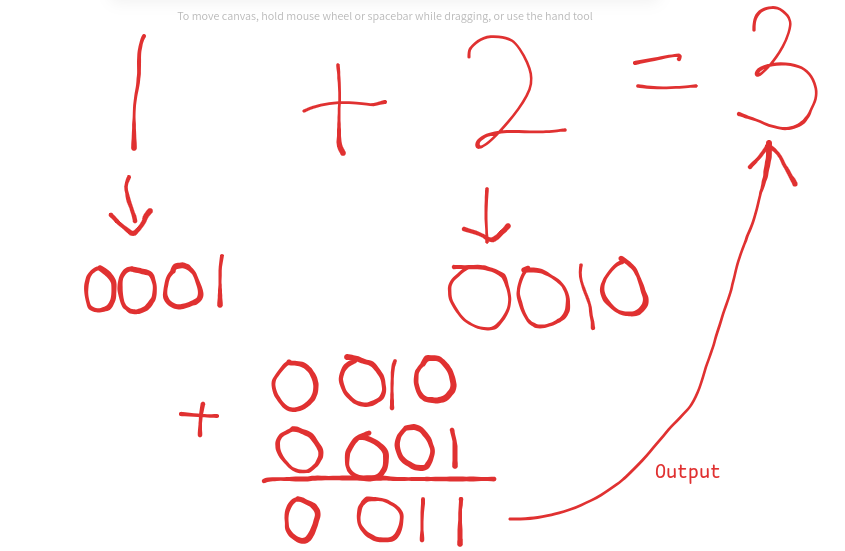
In the addition example above, the decimal numbers are converted to a 4-bit binary value. We've established that computers only understand 0s and 1s, but do they understand addition?

Certainly not! Don't be surprised; I just realized this myself a few weeks ago. Computers do not understand addition, subtraction, or any computations. Remember, we are exploring deeper concepts and will uncover new insights along the way!

How do computers perform addition, subtraction, and other basic arithmetic operations?

They utilize logic gates to perform these operations!

Enter Logic Gates

Logic gates are the building blocks of computation and digital circuits. A computer, as a complex digital device, is made up of many digital circuits.

Understanding logic gates means knowing what the computer was built on.

We will start with basic gates and build up to more complex ones.

We will look into logic gates design, truth tables, and how they are put together.

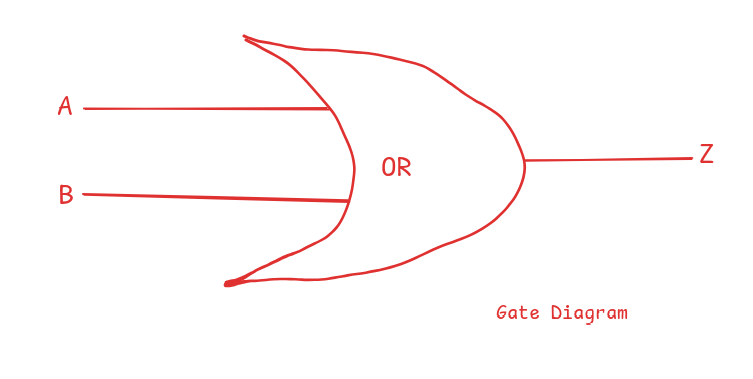
OR gate

This acts like an addition operator. As long as one of its inputs is true, its output is true.

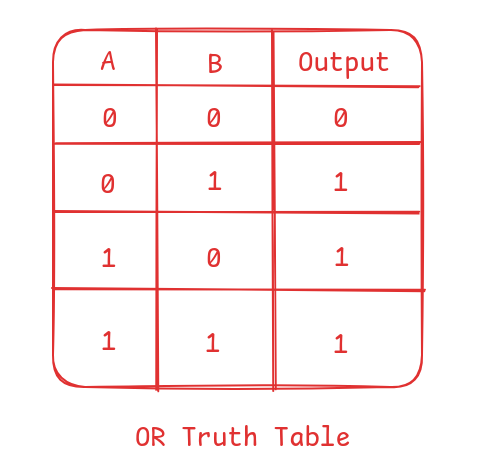
Based on the table above, we see that:

0 OR 1 = 1 is very similar to 0 + 1 = 1

But 1 OR 1 = 1 differs from 1 + 1 = 2. It's important to recognize these key differences and remain curious as we explore how addition works behind the scenes.

AND gate

This acts exactly as the multiplication operator. It only returns true when both inputs are true.

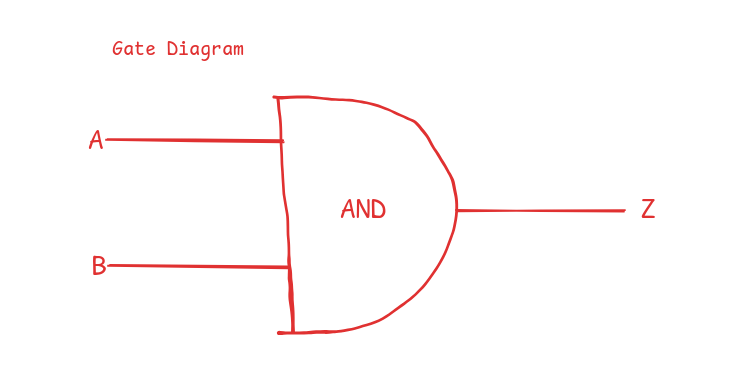
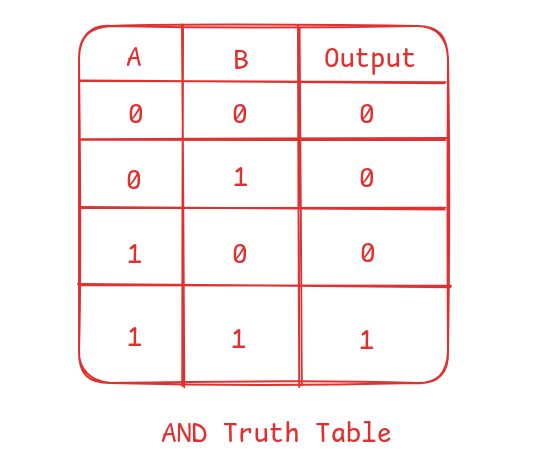
0 AND 1 = 0, 0 × 1 = 0

1 AND 1 = 1, 1 × 1 = 1

Knowing that AND works like multiplication is the cheat code to remembering its truth table.

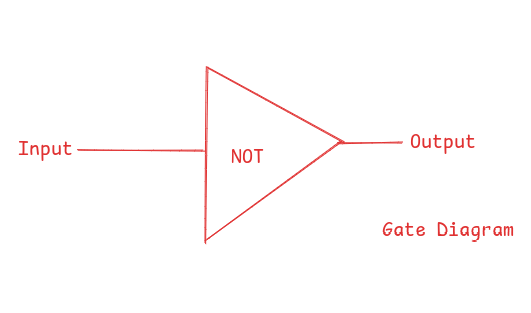
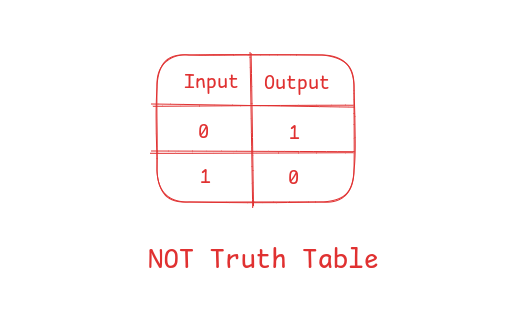
NOT gate

This returns the opposite or negation of the input.

NAND gate

This is the most fundamental logic gate. All other gates can be built from NAND gates. Just as prime numbers are the building blocks of the number system, NAND gates are the building blocks of all other logic gates.

Why didn’t this article start with NAND then? Well, there are 2 perspectives to gates; Logical and Electrical. Logically, the NAND gate works exactly like the opposite of the AND gate, so to understand the NAND gate, you need a basic reminder of how AND works. If the article started with the NAND gate, we would need to talk about the electrical workings of the gate which makes it the fundamental gate but that is beyond the scope of this article!

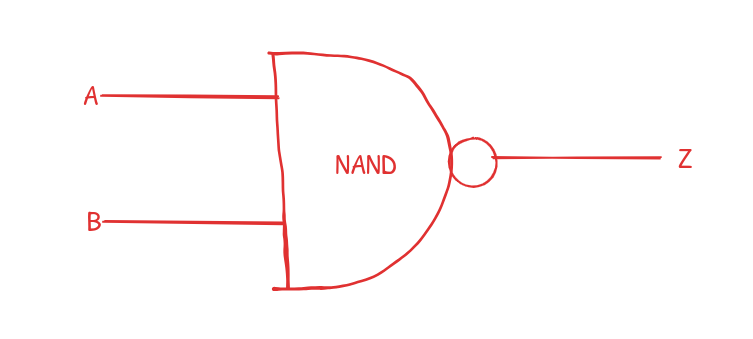
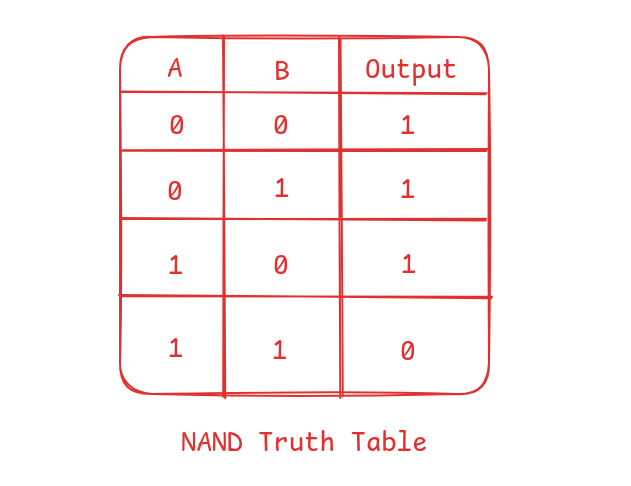
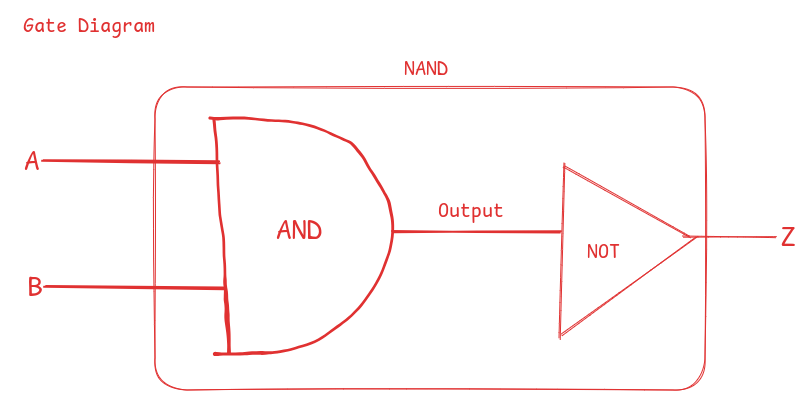
Logically, NAND is like the combination of the AND and NOT gate.

From the truth table, we see that:

0 NAND 0 = 1, how?

1. 0 AND 0 = 0

2. NOT 0 = 1

Thus, the result is 1. Try using other input values and follow these steps to find the output.

Note: NAND gates natively are not derived from AND and NOT gates, instead, AND, NOT and all other gates are built from NAND gates but the explanation above was only used to explain the working of the NAND gate.

XOR gate

Its full name is Exclusive OR Gate. XOR only returns true when both inputs are not the same.

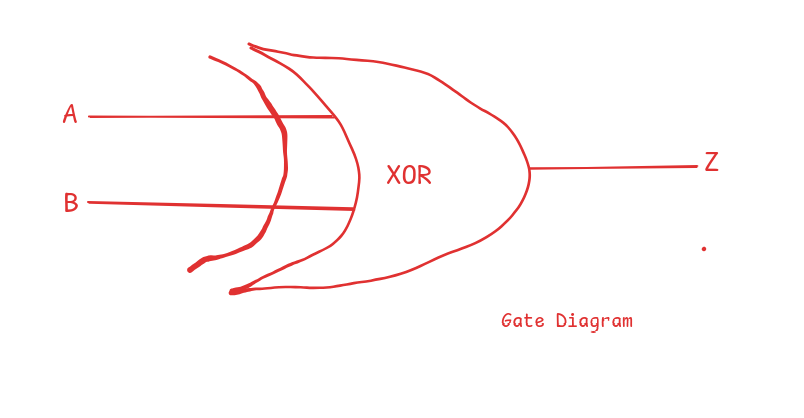
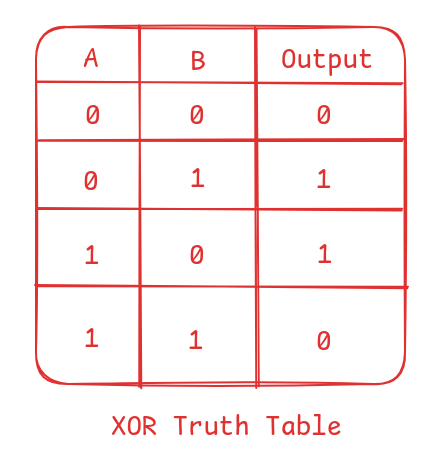
The Foundations of Addition

Let’s examine two additions:

1. 1 + 2 = 3

2. 9 + 5 = 14

Earlier, we converted the decimals to 4-bit digits so both cases are now:

1. 0001 + 0010 = 0011

2. 1001 + 0101 = 1110

The conversion of decimals to binary can be done using successive division or expansion methods. For more check testbook

Instance 1

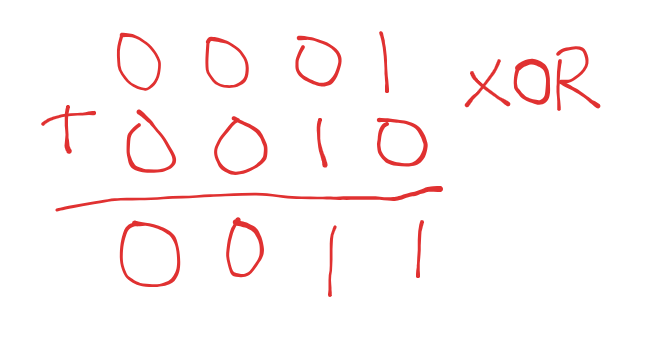
Usually when adding, we start from the last digit on the right, and then keep adding until we get to the leftmost part of the digit. In terms of bits, the rightmost part is called the LSB (least significant bit), and the leftmost part is the MSB (most significant bit), more on this later.

In the diagram above, we do (forgetting the carry part):

1. 1 + 0 = 1

2. 0 + 1 = 1

3. 0 + 0 = 0

4. 0 + 0 = 0

This operation is exactly XOR, remember that XOR gate only returns true (1) when both inputs are opposites. So basically:

1. 1 + 0 => 1 XOR 0 = 1

2. 0 + 1 => 0 XOR 1 = 1

3. 0 + 0 => 0 XOR 0 = 0

4. 0 + 0 => 0 XOR 0 = 0

This works correctly!

Instance 2

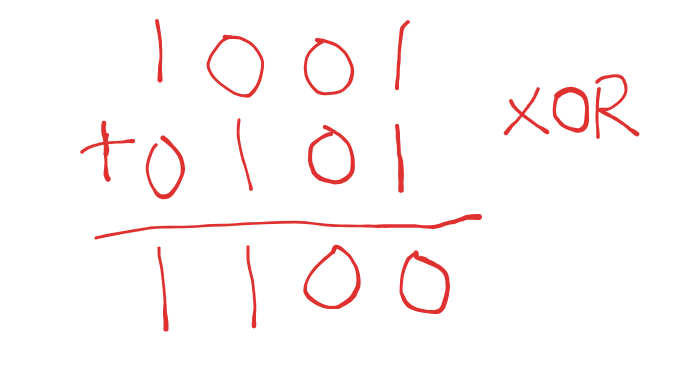
Let’s apply the XOR logic we learned earlier here!

1. 1 XOR 1 = 0

2. 0 XOR 0 = 0

3. 0 XOR 1 = 1

4. 1 XOR 0 = 0

Surprisingly our result here is not as expected, we got 1100 which in decimal is 12 meanwhile our expected result was 14 which is 1110 in binary. What went wrong?

Let’s do the addition normally without the XOR gate and then we can spot the bug

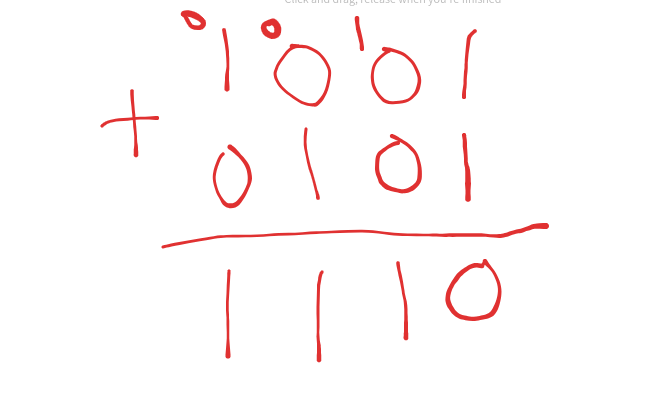
The bug was the carry bits or what we sometimes call the remainders.

1. 1 + 1 = 0 R 1, so we have a carry bit = 1

2. (prev carry bit) 1 + 0 + 0 = 1 R 0, we have zero carry bit

3. (prev carry bit) 0 + 1 = 1 R 0, we have zero carry bit

4. (prev carry bit) 1 + 0 = 1 R 0, we have zero carry bit

5. There are no extra digits to add so we discard the carry bit. Note we discard the carry bit no matter what the value is because according to our calculation, we are dealing with 4-bit binary values, suppose that the carry bit was 1, adding it to the result will extend it to 5-bit which is beyond our measurement scope. By default, the computer trims off the extra carry bit.

Notice that we only have carry or remainders when both digits are 1, the carry bit is zero everywhere else. Which gate has that behavior? Yes! The AND gate.

Let’s combine both gates and see again what the algorithm is:

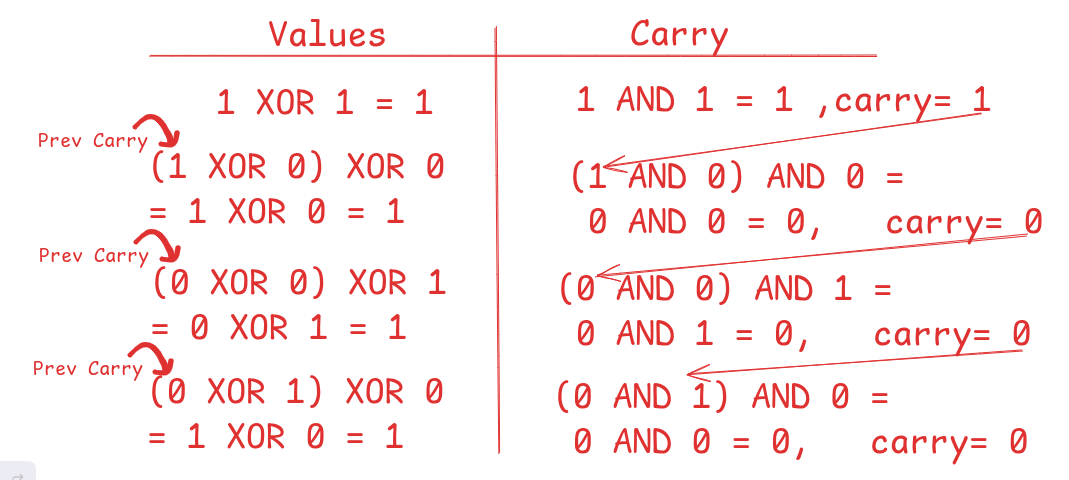
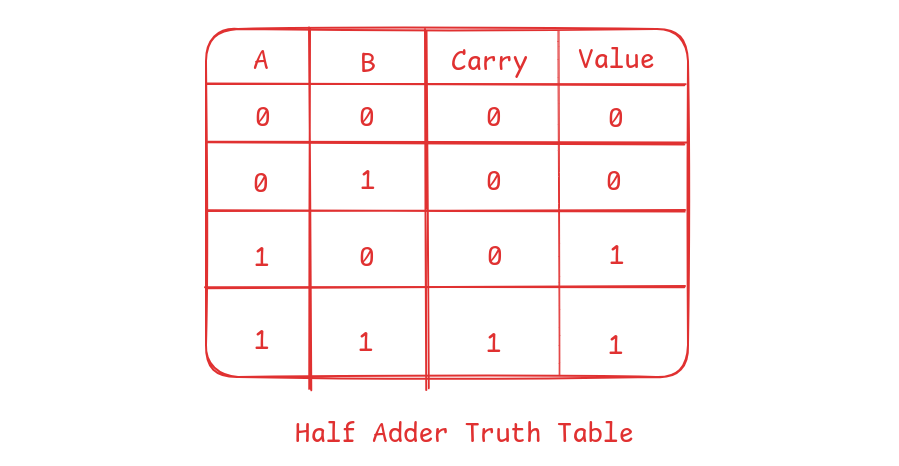
From the diagram above, we see that we repeat the same process multiple times until there are no more digits to add. We get the value using XOR and the carry bit using AND, and we keep reusing the operation. This operation is called a Half Adder.

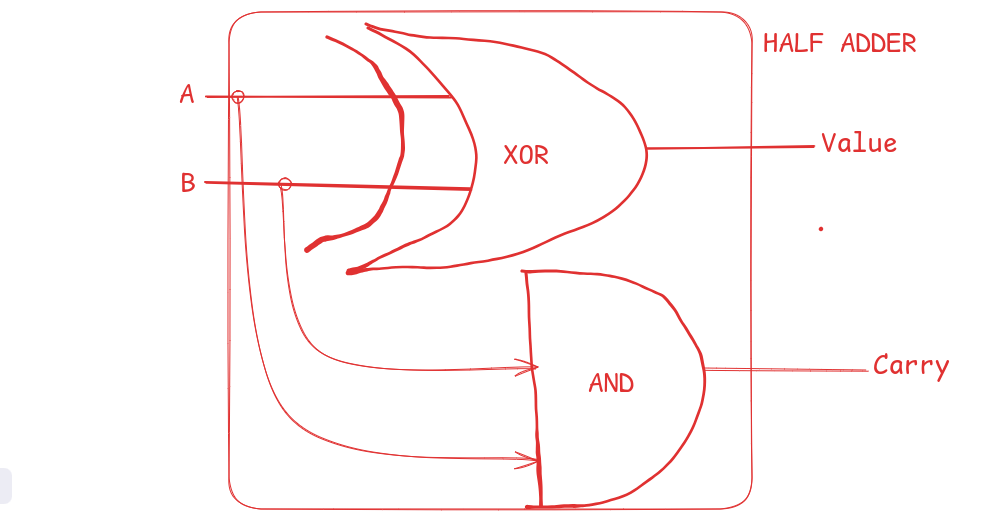
The combination of several Half Adders gives a Full Adder which is exactly what the computer uses to perform addition operation.

Summary

We have explored in depth how a computer performs addition from the ground up and it is an XOR and AND gate performing so-called ‘addition operation‘ under the hood. Like many other operations such as machine learning and data storage, this can be broken down into basic principles and understood from there.

Congratulations on reaching this point! You have learned a fundamental concept that at least 50-70% of people, including some programmers and computer science students, don't know.

Never forget that a computer is just a machine that manipulates bits using specific algorithms (logic) defined in software and executed. In my next article, I will explore the concepts of MSB, LSB, and even storage! Reasoning and approaching problems from a first principles approach will always make you stand out!