Swift. Numbers. And their limits (Part 2)
 Stanislav Kirichok
Stanislav Kirichok
This time, we’re talking about floating-point numbers: Float (including its variations like Float16, Float32, Float64, and the elusive Float80) and Double.
Storage
So, what’s a floating-point number, you ask? It’s that number that sits between two integers, telling you exactly how far it is from the smaller one with its fractional part, always aiming for precision(not always successfully).
Its internal structure and how it’s stored in memory is quite different from the straightforward world of integers.
Let’s take a closer look at the smallest of the floating-point family: Float16 (half-precision, if you know what that means already, you can probably skip the rest of this article :) ). For the rest of us, let’s break it down.
First off, we reserve 1 bit for the sign. As always, 0 means the number is positive, and 1 means it’s negative.
Next, we have the two main parts: significand(also called mantissa) and exponent.
Significand: This is where the real value of the number lives. It’s what determines the precision of the type. For Float16, we have 10 bits set aside for the significand. When the number isn’t zero, infinity, or NaN, the significand is normalized to be between 1 and 2(not included).
Exponent: This part tells us where to place the decimal point (well, technically, the binary point). For Float16, we have 5 bits reserved for the exponent. It’s the part responsible for how large or small the number can get.
The following formula can be used to calculate the full floating-point number from its components:
$$(1)\ Value = significand * radix^{exponent}$$
The radix is 2 for floating-point numbers, as defined by the IEEE 754 standard. This makes sense, given that everything is stored in binary. Essentially, a floating-point number is the significand multiplied by 2 raised to the power of the exponent.
Let’s go through an example: 123.4. To fit this into the floating-point format, we’ll keep dividing the number by 2 until it falls within the range 1..<2.
| Attempt | Result |
| 1 | 61.7 |
| 2 | 30.85 |
| 3 | 15.425 |
| 4 | 7.7125 |
| 5 | 3.85625 |
| 6 | 1.928125 |
This means the exponent should be 6, and the significand is approximately 1.928125. It’s seemingly clear for the exponent, but it’s still unclear how to represent another floating-point number in binary. Let’s set the significand aside for a moment and focus on the exponent.
The exponent is definitely an integer, but there’s a catch. If the resulting float is greater than 2, the exponent will be positive; otherwise, it will be negative! But we don’t want to spend another bit just for the sign. That’s where the bit-saver comes in: exponent bias. This value is added to the calculated exponent to ensure it's always positive. Positive thinking at its best!
What bias should we have for Float16?
The Float16 exponent is 5 bits wide, which means it can represent 32 values (since 2=2^5=32). However, we need to reserve two of these values for special cases:
| Stored exponent | Significand | Value |
0 (00000) | 0 | zero |
0 (00000) | ≠ 0 | subnormal |
31 (11111) | 0 | infinity |
31 (11111) | ≠ 0 | NaN (Not-a-Number) |
Putting it all together: the exponent is represented as an unsigned binary number with a width of 5 bits, where 0 and 31 are reserved. This leaves us with 30 usable values that must be split between positive, negative, and zero. And yes, we still need an exponent of zero for cases where the final Float16 value is exactly equal to the significand.
Let’s split the 30 values into two halves: 15 and 15. One part will include zero, but which side should it be? Should we have the range −15…14 with a bias of 16, or -14…15 with a bias of 15?
The IEEE 754 standard chose -14…15 with a bias of 15. The likely reason for this is that we generally deal more with large floating-point numbers than very small ones.
Now, let’s calculate the stored binary value for the exponent:
If the real exponent is 6, we add the bias of 15, giving us a stored exponent of 21, or 10101 in binary. Let’s verify this with the special properties available for all floating-point types:
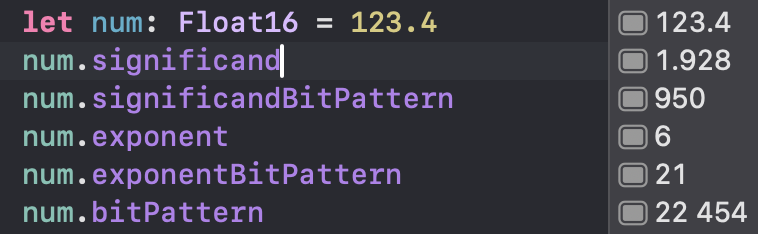
As you can see, everything matches our conclusions and calculations. We can even spot the exponent part in the overall bitPattern. The seemingly mysterious 22454 becomes clear when converted to binary: 101011110110110. This is simply the concatenation of the exponent and significand.
10101(21) & 1110110110(950)
So far, so good. Now, we face the final challenge: how do we fit 1.928125 into the 10 available bits?
Here’s the first trick: we don’t need to store the integer part. Since the number is always normalized to the range 1..<2, the integer part is always 1. This is called the implicit bit, and it doesn’t need to be stored, saving us some space.
Second trick (and the final one): Since we’ve already removed the integer part, we’re left with just the fractional part, ranging from 0 to 1 (exclusive). We can store this as an unsigned integer in the range 0…1023 (the max value for 10 bits is 1111111111).
There's a standard algorithm for converting the fractional part of a decimal number to its binary representation:
Multiply the fractional part by
2Record the integer part (
0or1) as the next bit in the binary sequenceUse the new fractional part (after subtracting the integer part) for the next iteration.
Repeat steps 1-3 until you have the desired number of bits or the fractional part becomes zero.
Let’s put it into the table:
| Bit Index | Value | Bit value |
| - | 0.928125 | - |
| 0 | 1.85625 | 1 |
| 1 | 1.7125 | 1 |
| 2 | 1.425 | 1 |
| 3 | 0.850 | 0 |
| 4 | 1.7 | 1 |
| 5 | 1.4 | 1 |
| 6 | 0.8 | 0 |
| 7 | 1.6 | 1 |
| 8 | 1.2 | 1 |
| 9 | 0.4 | 0 |
So, binary significand is 1110110110(950). We didn’t reach correct representation but rather ran out of available bits to store more precise result. Moreover, it is not possible at all. If you look closely to latest values starting from index 5 you will see repeating pattern that will never converge to 1.
Nevertheless, this result matches exactly with the values provided by Swift.
Let’s double check using Formula 1:
Converting our binary significand back to decimal:
0.927734375Adding back implicit integer part:
1.927734375Exponent was 6, so
1.927734375 × 2^6= 123.375
Our initial value was 123.4. Indeed it was not possible to represent it in binary precisely so we have this inaccuracy: (123.4 - 123.375) / 123.4 = 0.02%
Limitations
As you can see from how floating-point numbers are stored, their capacity is limited. But unlike integers, this limitation doesn’t just lead to maximum and minimum bounds—it can also result in unexpected precision loss. This means that certain decimal values might be stored as binary approximations that differ slightly from the original decimal value, leading to small but sometimes significant differences.
Previous chapter showed how we can see and calculate such differences. Now we will investigate another source of precision loss—the accumulation of errors.
Let’s take 0.1 + 0.2 (again stored in Float16).
The precision error for each of them is the same (calculated in the way discussed in the previous part of this article): 0.024414%.
But when we calculate the same error for the result of 0.1 + 0.2—which should obviously be 0.3—we receive 0.2998046875 with an error of 0.065104%, which is more than twice the error of each component.
This error can be reduced by using more precise types like Float or Double but cannot be eliminated entirely.
Overflow and underflow
Overflow occurs when a calculation produces a value larger than the maximum representable value of a floating-point type. Similarly, underflow happens when a value is closer to zero than the smallest representable nonzero value.
Overflow is straightforward for floating-point numbers in Swift. When we exceed the maximum representable value for a Float, we receive positive infinity (inf) as the result. If the value is negative, the result will be negative infinity (-inf).
let overflowPositive = Float16.greatestFiniteMagnitude * 2
print(overflowPositive) // Outputs: inf
let overflowNegative = -Float16.greatestFiniteMagnitude * 2
print(overflowNegative) // Outputs: -inf
Underflow is different. Let’s take the smallest positive normal value that we can represent with Float16:
Float16.leastNormalMagnitude with following properties:
|
|
|
|
| -14 |
|
|
|
|
Using these properties, we can calculate the real decimal value represented by this binary number: 1 × 2 ^ -14 = 0.000061.
What will happen if we divide it by 2?
Float16.leastNormalMagnitude / 2:
significand |
|
|---|---|
significandBitPattern |
|
exponent |
|
exponentBitPattern |
|
bitPattern |
|
calculated Decimal value | 0.000031 |
Well, we still have some number, and it even looks close to the correct one (expected value is 0.0000305 with an error of 0.057633%). If we check our table with special cases, we can find a row where the exponent is 0 but the significand is not zero, introducing the mysterious subnormal numbers. We sacrifice one bit of the significand after another to expand the value of the exponent by 1 each time. These numbers allow us to keep going with small number calculations at the price of increased inaccuracy. But obviously, they also have their limit.
Please welcome our border tsar Float16.leastNonzeroMagnitude .
significand | 1 |
significandBitPattern | 0000000001(10 bits) |
exponent | -24(getting bigger as significand becomes insignificant) |
exponentBitPattern | 0 |
bitPattern | 0 00000 000000001(16 bits) |
| calculated Decimal value | 0.00000005960464477539063 |
Float16.leastNonzeroMagnitude is smaller than Float16.leastNormalMagnitude by a factor of 1024, which is exactly the bit size of the significand.
Okay, but what should we do with Float16.leastNormalMagnitude / 2?
significand | 0 |
significandBitPattern | 0000000000(10 bits) |
exponent | -9,223,372,036,854,775,808(not sure what Swift wants to tell with such value, but it is Int64.min) |
exponentBitPattern | 00000(5 bits) |
bitPattern | 0 00000 0000000000(16 bits) |
| calculated Decimal value | 0 |
As the significand and exponent are both zero, it means we've reached our final destination: the value zero. You can't go any further from it. You can try to divide Float16.leastNonzeroMagnitude by a number of any arbitrary magnitude, but the result is the same—ZERO. This switch from meaningful values to zero is very important when we deal with any sort of multistep arithmetic operations, like calculating predictive models or other scientific and financial applications.
Dividing a non-zero floating-point number by zero results in positive or negative infinity. However, dividing zero by zero or performing indeterminate operations like subtracting infinity from infinity results in NaN—Not a Number.
To sum up:
Integers resemble a single chain of whole numbers stretching out from zero in both positive and negative directions within their representable range. Using special overflow operators, we can eventually close them up in a circle, where the biggest positive number wraps around to become the smallest negative one upon overflow, and vice versa.
At the same time, floating-point values look like a double chain of positive and negative numbers that run in parallel—from zero to subnormal, from subnormal to normal, and from normal to positive and negative infinity.

Next time, we'll dive into Swift's most precise type to understand how it was built.
Subscribe to my newsletter
Read articles from Stanislav Kirichok directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
