Marching Cubes: Insights into 3D Renderings

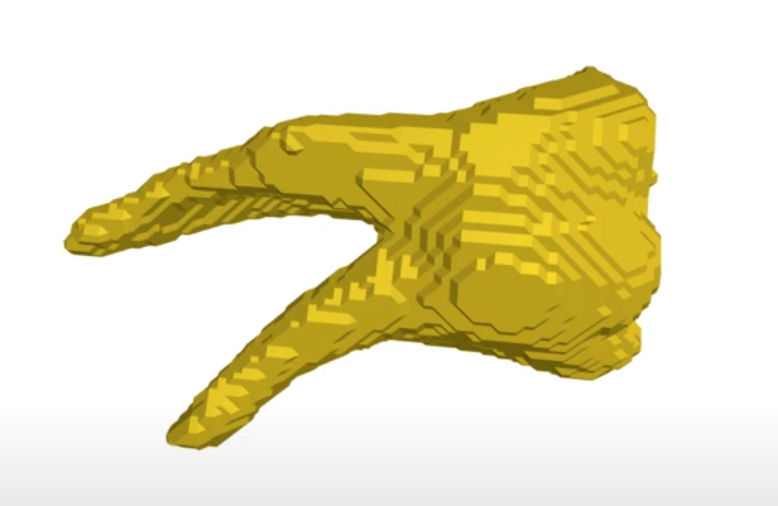
Overview of the Marching Cubes Algorithm

Marching Cubes is a computer graphics algorithm used for extracting a polygonal mesh from a three-dimensional scalar field (such as a volumetric data set).

In simple words, it takes in list of numbers and converts it into a 3D image.

The key idea is to take a 3D list of integers (often binary) and create a smooth surface that approximates a particular value, known as an isovalue. This is commonly used for representing things like boundaries in volume data.

Basic Steps of the Marching Cubes Algorithm

1. Divide the volume into a grid of cubes:

   • A 3D volume (e.g., a CT scan) is typically represented as a grid of scalar values, often stored as a 3D matrix.

   • Each cube is defined by eight neighboring points, or vertices, in the grid. These are the corner points of a cube, typically indexed as:

     

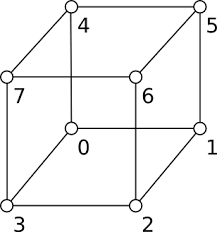
     These eight values are sampled from the scalar field.

2. Classify each cube based on the scalar values:

   • For each cube, the algorithm examines the scalar values at the eight vertices.

   • The algorithm checks whether each vertex value is greater than or less than the isovalue (the threshold level). This results in a binary classification for each vertex.

   • This gives a total of 256 possible configurations.

3. Use a lookup table for triangulation:

   • There are 256 possible ways that a cube can be intersected by the isosurface, but due to symmetry, the number of unique cases can be reduced to 15 distinct patterns.

     

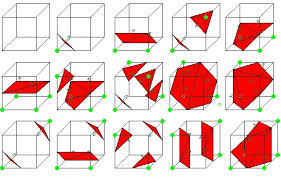
   • The Marching Cubes algorithm uses a lookup table that encodes how to create triangles for each of these configurations. The lookup table contains the edges of the cube that are intersected by the isosurface and specifies how to generate triangles on those edges.

4. Smooth transitions (optional):

   • In some implementations, interpolation is used to refine the placement of the surface between the cube’s vertices. This is commonly done by interpolating the scalar values along the intersected edges to more accurately position the intersection.

5. Mesh generation:

   • After processing all the cubes in the volume, a polygonal mesh is constructed from the generated triangles. This mesh approximates the surface that represents the isovalue.

Advantages of Marching Cubes

• Efficiency: The Marching Cubes algorithm is relatively efficient due to the use of the lookup table, which reduces the need for complex case-by-case checks.

• Flexibility: It works well with any scalar field and can be applied to a variety of types of 3D data, such as volume data from medical imaging, geological modeling, and fluid simulations.

• Quality of output: When correctly implemented, the algorithm produces a smooth and accurate approximation of an isosurface.

Limitations

• Ambiguities: The algorithm has inherent ambiguities in some configurations. For instance, there are cases where the way to triangulate the cube isn't unique (e.g., multiple valid triangulations for the same set of edge intersections). These ambiguities must be resolved to ensure consistency.

• Non-manifold surfaces: If not handled properly, Marching Cubes may produce non-manifold meshes (e.g., where the surface "folds back on itself" or where two triangles share more than one edge).

• Resolution dependent: The quality of the resulting mesh depends on the resolution of the voxel grid. Higher resolution grids generate more detailed surfaces but also require more computational resources.

Applications

• Medical Imaging: Marching Cubes is commonly used to extract 3D models of anatomical structures from 3D image data obtained from CT scans or MRI scans.

• Geology: The algorithm can be used to extract geological surfaces (e.g., terrain modeling) from 3D scalar data.

• Scientific Visualization: It’s used for visualizing data from simulations of physical phenomena like fluid dynamics or molecular simulations.

Conclusion

The Marching Cubes algorithm is a fundamental tool in computational geometry and 3D visualization for converting scalar data into polygonal models. Despite some limitations, its use of a lookup table makes it a highly efficient and widely adopted algorithm, especially in fields like medical imaging and scientific visualization.