Understanding Stationarity, Dickey-Fuller Test in Time Series Analysis: An In-Depth Guide
 Sai Prasanna Maharana
Sai Prasanna Maharana
In time series analysis, stationarity is a fundamental concept that significantly impacts the modeling and forecasting of data. This guide will delve into the concepts of stationarity and non-stationarity, the Dickey-Fuller test for stationarity, methods to convert non-stationary data to stationary, and techniques to detect autocorrelation and seasonality. We'll include practical Python code snippets to illustrate these concepts.
Table of Contents
Introduction to Stationarity
What is Stationarity?
A stationary time series is one whose statistical properties such as mean, variance, and autocorrelation are constant over time. In other words, the time series does not exhibit trends, seasonality, or other structures that change over time.
Types of Stationarity
Strict (Strong) Stationarity: All statistical properties of the time series are invariant to time shifts.
Weak (Second-Order) Stationarity: The mean and variance are constant over time, and the covariance between two time periods depends only on the lag between them, not on the actual time at which the covariance is computed.
Why is Stationarity Important?
Modeling Assumptions: Many time series modeling techniques, such as ARIMA, assume that the underlying series is stationary.
Predictability: Stationary series are easier to predict because their statistical properties are stable over time.
Statistical Inference: Non-stationary data can lead to invalid or misleading statistical inferences.
Non-Stationarity
Causes of Non-Stationarity
Trends: Long-term increase or decrease in the data.
Seasonality: Regular patterns repeating over time.
Structural Breaks: Changes in the underlying process generating the data.
Heteroscedasticity: Variance of the series changes over time.
Examples of Non-Stationary Series
Economic Indicators: GDP, inflation rates, stock prices.
Environmental Data: Temperature readings over decades.
Social Data: Population growth over time.
Dickey-Fuller Test
What is the Dickey-Fuller Test?
The Dickey-Fuller (DF) test is a statistical test that checks for the presence of a unit root in a univariate time series sample. The presence of a unit root indicates that the time series is non-stationary.
Why and When to Use It
Purpose: To determine whether differencing is required to achieve stationarity.
When to Use: Before fitting models that assume stationarity, such as ARIMA.
Interpreting the Results
Null Hypothesis (( H_0 )): The time series has a unit root (non-stationary).
Alternative Hypothesis (( H_1 )): The time series is stationary.
Decision Rule:
If the p-value is less than the significance level (e.g., 0.05), reject ( H_0 ).
If the test statistic is less than the critical value, reject ( H_0 ).
Converting Non-Stationary Series to Stationary
Differencing
Definition: Subtracting the previous observation from the current observation.
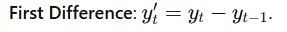
Higher-Order Differences: Applying differencing multiple times if needed.
Detrending
Definition: Removing the underlying trend component from the time series.
Methods:
Subtracting the Trend Line: Fit a regression line and subtract it.
Moving Average Smoothing: Use moving averages to estimate the trend.
Deseasonalizing
Definition: Removing the seasonal component from the time series.
Methods:
Seasonal Decomposition: Using methods like STL (Seasonal-Trend Decomposition using Loess).
Seasonal Differencing: Differencing the series at seasonal lags.
Detecting Autocorrelation and Seasonality
Autocorrelation Function (ACF)
Purpose: Measures the correlation between the time series and its lagged values.
Usage: Identify the presence of autocorrelation and seasonal patterns.
Partial Autocorrelation Function (PACF)
Purpose: Measures the correlation between the time series and its lagged values, controlling for the effects of intermediate lags.
Usage: Helps in identifying the order of autoregressive terms.
Seasonal Decomposition
Purpose: Decompose the time series into trend, seasonal, and residual components.
Methods: Additive or multiplicative models, STL decomposition.
Practical Implementation with Python
Let's apply these concepts using Python libraries such as pandas, numpy, matplotlib, and statsmodels.
Data Preparation
Import Libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# Statistical libraries
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.seasonal import seasonal_decompose
Generate Synthetic Non-Stationary Data
We'll create a time series with trend and seasonality.
# Create date range
dates = pd.date_range(start='2010-01-01', periods=120, freq='M')
# Generate data components
np.random.seed(42)
trend = np.linspace(10, 50, 120)
seasonality = 10 * np.sin(np.linspace(0, 3 * np.pi, 120))
noise = np.random.normal(0, 2, 120)
# Combine components
data = trend + seasonality + noise
# Create DataFrame
df = pd.DataFrame({'Date': dates, 'Value': data}).set_index('Date')
Visualize the Time Series
plt.figure(figsize=(12, 6))
plt.plot(df['Value'], label='Time Series')
plt.title('Non-Stationary Time Series with Trend and Seasonality')
plt.xlabel('Date')
plt.ylabel('Value')
plt.legend()
plt.show()
Testing for Stationarity
Perform Dickey-Fuller Test
def adf_test(series, title=''):
"""
Perform Augmented Dickey-Fuller test.
"""
print(f'Augmented Dickey-Fuller Test: {title}')
result = adfuller(series.dropna(), autolag='AIC')
labels = ['Test Statistic', 'p-value', '# Lags Used', '# Observations Used']
out = pd.Series(result[0:4], index=labels)
for key, val in result[4].items():
out[f'Critical Value ({key})'] = val
print(out.to_string())
if result[1] <= 0.05:
print("=> Reject the null hypothesis. The series is stationary.")
else:
print("=> Fail to reject the null hypothesis. The series is non-stationary.")
adf_test(df['Value'], 'Original Series')
Interpretation
The p-value is likely to be greater than 0.05, indicating non-stationarity.
Converting to Stationary
Differencing
First Difference
df['First Difference'] = df['Value'] - df['Value'].shift(1)
adf_test(df['First Difference'], 'First Difference')
Seasonal Difference
df['Seasonal Difference'] = df['Value'] - df['Value'].shift(12)
adf_test(df['Seasonal Difference'], 'Seasonal Difference')
First Seasonal Difference
df['First Seasonal Difference'] = df['First Difference'] - df['First Difference'].shift(12)
adf_test(df['First Seasonal Difference'], 'First Seasonal Difference')
Detrending
Using Linear Regression
from sklearn.linear_model import LinearRegression
# Prepare data
df['Time'] = np.arange(len(df.index))
X = df[['Time']]
y = df['Value']
# Fit linear regression
model = LinearRegression()
model.fit(X, y)
# Calculate trend
df['Trend'] = model.predict(X)
# Detrend
df['Detrended'] = df['Value'] - df['Trend']
adf_test(df['Detrended'], 'Detrended Series')
Deseasonalizing
Using Seasonal Decomposition
# Decompose the time series
decomposition = seasonal_decompose(df['Value'], model='additive', period=12)
# Extract seasonal component
df['Seasonal'] = decomposition.seasonal
# Deseasonalize
df['Deseasonalized'] = df['Value'] - df['Seasonal']
adf_test(df['Deseasonalized'], 'Deseasonalized Series')
Detecting Autocorrelation and Seasonality
Plot ACF and PACF
# Original Series
fig, ax = plt.subplots(2, 1, figsize=(12, 8))
plot_acf(df['Value'].dropna(), lags=50, ax=ax[0])
plot_pacf(df['Value'].dropna(), lags=50, ax=ax[1])
plt.tight_layout()
plt.show()
Interpretation
ACF Plot: Shows high autocorrelation at various lags, indicating non-stationarity and seasonality.
PACF Plot: Helps determine the order of autoregressive terms.
Conclusion
Stationarity is crucial for time series modeling as many models assume the series is stationary.
Dickey-Fuller Test helps determine whether a series is stationary.
Differencing, detrending, and deseasonalizing are techniques to convert a non-stationary series into a stationary one.
Autocorrelation and seasonality can be detected using ACF and PACF plots, as well as seasonal decomposition.
By transforming the data to achieve stationarity and understanding its underlying components, we can build more accurate and reliable forecasting models.
References
Time Series Analysis by James D. Hamilton
Forecasting: Principles and Practice by Rob J Hyndman and George Athanasopoulos
Statsmodels Documentation: Time Series Analysis
Subscribe to my newsletter
Read articles from Sai Prasanna Maharana directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
