From Cosine to Dot: Benchmarking Similarity Methods for Speed and Precision

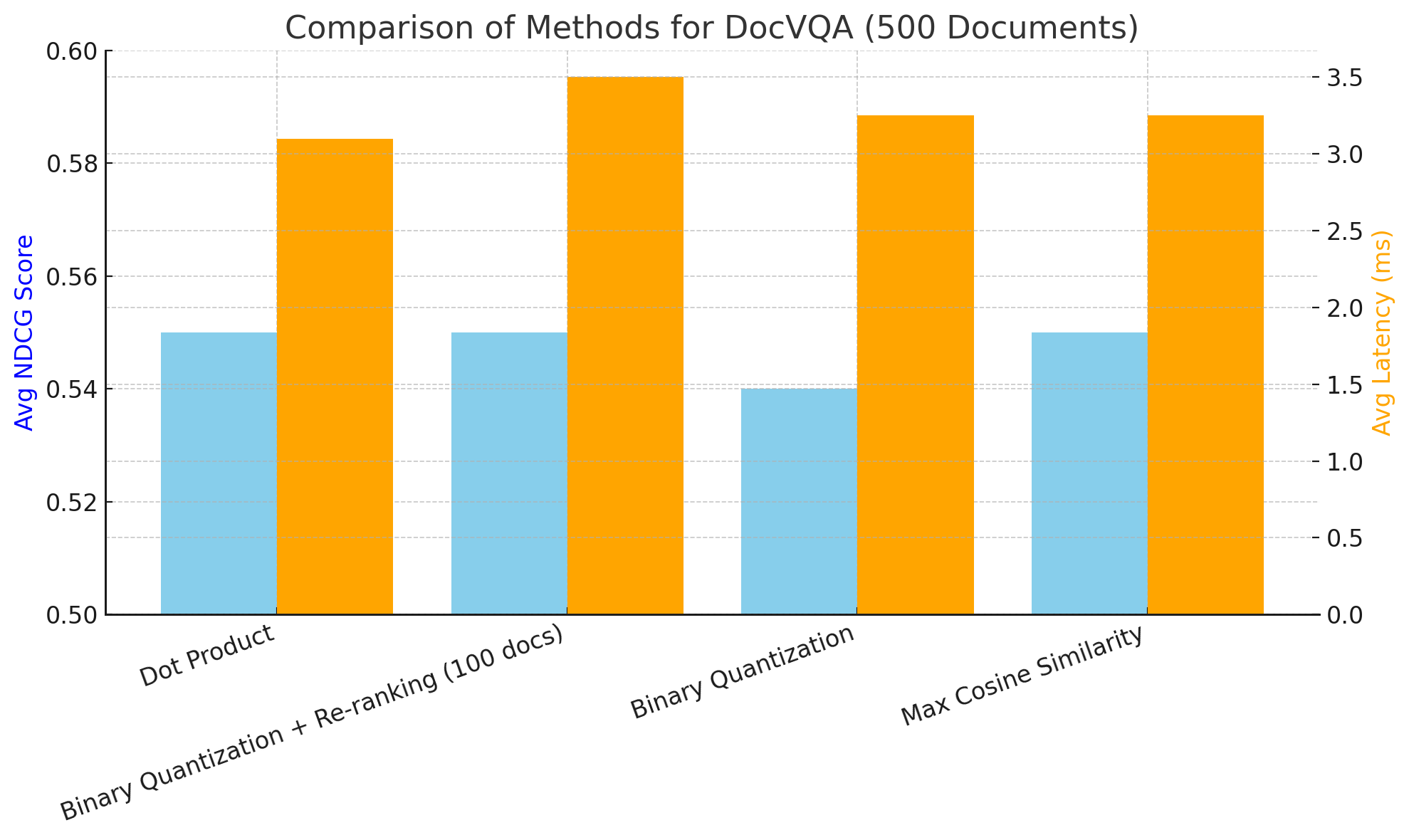
Background

Retrieval Augmented Generation (RAG) empowers large language models (LLMs) by integrating private documents and proprietary knowledge, unlocking their potential for nuanced and informed responses. However, efficiently extracting information from unstructured documents—especially those with complex visual layouts—remains a significant challenge.

The conventional approach to handling visually dense documents typically involves a multi-stage process: Optical Character Recognition (OCR) to extract text, Layout Recognition to understand the document structure, Figure Captioning to interpret images, Chunking to segment the text, and finally, Embedding to represent each segment in a vector space. This pipeline is not only complex and computationally demanding but also prone to error propagation. Inaccuracies in any stage, for example, OCR errors or misinterpretation of visual layouts, can significantly degrade the quality of downstream retrieval and generation.

A more streamlined approach, as pioneered in the ColPali paper, leverages the power of vision models. Instead of complex pre-processing, this method directly embeds entire document pages as images, simplifying the retrieval process to a similarity search on these visual embeddings. This approach eliminates the need for laborious pre-processing steps and potentially captures richer contextual information from the visual layout and style of the document. This innovative approach forms the foundation of our work in ColiVara.

This post details our research on optimizing and benchmarking various similarity calculation methods, building upon and extending the core ideas presented in ColPali.

We store vector embeddings in a PostgreSQL database, employing a one-to-many relationship between vectors and their corresponding pages.

Research Question

The ColPali paper uses the late-interaction style computations to calculate the relevancy between a query and documents. The question we wanted to answer, could we get the same results using other similarity computations with better latency?

Our metric, to stay consistent with the paper was the NCDG@5 score in DocVQA and our typical API request latency using:

• Late-interaction Cosine Similarity

• Hamming distance with Binary Quantization of vectors

• Hamming distance as above with late-interaction re-ranking

The core idea in simple terms in the ColPali paper implementation of late-interaction is:

• We have query embeddings: an array with n vectors, each of size 128 (floats).

• We have document embeddings: an array with 1038 vectors, each of size 128 (floats).

• For each query vector (n), we find the most similar document vector by computing the dot product. Here is simple code for straight-forward dot product similarity.

    import numpy as np
  
    # Define the query vector
    query = np.array([1, 2, 3])
  
    # Define the document vectors
    document_a = np.array([4, 5, 6])
    document_b = np.array([7, 8, 0])
  
    # Compute the dot product between the query and each document
    dot_product_a = np.dot(query, document_a)  # 1*4 + 2*5 + 3*6 = 32
    dot_product_b = np.dot(query, document_b)  # 1*7 + 2*8 + 3*0 = 23
  
    # Output the results
    print(f"Dot product between query and document a: {dot_product_a}")
    print(f"Dot product between query and document b: {dot_product_b}")
    # document a is more similar than document b to our query
  

• Late interaction works like this: take each query vector, find which document vector it matches best with (using dot product), and add up all these best matches. Here's a simple example that shows exactly how this works:

import numpy as np

# One query generates multiple vectors (each vector is 128 floats)
query_vector_1 = np.array([1, 2, 3])  # simplified from 128 floats
query_vector_2 = np.array([0, 1, 1])  # simplified from 128 floats
query = [query_vector_1, query_vector_2]  # one query -> n vectors

# One document generates multiple vectors (each vector is 128 floats)
document_vector_1 = np.array([4, 5, 6])  # simplified from 128 floats
document_vector_2 = np.array([7, 8, 0])  # simplified from 128 floats
document_vector_3 = np.array([1, 1, 1])  # simplified from 128 floats
document = [document_vector_1, document_vector_2, document_vector_3]  # one document -> 1038 vectors

# For each vector in our query, find its maximum dot product with ANY vector in the document
# Then sum these maximums

# First query vector against ALL document vectors
dot_products_vector1 = [
    np.dot(query_vector_1, document_vector_1),  # 1*4 + 2*5 + 3*6 = 32
    np.dot(query_vector_1, document_vector_2),  # 1*7 + 2*8 + 3*0 = 23
    np.dot(query_vector_1, document_vector_3)   # 1*1 + 2*1 + 3*1 = 6
]
max_similarity_vector1 = max(dot_products_vector1)  # 32

# Second query vector against ALL document vectors
dot_products_vector2 = [
    np.dot(query_vector_2, document_vector_1),  # 0*4 + 1*5 + 1*6 = 11
    np.dot(query_vector_2, document_vector_2),  # 0*7 + 1*8 + 1*0 = 8
    np.dot(query_vector_2, document_vector_3)   # 0*1 + 1*1 + 1*1 = 2
]
max_similarity_vector2 = max(dot_products_vector2)  # 11

# Final similarity score is the sum of maximum similarities
final_score = max_similarity_vector1 + max_similarity_vector2  # 32 + 11 = 43

print(f"Final similarity score: {final_score}")

Now - as you can imagine, this is computationally heavy at scale (or so we thought!). So, we looked for ways to see if we can make it faster and maybe even better.

Baseline implementation

To get a realistic picture on real-life performance, we set the parameters as close to our production setup at ColiVara as possible. Embeddings were stored in Postgres with a pgVector extensions. Everything ran in an AWS r6g.xlarge (4 core CPU, 32g ram) and called from our python backend code hosted in a VPS.

We implemented the paper late-interaction calculation as a Postgres function as such:

 CREATE OR replace FUNCTION max_sim(document halfvec[],
                                   query halfvec[]) returns DOUBLE PRECISION
AS
  $$ WITH queries AS
  (
         SELECT row_number() OVER () AS query_number,
                *
         FROM   (
                       SELECT unnest(query) AS query) ), documents AS
  (
         SELECT unnest(document) AS document ), similarities AS
  (
             SELECT     query_number,
                        (document <#> query) * -1 AS similarity
             FROM       queries
             CROSS JOIN documents ), max_similarities AS
  (
           SELECT   max(similarity) AS max_similarity
           FROM     similarities
           GROUP BY query_number )SELECT Sum(max_similarity)
  FROM   max_similarities;

The magic line here is (document <#> query) * -1. The <#> symbol is from pgVector and we multiply with -1 as gives negative inner product by default. We also use halfvecs to store embeddings for efficiency.

Results:

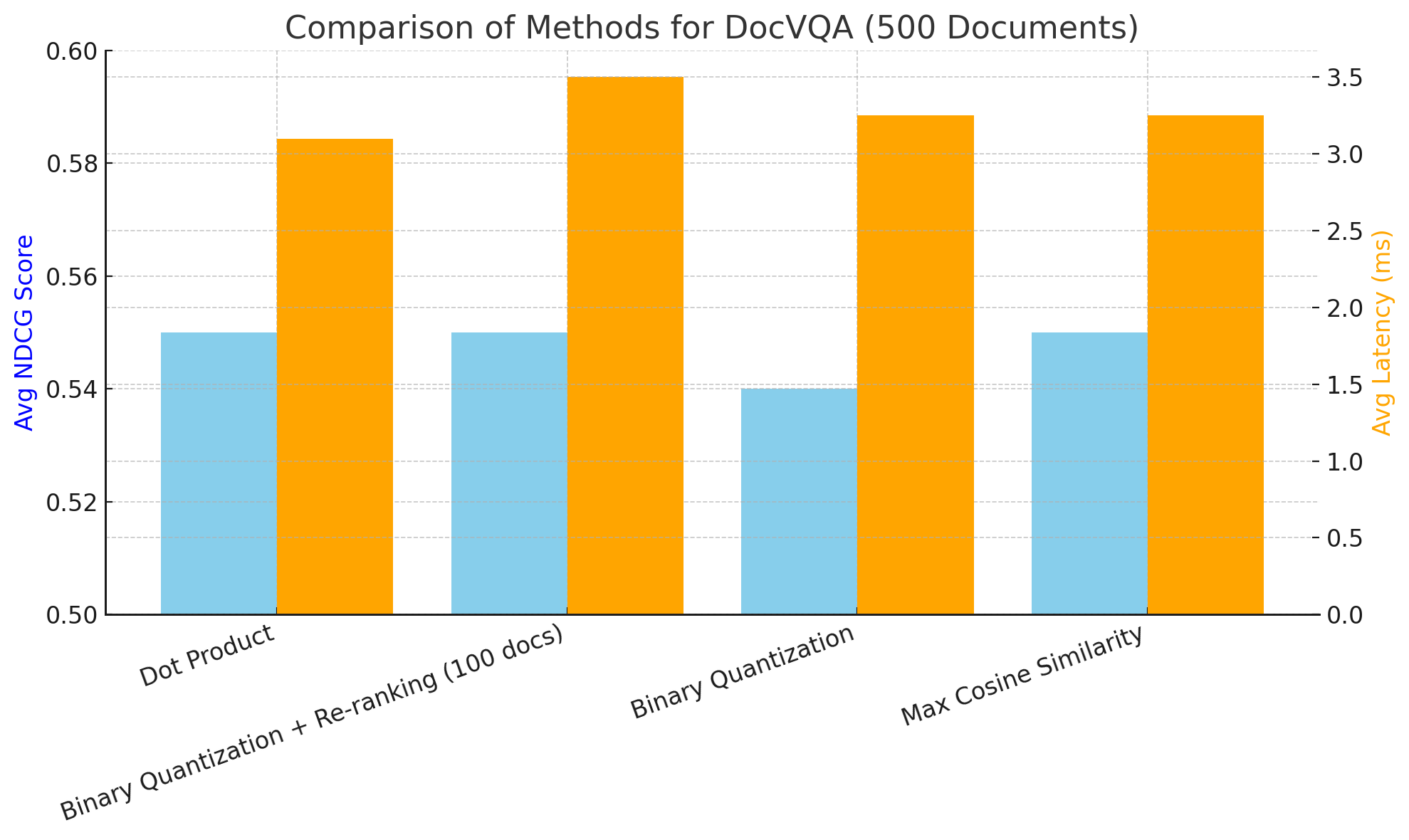
On DocVQA using NCDG@5 and end to end latency we had the following:

• Average NDCG@5 score: 0.55

• Average latency: 3.1 seconds

The dataset is composed of 500 pages.

Late-Interaction Cosine Similarity

Having ran a few large RAG applications before, we were intimately familiar with how cosine similarity works. Cosine similarity normalizes for vector length and gives a few nice additions.

• Values are always between 0 and 1

• This means vectors pointing in the same direction but with different magnitudes will be considered similar

• It is more computationally more expensive than dot product as it needs to calculate vector magnitudes (requires square roots) but also more performant

Our first attempt was meant to establish what would happen if we kept everything the same, but substituted dot product with cosine similarity.

So, we modified our function by replacing the dot product with cosine similarity.

Before:

(document <#> query) * -1 AS similarity

After:

1 - (document <=> query) AS similarity

Then - we ran our evaluations again.

Results:

• Average NDCG@5 score: 0.55

• Average latency: 3.25 seconds

So - our latency went up, but our scores didn’t really improve. It was good to see though that the main latency-driver is not the math behind the calculation. We could use it, and will likely be okay. However, both the latency benefits and the improvements are marginal.

Binary Quantization and Hamming Distance

Binary quantization is a compression technique for vector databases. It converts 32-bit floating point numbers into binary values (1 bit), achieving significant memory savings. The conversion process typically preserves the relative relationships between vectors while sacrificing some precision. For example:

embeddings = [0.123, -0.456, 0.789, -0.012]
quantized_embeddings = [1, 0, 1, 0]

To measure similarity when we have bits as our embeddings, we use the hamming distance. Hamming distance is a measure of the number of differing bits between two binary strings of equal length. It's calculated by comparing the corresponding bits of the two strings and counting the positions at which the bits differ.

First - we converted all our embeddings to be binary and stored them in their own column. Then - we changed our similarity function to be as the pgVector-python documentation recommends.

1 - ((document <~> query) / bit_length(query)

Finally - we ran our evaluations.

Results:

Average NDCG@5 score: 0.54

Average latency: 3.25 seconds

The good news is that the precision loss is minimal. We are hesitant to embrace it fully even with these results, as the loss can be unpredictable. This is essentially a measure of bit diversity, which partly depends on the data being embedded—so your mileage may vary.

The interesting tidbit here is latency is slower, as slow as Cosine similarity. We can almost conclude that if we want to make the process faster, what similarity calculation we should use is probably irrelevant.

Binary Quantization with Re-ranking w/ 100 documents

The final evaluation we wanted to conduct before wrapping up this experiment was to see if we could use Hamming distance and then re-rank using dot product late interactions. If our theory is correct—that the type of similarity calculation doesn't matter much—we should expect a slight increase in latency (since we're doing two calculations) and no significant improvement in performance.

That's exactly what happened.

Results:

• Average NDCG@5 score: 0.55

• Average latency: 3.5 seconds

The bottleneck

Postgres is highly optimized, so adding a square root or doing a bit of extra multiplication has a minimal impact. It's an obvious realization in hindsight, but without conducting evaluations and this experiment, we wouldn't have been able to prove it.The real bottleneck is here:

FROM queries CROSS JOIN documents

the CROSS JOIN is the major bottleneck ! Let's break down the scale:

For each comparison:

• Query: n vectors

• Document: 1038 vectors per page

• Corpus: 500 pages

So for ONE query against ONE page we're doing: n * 1038 vector comparisons (CROSS JOIN)

And for the full 500 pages corpus: n * 1038 * 500 vector comparisons

This creates a massive cartesian product. For example, if n=10 (for query):

• 10,380 comparisons per page

• 5,190,000 comparisons for 500 pages

The CROSS JOIN is creating this quadratic complexity O(n*m) where:

• n = number of query vectors

• m = number of document vectors

So - the math behind the comparisons is relatively inconsequential. The real optimization has to happen before we reach this point.

What can be done?

The crucial optimization insight that we got out of this experiment, is to hyper-focus on the number of pages/documents we are running through our similarity function. Nothing else really matters.

if instead of CROSS JOIN documents (1038 vectors * 500 pages), we first filter:

CROSS JOIN (
    SELECT * FROM documents 
    WHERE page_id IN (
        -- something to pre-filter to maybe 10-20 relevant pages
        -- instead of all 500
    )
)

All of the sudden, we gain massive performance gains. The insight here is for this specific problem: 1038 * 10 pages is so much better than 1038 * 500 pages.

It's like finding a book in a library:

• First narrow to the right section (cheap and quick search)

• Then look for the exact content (expensive vector similarity)

We currently use and recommend advanced filters in ColiVara to reduce the document set. When a user uploads a document, they can add arbitrary JSONs as metadata. It can be very complex or simple. At query time, they can use filtering to reduce the corpus size. This is a powerful technique, but can be complex to setup.

Future work

There is a couple of approaches we planning to tackle to reduce the number of documents without any effort from the user side. The first is a few experiments using Postgres full text search. This will take us away from vision models, but could be straightforward win.

The second is to use vision LLMs generated metadata of documents to store semantic information about the documents automatically at indexing. We can then use existing filtering to reduce the corpus size via that metadata.

The main problem vision models solve in our experience, is that traditional OCR pipelines can’t capture the full visual cues in documents. Here, we don’t want to capture everything, just enough to narrow the search and then vision models will do the rest.

Conclusion

We benchmarked and experimented with several similarity calculations setups for our RAG API using vision models. The differences are marginal and doesn’t meaningfully affect performance or latency.

Due to the large size of embeddings produced, the best performance optimization is to reduce the number of documents that go through the similarity calculation, rather than optimize that similarity calculation itself.