The Ultimate Guide to Complexity Analysis in Data Structures and Algorithms

When you’re trying to fix a problem, there’s usually more than one way to do it. But, how do you pick the best one out of all those choices? To figure this out, let’s check out this article. It gives a comprehensive overview of complexity analysis in data structures and algorithms, aimed at software developers looking to deepen their understanding of this fundamental topic.

What is Complexity Analysis?

Complexity analysis helps us understand how much time or space an algorithm will need as the size of the input grows. The input is our data, and the algorithms are the steps we take to process that data. We estimate the time required to solve a problem or the amount of memory necessary based on our approach.

Asymptotic Notations

There are several types of asymptotic notations, including Big O, Big Omega, and Big Theta. Each notation provides a different perspective on the growth rate of a function.

1. Big-Oh (O) Notation: It represents the maximum amount of time or space required by an algorithm considering all input values. It represents the upper limit of an algorithm’s execution time or space, offering insight into its worst-case complexity.

2. Big-Omega (Ω) notation: It represents the minimum amount of time or space required by an algorithm considering all input values.

3. Big-Theta (Θ) notation: It represents the upper and the lower bound of the running time of an algorithm, it is used for analyzing the average-case complexity of an algorithm.

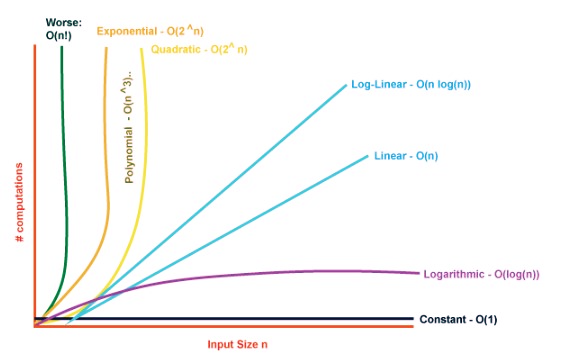
Time Complexity?

Time complexity measures the amount of time an algorithm takes to run as a function of the input size.

Algorithms with lower time complexity are generally more desirable as they can handle larger input sizes with reasonable runtimes. Let’s understand the common time complexities with Java code examples

1. Constant Time: O(1)

The execution time does not depend on the size of the input. No matter how large the input is, the algorithm takes the same amount of time to complete.

public class ConstantTimeExample {
    public static void printFirstElement(int[] array) {
        if (array.length > 0) {
            System.out.println(array[0]);
        }
    }
}

2. Logarithmic Time: O(log n)

The execution time grows logarithmically with the input size.

public class LogarithmicTimeExample {
    public static boolean binarySearch(int[] array, int target) {
        int left = 0;
        int right = array.length - 1;

        while (left <= right) {
            int mid = left + (right - left) / 2;

            if (array[mid] == target) {
                return true;
            }
            if (array[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return false;
    }
}

3. Linear Time: O(n)

The execution time grows linearly with the input size. For each additional element in the input, the algorithm requires a proportional amount of time to process it.

public class LinearTimeExample {
    public static void printAllElements(int[] array) {
        for (int i = 0; i < array.length; i++) {
            System.out.println(array[i]);
        }
    }
}

4. Linearithmic Time: O(n log n)

The algorithm’s runtime grows in proportion to the size of the input multiplied by the logarithm of the input size. Many efficient sorting algorithms, like Merge Sort and Quick Sort, have linearithmic time complexity.

import java.util.Arrays;

public class LinearithmicTimeExample {
    public static void main(String[] args) {
        int[] array = {5, 3, 8, 1, 2};
        Arrays.sort(array); // O(n log n)
        System.out.println(Arrays.toString(array));
    }
}

Arrays.sort uses two sorting algorithms. One is a modification of Quicksort named dual-pivot quicksort, and the other is an adaptation of MergeSort named Timsort. Both have a time complexity of O(n log n), where n is the total number of items in the array.

5. Quadratic Time: O(n²)

The execution time grows quadratically with the input size. This is typical of algorithms with nested loops.

public class QuadraticTimeExample {
    public static void printAllPairs(int[] array) {
        for (int i = 0; i < array.length; i++) {
            for (int j = 0; j < array.length; j++) {
                System.out.println("(" + array[i] + ", " + array[j] + ")");
            }
        }
    }
}

These are the most frequently encountered time complexities. If you’re curious, Please feel free to explore these — Cubic Time (O(n³)), Exponential Time (O(2^n)), and Factorial Time (O(n!)).

Space Complexity?

Space complexity is pretty much a measurement of the total amount of memory that algorithms or operations need to run according to their input size.

Algorithms with lower space complexity are preferred as they optimize memory usage, especially in environments with limited resources. Let’s go through some common space complexities with Java code examples

1. Constant Space: O(1)

The space usage does not depend on the input size.

public class ConstantSpaceExample {  
    public static void printSum(int a, int b) {  
        int sum = a + b; // Constant space  
        System.out.println(sum);  
    }  
}

2. Linear Space: O(n)

The space usage grows linearly with the input size.

public class LinearSpaceExample {  
    public static void createArray(int size) {  
        int[] array = new int[size]; // Linear space  
        for (int i = 0; i < size; i++) {  
            array[i] = i;  
        }  
    }  
}

3. Quadratic Space: O(n²)

public class QuadraticSpaceExample {  
    public static void createMatrix(int size) {  
        int[][] matrix = new int[size][size]; // Quadratic space  
        for (int i = 0; i < size; i++) {  
            for (int j = 0; j < size; j++) {  
                matrix[i][j] = i * j;  
            }  
        }  
    }  
}

Summary

Algorithms with time complexity types such as constant, logarithmic, linear, and linearithmic are typically regarded as the optimal choices for efficient and scalable solutions. Nonetheless, the selection of the most suitable time complexity type varies depending on the specific requirements and constraints of the problem being addressed.

Complexity analysis is a crucial concept for any software developer working with data structures and algorithms. Understanding the complexity of algorithms is crucial for optimizing code and ensuring its efficiency.

Thank you for reading this post. I appreciate your engagement with my content. Feel free to share your thoughts in the comments section. Stay tuned for more updates.