Authors propose Online Personalized Attribute-based Re-ranker (OPAR), a light-weight, within-session personalization approach using multi-arm bandits (MAB). Each arm of the MAB represents an attribute.

As users interact with products, the bandit learns attributes which user is interested in, forming an interpretable user preference profile, which can be used to re-rank products in real-time in a personalized manner.

Complete paper is available at Interpretable Attribute-based Action-aware Bandits for Within-Session Personalization in E-commerce.

Attribute Preference Learning

Initialize attributes with Beta distribution. Different initializations include uniform, random or estimated based on held-out historical datasets.

$$\alpha_{atr} \mathrel{{+}{=}} \delta_{A_t}(1 - e^{-|\mathcal{U_t}|_0})$$

where $\mathcal{U}_t$ denotes the set of attributes existing in items with positive actions (i.e., click, add-to-cart, purchase).

At time step t, for each item user has no action on (say only impression happened), update Beta distribution of associated item attributes as,

$$\beta_{atr} \mathrel{{+}{=}} \delta_{A_t}(1 - e^{-\gamma|\mathcal{V_t}\backslash\mathcal{U_t}|_0})$$

where $\mathcal{V}_t$ is the union of all attributes existing in items user has impressed upon and $\gamma$ controls intensity on implicit no-actions.
User interactions $A_t$ are defined as,

$$A_t(x_i) = \begin{cases} 0, & \text{no action on }x_i\\ 1, & x_i \text{ is purchased}\\ 2, & x_i \text{ is added to cart} \\ 3, & x_i \text{ is clicked} \end{cases}$$

$\delta_{A}$ represent action-aware increments on attribute parameters

Re-Ranking

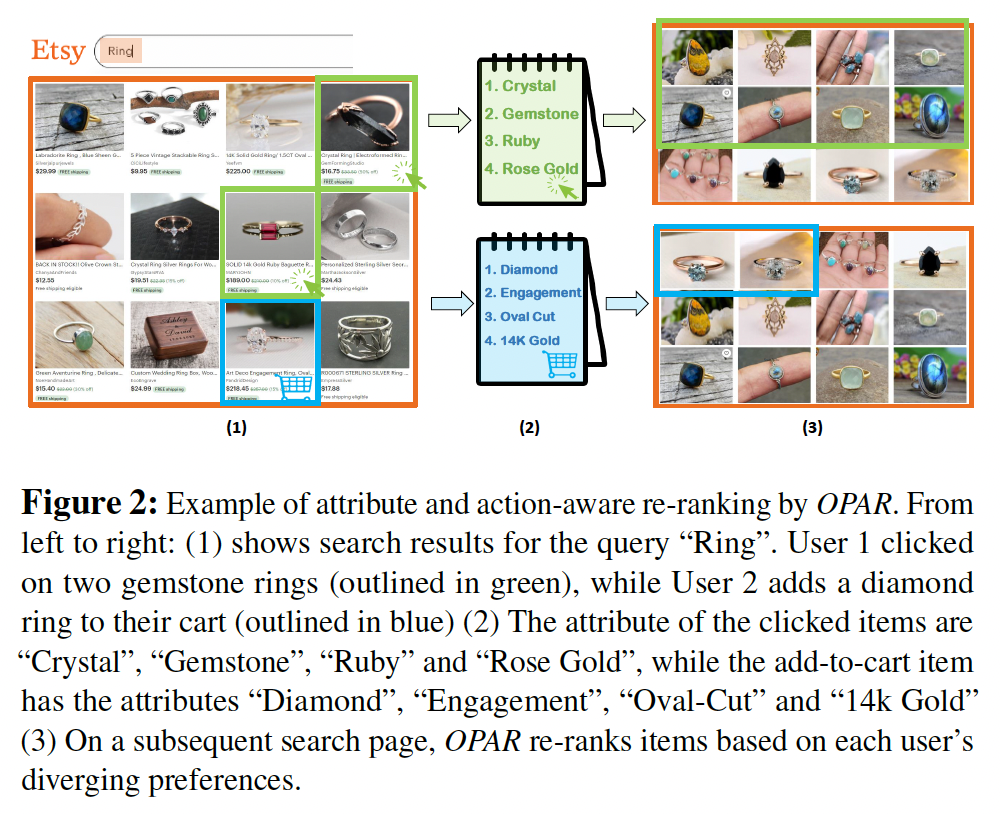
At time step t, for each item user interacted with (say by clicking on a item which has the attribute), update Beta distribution of associated item attributes as,
Sample user preference from the learned distribution of N attributes encountered in the session so far

$$\Theta = \{\theta_{atr_n}\}_{n=1}^N \sim \{Beta(\alpha_{atr_n}, \beta_{atr_n})\}_{n=1}^N$$

Rank the attributes in descending order of preference
For a given item x, sum of reciprocal rank of its attributes represents the item score

$$score(x) = \sum_{atr_h \in x}\frac{1}{rank(\theta_{atr_h})}$$

Re-rank given list based on the derived item scores

OPAR Algorithm

Session

$$S = \{[Q_t, I_t, A_t]\}_{t=1}^T$$

Where at time step t, $Q_t$ is the user query, $I_t$ contains the candidate items to be re-ranked and $A_t$ is the type of user interaction with the items.

Attribute

Each item can be represented by set of its attributes.

$$x_i = \{atr_1, atr_2, ..., atr_{H_x}\}$$

where $H_{x_i}$ denotes the total number of attributes associated with item $x_i$.

$\mathcal{U}_t$ = set of attributes associated from items with positive actions (i.e., click, add-to-cart, purchase), and $\mathcal{V}_t$ be union of all attributes existing in $x_i \in I_y$, i.e.,

$$\begin{align} \mathcal{U}_t &= \cup\{atr_h : \forall atr_h \in x_i\ if\ A_t(x_i) \neq 0,\ \forall x_i \in I_t\} \\ \mathcal{V}_t &= \cup\{atr_h : \forall atr_h \in x_i,\ \forall x_i \in I_t\} \end{align}$$

Now, the complete OPAR algorithm is

Discussion

Assuming all products have similar number of attributes,

For the first set of recommendations, if all attributes are randomly initialized, the re-ranking will be random.
If user interacts with a product whose attributes are not shared by any other product in the recommendation, then only $\alpha$ for corresponding attributes will increase. For all other non-interacted attributes only $\beta$ will increase.
If interacted product attributes are shared by other products also, then both $\alpha$ and $\beta$ will increase for these attributes. For all other non-interacted attributes only $\beta$ will increase.
If user at time step t engages with a lot more attributes then $\alpha$ of corresponding attributes will increase a lot faster than their $\beta$. This intensity of non-action can also be tuned by the hyperparameter $\gamma$.

Interpretable Attribute-based Action-aware Bandits for Within-Session Personalization in E-commerce