Exact Algorithms for the Traveling Salesman Problem: Finding Optimal Solutions
 Lucas Guzzo
Lucas Guzzo
TL;DR
This post explores exact algorithms for solving the Traveling Salesman Problem (TSP), including brute force, dynamic programming (Held-Karp), and branch-and-bound. These methods guarantee the shortest path but come with varying levels of computational expense.
You can find the complete implementations for all algorithms discussed in this series, as well as a simple benchmark tool for running comparisons, in my GitHub repository.
In the world of optimization, finding the exact solution to the Traveling Salesman Problem (TSP) is like discovering the holy grail of route planning. While heuristic and metaheuristic methods can provide approximate solutions quickly, exact algorithms go a step further—they guarantee the shortest possible path, offering unmatched precision.
But precision comes at a cost. Exact algorithms are computationally expensive, especially as the number of cities grows. Despite this, they remain invaluable tools for small to medium-sized problems and for understanding the theoretical underpinnings of TSP.
In this post, we’ll explore three cornerstone exact methods: brute force, dynamic programming (Held-Karp), and branch-and-bound. Each method takes a unique approach to tackle the exponential complexity of TSP, and we’ll break down how they work, where they shine, and their limitations. In the end we will compare them and check when it’s advisable to use each one.
Ready to dive into the world of optimal solutions? Let’s get started!
Brute Force: The Simplest Approach
The brute force method systematically explores all possible routes for the Traveling Salesman Problem (TSP) to guarantee finding the optimal solution. While elegant in its simplicity, it quickly becomes computationally expensive due to factorial growth (O(n-1)!).
To ensure consistency and facilitate comparisons between different algorithms, all solvers in this series implement the same interface:
public interface TspSolver {
int[] solve(int[][] distanceMatrix);
String getName();
}
This interface defines two methods:
solve(int[][] distanceMatrix): Takes a distance matrix as input and returns the optimal route as an array of city indices.getName(): Returns the name of the algorithm for easy identification.
By adhering to this interface, each solver can be swapped in and out seamlessly, allowing for straightforward comparisons of performance, accuracy, and computational efficiency.
The brute force method is implemented as follows:
Step 1: Preparing the List of Cities
First, we need a list of cities (indices) to generate all possible routes. The city at index 0 is treated as the starting point, so we exclude it from the list of cities to permute:
var cities = new int[distanceMatrix.length - 1];
for (int i = 1; i < distanceMatrix.length; i++) {
cities[i - 1] = i;
}
Here:
distanceMatrix.lengthis the total number of cities.We populate the
citiesarray with indices from 1 to (n−1), as city 0 is fixed as the starting and ending point.
Step 2: Generating All Possible Routes
We use recursion to generate all permutations of the cities. The recursive method getRoutes takes the following parameters:
cities: The list of city indices to permute.visited: A boolean array to track which cities have been included in the current route.route: An array to store the current permutation.start: The current depth of recursion.
Here’s how the recursive method works:
private List<int[]> getRoutes(int[] cities, boolean[] visited, int[] route, int start) {
var routes = new ArrayList<int[]>();
// Base case: if the route is complete, add it to the list
if (start == cities.length) {
routes.add(route.clone());
}
// Recursive case: add each unvisited city to the route
for (int i = 0; i < cities.length; i++) {
if (visited[i]) continue;
// Mark the city as visited and add it to the route
route[start] = cities[i];
visited[i] = true;
// Recurse to fill the next position in the route
routes.addAll(getRoutes(cities, visited, route, start + 1));
// Backtrack: unmark the city and reset the route position
route[start] = 0;
visited[i] = false;
}
return routes;
}
Step 3: Evaluating Each Route
Once all routes are generated, we use the DistanceCalculator class to evaluate each route and find the shortest one.
public class DistanceCalculator {
private DistanceCalculator() {}
public static int calculateTotalDistance(int[] route, int[][] distances) {
var totalDistance = 0;
for (int i = 0; i < route.length - 1; i++) {
var city = route[i];
var nextCity = route[i + 1];
totalDistance += distances[city][nextCity];
}
return totalDistance;
}
}
This utility method calculates the total distance for a given route by iterating through the route array and summing the distances between consecutive cities. The final distance is returned.
Here’s how it integrates into the solver.
var bestRoute = new int[cities.length + 2];
var currentRoute = new int[cities.length + 2];
var shortestDistance = Integer.MAX_VALUE;
for (var route : routes) {
// Insert the start and end points (city 0)
System.arraycopy(route, 0, currentRoute, 1, cities.length);
// Calculate the total distance of the route
var routeDistance = DistanceCalculator.calculateTotalDistance(currentRoute, distanceMatrix);
// Update the shortest distance and best route if necessary
if (routeDistance < shortestDistance) {
shortestDistance = routeDistance;
bestRoute = currentRoute.clone();
}
}
Example Walkthrough
Suppose we have 4 cities with the following distance matrix:
| A | B | C | D | |
| A | 0 | 10 | 15 | 20 |
| B | 10 | 0 | 35 | 25 |
| C | 15 | 35 | 0 | 30 |
| D | 20 | 25 | 30 | 0 |
The recursive method generates all possible routes:
- [B, C, D], [B, D, C], [C, B, D], etc.
Each route is evaluated by inserting city A (0) at the start and end:
- A → B → C → D → A = 10 + 35 + 30 + 20 = 95.
The shortest route and its distance are returned.
Strengths and Limitations
Strengths:
Guarantees the shortest route (optimal solution).
Straightforward to understand and implement.
Limitations:
Computationally expensive (O(n-1)!).
Becomes infeasible for larger datasets.
Dynamic Programming: The Held-Karp Algorithm
Dynamic programming is a powerful technique for solving optimization problems by breaking them down into smaller, overlapping subproblems. Instead of solving each subproblem repeatedly, results are stored and reused, significantly reducing redundant computations.
The Held-Karp algorithm applies this principle to the Traveling Salesman Problem (TSP), offering a more efficient alternative to brute force. Although it still has exponential time complexity (O(n²⋅2^n)), it’s far better than the factorial growth of brute force (O(n!)).
The algorithm uses a dynamic programming table to store the shortest paths. Here's how it works:
Define Subproblems:
Let dp[S][i] represent the shortest path to visit all cities in the subset S, ending at city i.
S: A subset of cities (excluding the starting city).
i: The last city in the path.
Base Case:
For the starting city (city 0):
$$dp[\{0\}][0]=0$$
This means the cost to start at city 0 is 0.
Recursive Relation:
For each subset S containing city i, calculate:
$$dp[S][i] = \min_{j \in S, j \neq i} \left( dp[S \setminus \{i\}][j] + \text{dist}[j][i] \right)$$
This means the shortest path to i is the minimum cost of visiting a city j in subset S (excluding i), plus the cost of traveling from j to i.
Final Step:
After filling the table, calculate the shortest path that returns to the starting city:
$$\text{cost} = \min_{i \neq 0} \left( dp[\{1, 2, \dots, n-1\}][i] + \text{dist}[i][0] \right)$$
Example Walkthrough
Suppose we have the same scenario from the example solved with Brute Force.
Step 1: Initialization
We start by defining the dynamic programming table dp[S][i]
Initially:
$$dp[\{0\}][0]=0$$
This means the cost of starting at city A (city 0) is 0.
All other entries in the table are initialized to infinity (∞), as they represent uncomputed or invalid states.
Step 2: Building the Table
We compute the values of dp[S][i] iteratively for all subsets S of increasing size. Let’s break it down:
Subset S={0,1} ending at B (city 1):
$$dp[\{0,1\}][1]=dp[\{0\}][0] + dist[0][1]$$
Substituting values:
$$dp[\{0,1\}][1]=0+10=10$$
Subset S={0,2} ending at C (city 2):
$$dp[\{0,2\}][2]=dp[\{0\}][0] + dist[0][2]$$
Substituting values:
$$dp[\{0,2\}][2]=0 + 15=15$$
Subset S={0,3} ending at D (city 3):
$$dp[\{0,3\}][3] = dp[\{0\}][0]+dist[0][3]$$
Substituting values:
$$dp[\{0,3\}][3] = 0 + 20=20$$
Step 3: Expanding Subsets
We now compute for larger subsets, such as S={0,1,2} and S = {0,1,2,3}.
Subset S={0,1,2} ending at C (city 2):
$$dp[\{0,1,2\}][2]=min(dp[\{0,1\}][1]+dist[1][2])$$
Substituting values:
$$dp[\{0,1,2\}][2] = min(10 + 35) = 45$$
Applying to the all subsets of this same size, we have:
dp[{0,1,2}][1]=50
dp[{0,1,2}][2]=45
dp[{0,1,3}][1]=45
dp[{0,1,3}][3]=35
dp[{0,2,3}][2]=50
dp[{0,2,3}][3]=45
Subset S={0,1,2,3} ending at D (city 3):
$$dp[\{0,1,2,3\}][3]=min(dp[\{0,1,2\}][1]+dist[1][3],dp[\{0,1,2\}][2]+dist[2][3])$$
Substituting values:
$$dp[\{0,1,2,3\}][3]=min(50+35,45+30)=min(85,75)=75$$
Applying to the all subsets of this same size, we have:
dp[{0,1,2,3}][1]=70
dp[{0,1,2,3}][2]=65
dp[{0,1,2,3}][3]=75
Step 4: Final Step
After filling all entries in the table, compute the minimum cost of completing the cycle
$$\text{cost} = \min_{i \neq 0} \left( dp[\{0,1,2,3\}][i] + \text{dist}[i][0] \right)$$
Substituting values:
$$\text{cost} = \min_{i \neq 0} \left( dp[\{0,1,2,3\}][1] + \text{dist}[1][0],\{0,1,2,3\}][2] + \text{dist}[2][0],\{0,1,2,3\}][3] + \text{dist}[3][0] \right)$$
$$\text{cost} = \min_{i \neq 0} \left( 70 + 10, 65+15, 75+20 \right)=min(80,80,95)=80$$
Step 5: Reconstruct the shortest route:
The minimum cost is 80 and it occurs when the route ends either at B (city 1) or C (city 2). Reconstructing the route back from the dynamic programming table, we have the two optimal routes.
A → C → D→ B → A
A → B → D → C → A
Implementation
Now that we know how this method works, let’s begin implementing our new solver. We’ll start by initializing the needed variables.
var n = distanceMatrix.length; // Number of cities
var dp = new int[1 << n][n]; // The dynamic programming table
var parent = new int[1 << n][n]; // Stores the optimal end city from previous subsets
You might have noticed we initialized the matrix with size 1 << n. For those not familiarized, 1 << n is a bitwise operation that computes 2^n, representing the total number of subsets of n cities. Here’s how it works:
Bitmasking: We use an integer's binary representation to encode subsets of cities. Each bit in the integer corresponds to whether a particular city is included in the subset:
Bit 0: Represents city 0 (A).
Bit 1: Represents city 1 (B).
Bit 2: Represents city 2 (C), and so on.
Example for n=4:
1<<4=16, meaning there are 2^4 = 16 subsets of cities.
Each subset is represented by a binary number:
0001: Subset {0}, only city A.
0101: Subset {0,2}, cities A and C.
1111: Subset {0,1,2,3}, all cities.
Bitmasking uses bitwise operations to efficiently manipulate and check subsets:
Checking if a City is in the Subset:
mask & (1 << city)checks whether the bit corresponding tocityis set to 1 inmask.Example: If
mask = 5(0101):mask & (1 << 2)→ 0101 & 0100 = 0100 ≠ 0, so city 2 is in the subset.mask & (1 << 1)→ 0101 & 0010 = 0000 = 0, so city 1 is not in the subset.
Adding a City to the Subset:
mask | (1 << city)sets the bit corresponding tocityto 1.Example: Add city 1 to
mask = 5(0101):- 0101 | 0010 = 0111, so the new subset is {0,1,2}.
Removing a City from the Subset:
mask ^ (1 << city)toggles the bit corresponding tocity.Example: Remove city 2 from
mask = 5(0101):- 0101 ^ 0100 = 0001, so the new subset is {0}.
Using bitmasking for representing the subsets gives us efficiency (check, add and remove lements is O(1)) and a compact representation, requiring only O(n) bits for each subset.
Back to our implementation, now we initialize our DP table, setting all entries to infinity. This ensures that only valid transitions update the table. If a state is never computed, it remains at infinity.
for (var i = 0; i < (1 << n); i++) {
Arrays.fill(dp[i], Integer.MAX_VALUE);
}
dp[1][0] = 0;
We also set our base case, with a cost of 0, as there are no cost associated with starting at the starting city. City A (city 0) is represented by subset 1 (0001), a subset containing only this city.
Now we need to populate the DP table with the corrects costs for each route. We do this by iterating over all subset of cities.
for (int mask = 1; mask < (1 << n); mask++) {
if ((mask & 1) == 0) continue; // Ensure city 0 is always in the subset
for every subset we to iterate over all its potential final cities. We check if a city is in the subset by doing mask & 1 << city.
for (var city = 1; city < n; city++) {
if ((mask & 1 << city) == 0) continue; // Skip if city is not in the subset
Now, to calculate the cost of this route, we need to get the current subset without the current city. We do this with mask ^ (1 << city). Then we compute its cost plus the distance to current city, fo every possible ending city in that subset. The minimum value will be the cost for the current subset ending in the current city.
int prevMask = mask ^ (1 << city);
for (var lastCity = 0; lastCity < n; lastCity++) {
if ((prevMask & 1 << lastCity) == 0) continue; // Skip if lastCity is not in prevMask
var distance = dp[prevMask][lastCity] == Integer.MAX_VALUE ?
Integer.MAX_VALUE :
dp[prevMask][lastCity] + distanceMatrix[lastCity][city];
if (distance < dp[mask][city]) {
dp[mask][city] = distance;
parent[mask][city] = lastCity;
}
Notice that we are storing the last city used for this route in the parent matrix. We will use that in the future when reconstructing the best route.
To find the best route, we get the subset that includes all cities and calculate its final cost, meaning the cost to end in every possible city plus the distance from that city to city A.
int mask = (1 << n) - 1; // All cities included
int lastCity = 0;
int shortestDistance = Integer.MAX_VALUE;
for (int i = 1; i < n; i++) {
int routeCost = dp[mask][i] + distanceMatrix[i][0];
if (routeCost < shortestDistance) {
shortestDistance = routeCost;
lastCity = i;
}
}
Knowing the best route, and the city where it ends, we can start reconstructing the complete path.
int[] bestRoute = new int[n + 1];
for (int i = n - 1; i > 0; i--) {
bestRoute[i] = lastCity;
lastCity = parent[mask][lastCity];
mask ^= (1 << bestRoute[i]); // Remove lastCity from the subset
}
This is how the final implementation should look like.
public class HeldKarpSolver implements TspSolver {
@Override
public String getName() {
return "Held-Karp";
}
@Override
public int[] solve(int[][] distanceMatrix) {
var n = distanceMatrix.length; // Number of cities
var dp = new int[1 << n][n]; // The dynamic programming table
var parent = new int[1 << n][n]; // Stores the optimal end city from previous subsets
// Initialize DP table with infinity
for (var i = 0; i < (1 << n); i++) {
Arrays.fill(dp[i], Integer.MAX_VALUE);
}
// Base case: city 0 is the starting point and the total distance of this subset is 0.
dp[1][0] = 0;
// Iterate over all subsets of cities, where mask is the bitmask of the subset
for (int mask = 1; mask < (1 << n); mask++) {
// Since we always start from city 0, we only consider subsets where it is present.
if ((mask & 1) == 0) continue;
// Iterate over all possible final cities from this subset to calculate subset distances
// Since city 0 will never be the final city of the subset, we start fromm city 1
for (var city = 1; city < n; city++) {
// Check if city is in subset
if ((mask & 1 << city) == 0) continue;
// Gets a subset of the current subset where the current city is not present
int prevMask = mask ^ (1 << city);
// Iterate over all possible final cities from previous subset to find the best final city
// Since previous subset could also be just the city 0, we start this iteration from 0
for (var lastCity = 0; lastCity < n; lastCity++) {
if ((prevMask & 1 << lastCity) == 0) continue;
var distance = dp[prevMask][lastCity] == Integer.MAX_VALUE ?
Integer.MAX_VALUE :
dp[prevMask][lastCity] + distanceMatrix[lastCity][city];
if (distance < dp[mask][city]){
dp[mask][city] = distance;
parent[mask][city] = lastCity;
}
}
}
}
// Find the minimum cost of returning to the starting city
int mask = (1 << n) - 1;
int lastCity = 0;
int shortestDistance = Integer.MAX_VALUE;
for (int i = 1; i < n; i++) {
int routeCost = dp[mask][i] + distanceMatrix[i][0];
if (routeCost < shortestDistance) {
shortestDistance = routeCost;
lastCity = i;
}
}
// Reconstruct the path moving backwards
int[] bestRoute = new int[n + 1];
for (int i = n - 1; i > 0; i--) {
bestRoute[i] = lastCity;
lastCity = parent[mask][lastCity];
// After adding last city to the route, we get the subset where it is missing
mask ^= (1 << bestRoute[i]);
}
return bestRoute;
}
}
Strengths and Limitations
Strengths
Guarantees Optimality:
Like brute force, the Held-Karp algorithm ensures the shortest possible route is found. It’s a powerful method for solving small to medium-sized Traveling Salesman Problem (TSP) instances.Improved Efficiency Over Brute Force:
While brute force has O(n!) time complexity, Held-Karp reduces this to O(n²⋅2^n), which is significantly faster for larger m.Scales Better for Medium-Sized Problems:
Practical for n≤20~30, depending on available memory and computational resources.
Limitations
Exponential Time Complexity:
Despite being more efficient than brute force, Held-Karp still has exponential growth in runtime due to the 2^n subsets. This makes it impractical for n>30 in most cases.High Memory Usage:
The O(n²⋅2^n) space complexity requires storing results for all subsets of cities and possible end cities. Memory usage grows exponentially as n increases.Implementation Complexity:
Compared to brute force, Held-Karp is more challenging to implement due to its reliance on bitmasking and dynamic programming.
Branch and Bound: A Smarter Brute Force
The Branch and Bound (B&B) method is an optimization algorithm that builds on brute force by significantly reducing the number of paths explored. It does this by:
Branching: Systematically dividing the problem into smaller subproblems (branches).
Bounding: Calculating an optimistic lower bound for each branch to determine if it’s worth exploring further.
If the lower bound of a branch exceeds the current best solution, that branch is pruned (skipped), saving computation time.
How It Works
Initial Setup:
Start with all cities and consider the initial city (e.g., A) as the root node of a search tree. Each branch represents a potential route to explore.Branching:
At each level of the tree, add one city to the current path, generating new branches. Continue branching until a complete tour is formed.Bounding:
For each branch, calculate a lower bound on the possible total cost of completing the tour. The lower bound is an estimate of the minimum possible cost, considering the current partial path and the best-case scenario for the remaining cities.Pruning:
If the lower bound of a branch is greater than or equal to the cost of the current best solution, discard that branch. Otherwise, explore it further.Complete and Compare:
When a complete tour is found, compare its cost to the current best solution. Update the best solution if the new tour has a lower cost.
Why It’s Better than Brute Force
Brute Force explores all possible routes exhaustively, while Branch and Bound prunes unnecessary branches early.
For nnn cities, brute force evaluates n!n!n! routes, whereas B&B evaluates only a subset of promising routes, reducing computational effort significantly.
Example Walkthrough
Let’s use the same example we used for the other methods.
Root Node:
Start at city A (0). The lower bound is calculated based on the minimum outgoing edges for all cities:From A: Min(10, 15, 20) = 10.
From B: Min(10, 25, 35) = 10.
From C: Min(15, 30, 35) = 15.
From D: Min(20, 25, 30) = 20.
Total lower bound:
$$\frac{10 + 10 + 15 + 20}{2} = 27.5$$
Branching begins by selecting the next city to visit.
First Branch:
A → B. The new lower bound is calculated based on the remaining cities (C, D). If the lower bound is higher than the current best solution, this branch is pruned.Continue Branching:
Evaluate branches like A → B → C and A → B → D, calculating lower bounds for each. Prune branches as necessary.Completion:
Once a complete tour is found (e.g., A → B → C → D → A), compare its cost to the current best solution and update if it’s better.
Implementation
Now let’s implement our new Branch & Bound solver. As always, we begin initializing the main variable we’ll be using throught the method.
var route = new int[distanceMatrix.length + 1];
var bestRoute = new int[distanceMatrix.length + 1];
var visited = new boolean[distanceMatrix.length];
var cities = new int[distanceMatrix.length];
for (int i = 0; i < distanceMatrix.length; i++) {
cities[i] = i;
}
Now to thet actuallogic. This method is a modification of the Brute Force methd and you will notice some similarities. The difference relies in the fact that we calculate the route cost while we create the route and compare it with the the best value we’ve got so far. If it’s not smalles than the best value, then we move on to the next iteration.
if (level == cities.length) {
int totalCost = currentCost + distanceMatrix[currentCity][0];
if (totalCost < minCost.get()) {
minCost.set(totalCost);
System.arraycopy(currentPath, 0, bestRoute, 0, cities.length);
}
return;
}
We also perform this check earlier in the permutation, using the lower bound technique.
for (var nextCity = 0; nextCity < cities.length; nextCity++) {
if (!visited[nextCity]) {
var newCost = currentCost + distanceMatrix[currentCity][nextCity];
var lowerBound = getBound(nextCity, cities, visited, distanceMatrix);
// Prune if the new lower bound is not promising
if (newCost + lowerBound < minCost.get()) {
visited[nextCity] = true;
currentPath[level] = nextCity;
branchAndBound(nextCity, newCost, level + 1, currentPath, cities, visited, distanceMatrix, minCost, bestRoute);
visited[nextCity] = false; // Backtrack
currentPath[level] = 0;
}
}
}
The lower bound is calculated with the help of two auxiliar methods.
private double getBound(int candidateCity, int[] cities, boolean[] visited, int[][] distanceMatrix) {
return (double) Arrays.stream(cities)
.filter(x -> !visited[x])
.map(x -> getMinEdgeCost(x, candidateCity, visited, distanceMatrix))
.sum() / 2;
}
private int getMinEdgeCost(int city, int candidateCity, boolean[] visited, int[][] distanceMatrix) {
var cost = IntStream.range(0, distanceMatrix.length)
.filter(i -> i != city && (!visited[i] || i == 0) && i != candidateCity)
.map(x -> distanceMatrix[city][x])
.min();
return cost.isPresent() ? cost.getAsInt() : 0;
}
The finalimplementation should look like this.
public class BranchAndBoundSolver implements TspSolver {
@Override
public String getName() {
return "BranchAndBound";
}
@Override
public int[] solve(int[][] distanceMatrix) {
var cities = new int[distanceMatrix.length];
for (int i = 0; i < distanceMatrix.length; i++) {
cities[i] = i;
}
var route = new int[distanceMatrix.length + 1];
var bestRoute = new int[distanceMatrix.length + 1];
var visited = new boolean[distanceMatrix.length];
visited[0] = true;
branchAndBound(
0,
0,
1,
route,
cities,
visited,
distanceMatrix,
new AtomicInteger(Integer.MAX_VALUE),
bestRoute);
return bestRoute;
}
private void branchAndBound(
int currentCity,
int currentCost,
int level,
int[] currentPath,
int[] cities,
boolean[] visited,
int[][] distanceMatrix,
AtomicInteger minCost,
int[] bestRoute) {
if (level == cities.length) {
// Complete the cycle back to the starting city
int totalCost = currentCost + distanceMatrix[currentCity][0];
if (totalCost < minCost.get()) {
minCost.set(totalCost);
System.arraycopy(currentPath, 0, bestRoute, 0, cities.length);
}
return;
}
for (var nextCity = 0; nextCity < cities.length; nextCity++) {
if (!visited[nextCity]) {
var newCost = currentCost + distanceMatrix[currentCity][nextCity];
var lowerBound = getBound(nextCity, cities, visited, distanceMatrix);
// Prune if the new lower bound is not promising
if (newCost + lowerBound < minCost.get()) {
visited[nextCity] = true;
currentPath[level] = nextCity;
branchAndBound(nextCity, newCost, level + 1, currentPath, cities, visited, distanceMatrix, minCost, bestRoute);
visited[nextCity] = false; // Backtrack
currentPath[level] = 0;
}
}
}
}
private double getBound(int candidateCity, int[] cities, boolean[] visited, int[][] distanceMatrix) {
return (double) Arrays.stream(cities).filter(x -> !visited[x]).map(x -> getMinEdgeCost(x, candidateCity, visited, distanceMatrix)).sum() / 2;
}
private int getMinEdgeCost(int city, int candidateCity, boolean[] visited, int[][] distanceMatrix){
var cost = IntStream.range(0, distanceMatrix.length)
.filter(i -> i != city && (!visited[i] || i == 0) && i != candidateCity)
.map(x -> distanceMatrix[city][x])
.min();
return cost.isPresent() ? cost.getAsInt() : 0;
}
Strengths of Branch and Bound
Guaranteed Optimality:
Like brute force, Branch and Bound finds the exact optimal solution for the Traveling Salesman Problem (TSP), making it a reliable choice when accuracy is critical.Effective Pruning:
By leveraging lower bounds to prune unpromising branches, B&B significantly reduces the number of paths explored compared to brute force.Flexibility in Lower Bound Heuristics:
The algorithm allows for the use of different lower-bound techniques (e.g., reduced cost matrix, minimum spanning tree) to improve pruning efficiency.Adaptable for Variants of TSP:
Branch and Bound can be easily adapted to handle constraints like time windows, precedence relationships, or asymmetric costs.Systematic Search:
The algorithm explores solutions in a structured way, ensuring all possibilities are accounted for without unnecessary repetition.
Limitations
Exponential Time Complexity in the Worst Case:
While pruning improves performance, the worst-case time complexity remains exponential (O(n!)) if most branches need to be explored.Dependence on Lower Bound Quality:
The efficiency of B&B heavily relies on the tightness of the lower bound. Poor lower bounds result in fewer pruned branches and increased runtime.Memory Usage:
Recursive implementations require additional memory for storing the search tree, current paths, visited states, and best solutions.Scalability:
B&B is impractical for large TSP instances (e.g., n>30) because the number of branches grows exponentially with the number of cities.Computational Overhead for Lower Bound Calculation:
Techniques like the reduced cost matrix or minimum spanning tree add computational overhead to each node evaluation, which may negate pruning gains in smaller problems.
Conclusion: Comparing Exact Methods for the Traveling Salesman Problem
In this post, we’ve explored three exact methods for solving the Traveling Salesman Problem (TSP): Brute Force, Held-Karp, and Branch and Bound. Each method guarantees an optimal solution but differs significantly in terms of performance, scalability, and practicality. Let’s summarize their strengths, limitations, and real-world applicability.
Brute Force: The Simplest Approach
Brute force explores every possible route (n!) to find the optimal solution. While easy to understand and implement, its exponential growth in computational time makes it impractical for more than 10 cities. For small problems, however, brute force may still be a viable option due to its simplicity.
Held-Karp: The Dynamic Programming Powerhouse
The Held-Karp algorithm improves on brute force with a time complexity of O(n²⋅2^n), reducing redundant calculations by leveraging dynamic programming. This method consistently outperforms both brute force and Branch and Bound for medium and large problem sizes, as evidenced by benchmark results.
From the chart, we see that Held-Karp scales much better than Branch and Bound for problems with more than 10-15 cities. Despite its high memory requirements, Held-Karp is the most practical exact method for problems with up to 20-25 cities.
Branch and Bound: Smart Pruning, Limited Scalability
Branch and Bound employs smart pruning to avoid evaluating unpromising routes. While it often outperforms brute force in small to medium-sized problems, its factorial complexity in worst-case scenarios limits its scalability. The effectiveness of this method depends heavily on the quality of the lower-bound heuristic, and as problem size increases, Held-Karp emerges as the better choice for exact solutions.
Choosing the Right Method
Based on the benchmarks and theoretical insights, here’s when to use each method:
Brute Force: For very small problems (n≤10) where simplicity matters more than performance.
Held-Karp: For medium to larger problems (n≤25) where memory constraints are manageable.
Branch and Bound: For small to medium problems (n≤15) where a good lower-bound heuristic is available.
Final Thoughts
The chart below illustrates the performance of these methods as the number of cities increases. While Branch and Bound provides significant improvements over brute force for smaller inputs, Held-Karp consistently delivers better performance as problem size grows, solidifying its position as the most efficient exact algorithm for solving TSP.
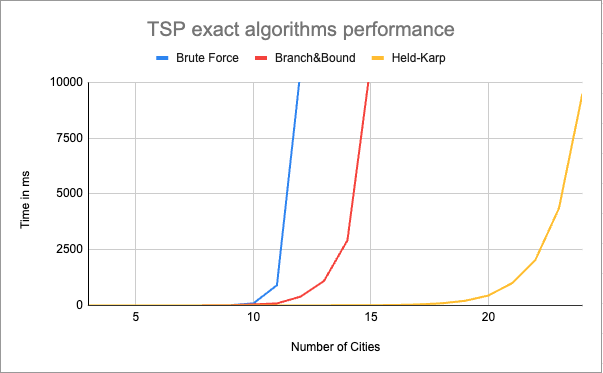
When the number of cities exceeds 20-25, even Held-Karp becomes computationally expensive. At this point, approximate methods like Genetic Algorithms, Simulated Annealing, or Ant Colony Optimization are better alternatives.
By understanding the trade-offs of each method, you can make informed decisions about which approach to use based on your problem size and computational resources.
Subscribe to my newsletter
Read articles from Lucas Guzzo directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
