My Week with Graph Theory: Part 1

Introduction to Graph Theory: A Personal Learning Journey

When I first started, graphs seemed overwhelming. While I was familiar with trees from data structures, graphs felt more complex. I began by understanding the basics: nodes, edges, directed and undirected graphs, and how they model real-world relationships.

We should not memorize the algorithm itself, but rather the idea and some implementation notes. Under each algorithm, I’ve included notes that can help remember the algorithm. Knowing the high-level implementation will be pivotal to gaining confidence in our knowledge and skill set.

What is Graph Theory?

Graph theory studies mathematical structures modeling pairwise relationships. A graph consists of:

• Vertices (Nodes): Entities like people or intersections.

• Edges: Connections between vertices, which can be directed or undirected, and may have weights.

Key Graph Algorithms Implemented

Depth-First Search (DFS)

• Definition: An algorithm for traversing or searching tree or graph data structures.

How DFS Works

1. Starts at the root node (or an arbitrary node for a graph).

2. Explores as far as possible along each branch before backtracking.

Example Implementation in Java:

import java.util.*;

public class DFS {
    private int V;
    private LinkedList<Integer> adj[];

    DFS(int v) {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }

    void addEdge(int v, int w) {
        adj[v].add(w);
    }

    void DFSUtil(int v, boolean visited[]) {
        visited[v] = true;
        System.out.print(v + " ");

        for (int n : adj[v]) {
            if (!visited[n])
                DFSUtil(n, visited);
        }
    }

    void DFS(int v) {
        boolean visited[] = new boolean[V];
        DFSUtil(v, visited);
    }
}

Notes on DFS

• Recursion: DFS typically uses recursion for implementation.

• Mark Visited: A node is marked as visited, and its neighbors are explored if not yet visited.

Applications of DFS

• Finding connected components:

  • Iterate through all nodes.

  • Call dfs() to find all nodes belonging to a particular component.

DFS Visualization

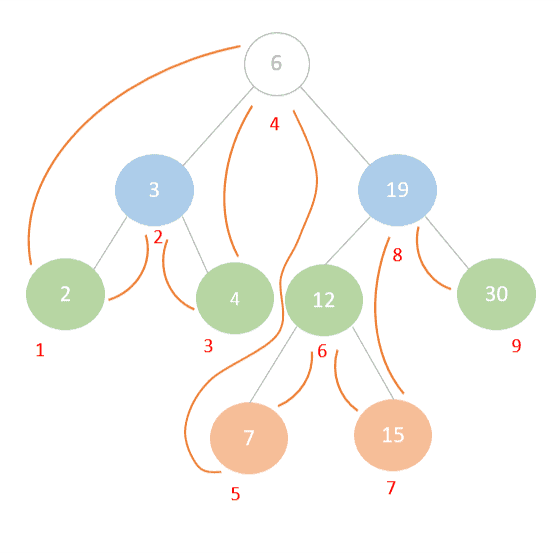
Breadth-First Search (BFS)

• Definition: An algorithm for searching tree data structures for a node that satisfies a given property.

• Approach: Explores all nodes at the current depth before moving to the next level.

Example Implementation in Java:

import java.util.*;

public class BFS {
    private int V;
    private LinkedList<Integer> adj[];

    BFS(int v) {
        V = v;
        adj = new LinkedList[v];
        for (int i = 0; i < v; ++i)
            adj[i] = new LinkedList();
    }

    void addEdge(int v, int w) {
        adj[v].add(w);
    }

    void BFS(int s) {
        boolean visited[] = new boolean[V];
        LinkedList<Integer> queue = new LinkedList<>();

        visited[s] = true;
        queue.add(s);

        while (queue.size() != 0) {
            s = queue.poll();
            System.out.print(s + " ");

            for (int n : adj[s]) {
                if (!visited[n]) {
                    visited[n] = true;
                    queue.add(n);
                }
            }
        }
    }
}

BFS Key Notes

• Graph Representation:

  • Uses an adjacency list (LinkedList[]) to store edges for each vertex.

• Add Edge:

  • addEdge(v, w) adds an edge from vertex v to vertex w.

• Time Complexity:

  • O(V + E): Every vertex and edge is processed once.

• Space Complexity:

  • O(V): For the visited array and the queue.

BFS Visualization

Dijkstra's Algorithm: Finding the Shortest Path

• Purpose: Finds the shortest paths between nodes in a graph, often used in scenarios like road networks.

Example Implementation in Java:

import java.util.*;

public class Dijkstra {
    static class Node {
        int id;
        int cost;

        Node(int id, int cost) {
            this.id = id;
            this.cost = cost;
        }
    }

    public static int dijkstra(int start, int end, Map<Integer, List<Node>> graph, int n) {
        int[] dist = new int[n + 1];
        Arrays.fill(dist, Integer.MAX_VALUE);
        dist[start] = 0;

        PriorityQueue<Node> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a.cost));
        pq.offer(new Node(start, 0));

        Set<Integer> visited = new HashSet<>();

        while (!pq.isEmpty()) {
            Node current = pq.poll();
            int node = current.id;
            int cost = current.cost;

            if (visited.contains(node)) continue;
            visited.add(node);

            if (node == end) return cost;

            for (Node neighbor : graph.get(node)) {
                int newCost = cost + neighbor.cost;
                if (newCost < dist[neighbor.id]) {
                    dist[neighbor.id] = newCost;
                    pq.offer(new Node(neighbor.id, newCost));
                }
            }
        }

        return dist[end] == Integer.MAX_VALUE ? -1 : dist[end];
    }

    public static void main(String[] args) {
        Map<Integer, List<Node>> graph = new HashMap<>();
        graph.put(1, Arrays.asList(new Node(2, 1), new Node(3, 4)));
        graph.put(2, Arrays.asList(new Node(3, 2), new Node(4, 5)));
        graph.put(3, Arrays.asList(new Node(4, 1)));
        graph.put(4, Arrays.asList());

        int start = 1, end = 4;
        int result = dijkstra(start, end, graph, 4);

        System.out.println("Shortest path from " + start + " to " + end + ": " + result);
    }
}

Key Notes on Dijkstra's Algorithm

• Priority Queue:

  • Retrieves the node with the smallest distance for processing.

• Optimization:

  • Skip nodes where a shorter path has already been found.

• Time Complexity:

  • O((V + E) log V): Efficient for graphs with weighted edges.

Dijkstra's Visualization

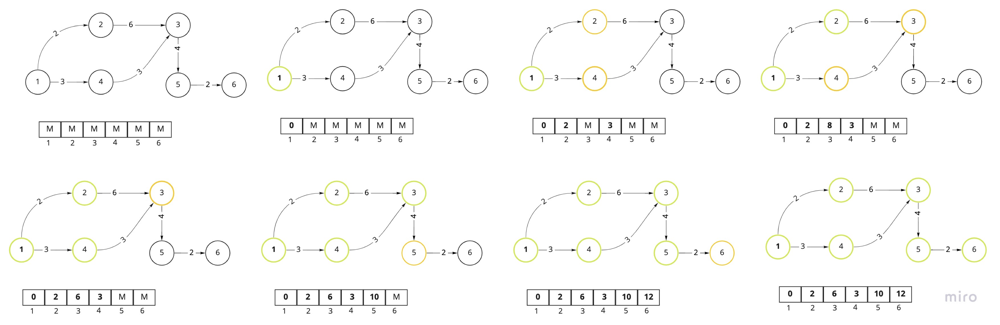
Union-Find Algorithm: Managing Disjoint Sets

• Definition: A data structure that stores a collection of disjoint sets (non-overlapping groups) and supports efficient merging and finding operations.

Key Operations

1. Find: Determines which subset a particular element is in.

2. Union: Joins two subsets into a single subset.

Example Implementation in Java:

import java.util.*;

public class DisjointSet {
    private final List<Integer> rank;
    private final List<Integer> parent;

    public DisjointSet(int n) {
        rank = new ArrayList<>();
        parent = new ArrayList<>();
        for (int i = 0; i <= n; i++) {
            rank.add(0);
            parent.add(i);
        }
    }

    private int findParent(int node) {
        if (node == parent.get(node)) {
            return node;
        }
        int ulp = findParent(parent.get(node));
        parent.set(node, ulp);
        return parent.get(node);
    }

    public void unionByRank(int u, int v) {
        int ulp_u = findParent(u);
        int ulp_v = findParent(v);
        if (ulp_u == ulp_v) return;
        if (rank.get(ulp_u) > rank.get(ulp_v)) {
            parent.set(ulp_v, ulp_u);
        } else if (rank.get(ulp_u) < rank.get(ulp_v)) {
            parent.set(ulp_u, ulp_v);
        } else {
            parent.set(ulp_v, ulp_u);
            int rank_u = rank.get(ulp_u);
            rank.set(ulp_u, rank_u + 1);
        }
    }

    public boolean isSameComponent(int u, int v) {
        return findParent(u) == findParent(v);
    }
}

class Main {
    public static void main(String[] args) {
        DisjointSet set = new DisjointSet(7);

        set.unionByRank(1, 2);
        set.unionByRank(2, 3);
        set.unionByRank(4, 5);
        set.unionByRank(5, 6);
        set.unionByRank(6, 7);

        System.out.println("Are 2 and 7 in the same component? " + set.isSameComponent(2, 7)); // false
        set.unionByRank(3, 7);
        System.out.println("Are 2 and 7 in the same component? " + set.isSameComponent(2, 7)); // true
    }
}

Notes on Union-Find

• Path Compression: Optimizes find operations by ensuring each node points directly to its root.

• Union by Rank: Merges smaller trees under larger ones to maintain efficiency.

• Applications:

  • Network connectivity.

  • Finding connected components in a graph.

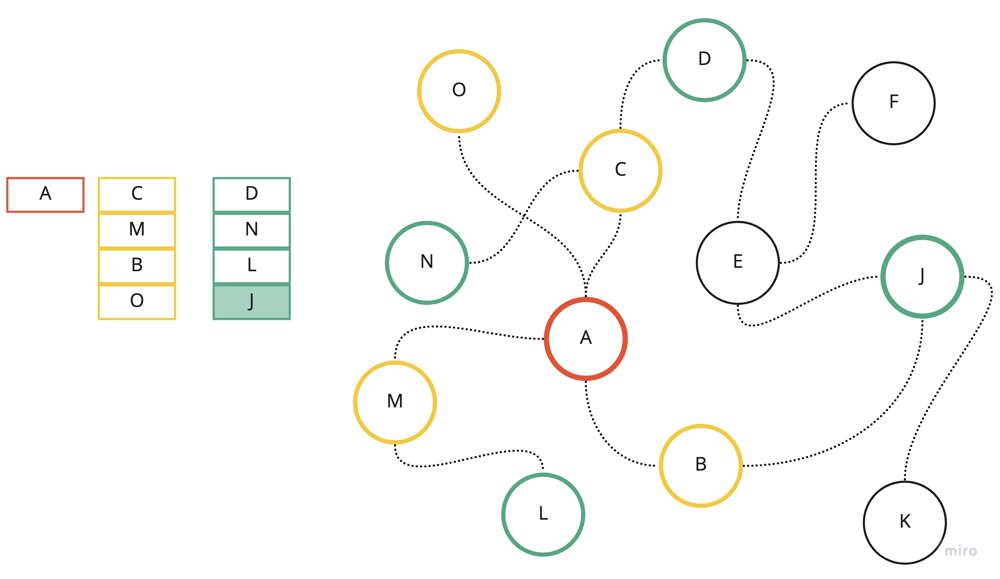
Union-Find Visualization

Topological Sort: Ordering Tasks

• Definition: An ordering of vertices in a directed graph where for every directed edge uv, vertex u comes before v.

Example Implementation (Kahn's Algorithm) in Java:

import java.util.*;

public class TopologicalSort {
    public static List<Integer> topologicalSort(int numVertices, Map<Integer, List<Integer>> graph) {
        int[] indegree = new int[numVertices];
        for (int node : graph.keySet()) {
            for (int neighbor : graph.get(node)) {
                indegree[neighbor]++;
            }
        }

        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < numVertices; i++) {
            if (indegree[i] == 0) {
                queue.add(i);
            }
        }

        List<Integer> sortedOrder = new ArrayList<>();
        while (!queue.isEmpty()) {
            int current = queue.poll();
            sortedOrder.add(current);

            for (int neighbor : graph.getOrDefault(current, new ArrayList<>())) {
                indegree[neighbor]--;
                if (indegree[neighbor] == 0) {
                    queue.add(neighbor);
                }
            }
        }

        if (sortedOrder.size() != numVertices) {
            throw new IllegalArgumentException("The graph contains a cycle!");
        }
        return sortedOrder;
    }

    public static void main(String[] args) {
        Map<Integer, List<Integer>> graph = new HashMap<>();
        graph.put(0, Arrays.asList(1, 2));
        graph.put(1, Arrays.asList(3));
        graph.put(2, Arrays.asList(3));
        graph.put(3, new ArrayList<>());

        int numVertices = 4;
        System.out.println("Topological Sort: " + topologicalSort(numVertices, graph));
    }
}

Notes on Topological Sort

• Indegree Calculation: Nodes with no incoming edges are processed first.

• Queue-Based Processing: Ensures nodes are processed in the correct order.

• Applications:

  • Task scheduling.

  • Resolving package dependencies.

  • Finding course prerequisites.

Topological-Sort Visualization

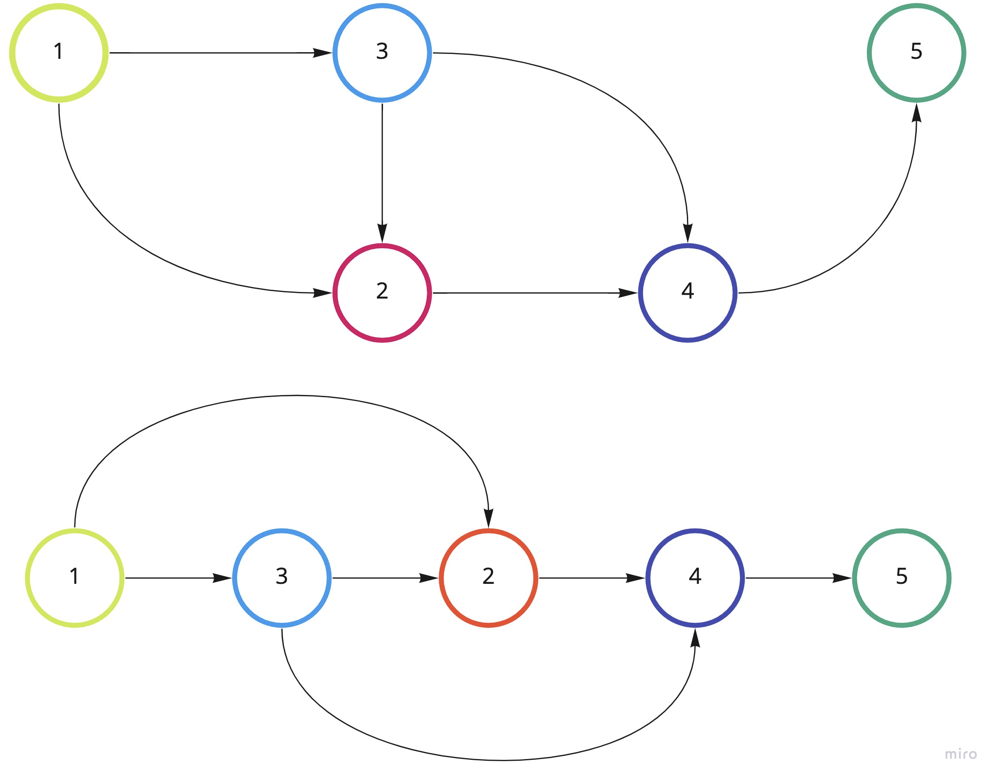
Practice Problems

• DFS Problems:

  ◦ Number of Islands:
  Count the number of distinct islands in a 2D grid, using DFS to explore connected land.

  ◦ Flood Fill:
  Implement the flood fill algorithm to change the color of a connected region in an image.

  ◦ Longest Increasing Path in a Matrix:
  Find the longest increasing path in a matrix where each step must be to an adjacent cell.

  ◦ Evaluate Division:
  Evaluate division of variables using DFS in a graph of equations and values.

  ◦ Robot Room Cleaner:
  Design a robot to clean a room represented by a grid, using DFS to explore the area.

  ◦ Most Stones Removed with Same Row or Column:
  Find the maximum number of stones that can be removed by choosing stones from the same row or column.

  ◦ Reconstruct Itinerary:
  Reconstruct an itinerary from a list of flights using DFS for path reconstruction.

  ◦ Tree Diameter:
  Find the diameter (longest path between any two nodes) of a tree using DFS.

  ◦ Accounts Merge:
  Merge accounts based on common email addresses using DFS to group connected accounts.

• BFS Problems:

  ◦ Flood Fill:
  Perform flood fill on a 2D grid to change the color of a connected region.

  ◦ Number of Islands:
  Count the number of distinct islands in a grid using BFS to explore land.

  ◦ Word Ladder I:
  Find the shortest transformation sequence from one word to another using BFS.

  ◦ Word Ladder II:
  Find all the shortest transformation sequences between two words using BFS.

  ◦ Evaluate Division:
  Evaluate division of variables using BFS to traverse through equations.

  ◦ Get Watched Videos by Your Friends:
  Find all videos watched by friends using BFS to explore friend connections.

  ◦ Cut Off Trees for Golf Event:
  Find the minimum number of steps to cut trees in a grid using BFS.

• Dijkstra's Problems:

  ◦ Path With Maximum Minimum Value:
  Find the path with the maximum minimum value in a grid using Dijkstra’s algorithm.

  ◦ Network Delay Time:
  Find the time it takes for all nodes to receive a signal from a source node.

  ◦ Path with Maximum Probability:
  Find the path with the maximum probability between nodes in a graph.

  ◦ Path With Minimum Effort:
  Find the path with the minimum effort to reach the destination.

  ◦ Cheapest Flights Within K Stops:
  Find the cheapest flight path within a maximum of K stops using Dijkstra’s algorithm.

• Union Find Problems:

  ◦ Number of Islands:
  Use Union Find to count the number of connected islands in a grid.

  ◦ Largest Component Size by Common Factor:
  Find the largest connected component in a graph using Union Find.

  ◦ Most Stones Removed with Same Row or Column:
  Find the maximum number of stones that can be removed using Union Find.

  ◦ Number of Connected Components in an Undirected Graph:
  Use Union Find to find the number of connected components in a graph.

• Topological Sort Problems:

  ◦ Course Schedule:
  Determine if it's possible to finish all courses based on prerequisite dependencies.

  ◦ Course Schedule II:
  Find the order in which courses should be taken to finish all courses.

  ◦ Sequence Reconstruction:
  Check if a sequence can be reconstructed uniquely from its subsequences.

  ◦ Alien Dictionary:
  Determine the correct order of characters in an alien language using topological sort.

Final Thoughts

• Graph theory's vastness and complexity initially seemed like climbing a top that had no end, but breaking it down into manageable pieces made it approachable.

• The journey from basic graph concepts to implementing complex algorithms was challenging but rewarding. Regular practice and persistence were key to understanding these fundamental concepts in computer science.

• Instead of trying to learn everything at once, I broke it down into small pieces. Each day, I'd tackle one small part. Some days I'd work on basic searches, other days I'd try to solve simple problems. Slowly but surely, things started making sense.

• This is Part 1 of my learning, and I'm currently working on Part 2, exploring and learning new graph algorithms.