Individual Scores in Choice Models, Part 4: Inspecting Model Fit with RLH

Chris ChapmanChris Chapman
31 min read

I expect this to be the last post of my “Individual Scores in Choice Models” series. To recap the series so far:

In this 4th post, I examine the Root Likelihood (RLH) fit measure, which summarizes how well MaxDiff (or Conjoint) utilities fit the observed data from survey respondents. It’s a long post, partly because the concept needs explanation, but also because I want to share closely-related ideas along the way.

This is only a partial discussion of quality assessment overall, because there are many ways to review data quality and model fit. You should add RLH inspection to other methods you might already use, such as identifying speeders. (However, I have warnings below about filtering respondents!)

As always, I share R code along the way. You can follow along live with the actual data — thanks to the generous sharing of anonymized data by the Quant UX Association!

Get the Data to Follow Along

The data here are individual estimates of interest in Quant UX training classes for N=308 mostly UXR respondents, as assessed on a MaxDiff survey. You can find the details in Post 1.

The following code loads the data needed for this post, and renames the variables to be shorter & friendly:

# get the data; repeating here for blog post 4, see post 1 for details
library(openxlsx)   # install if needed, as with all package calls
md.dat <- read.xlsx("https://quantuxbook.com/misc/QUX%20Survey%202024%20-%20Future%20Classes%20-%20MaxDiff%20Individual%20raw%20scores.xlsx")   # 
md.dat$Anchor <- NULL
names(md.dat)[3:16] <- c("Choice Models",  "Surveys",       "Log Sequences",    "Psychometrics", 
                         "R Programming",  "Pricing",       "UX Metrics",       "Bayes Stats",
                         "Text Analytics", "Causal Models", "Interviewer-ing",  "Advanced Choice", 
                         "Segmentation",   "Metrics Sprints")
classCols <- 3:ncol(md.dat)    # generally, Sawtooth exported utilities start in column 3

Model Fit Background: What is RLH?

[This section is long because I explain RLH conceptually, using simple examples. If you already understand RLH (or don’t care!), skip to the next section.]

RLH stands for “Root Likelihood” and it expresses the degree to which a fitted model matches observed data from respondents. RLH is usually calculated for observations in the training data (those for whom a model was fit). That’s because those are the observations for which we have individual level estimates.

Side note: in principle we could calculate RLH for any set of observations given a set of utility scores. For instance, we might calculate how well new observations match the utilities for a particular segment or an overall sample. That is rarely done in my experience, so I’ll just note it and not explore further.

Let’s break down the term “root likelihood” to see what is going on. First: "likelihood”. For a single observation, the likelihood is the odds that the single observation would have occurred, according to our model. For example, suppose we have a MaxDiff set of items A, B, C, and D. Further imagine that we have the following utility scores: Item A is preferred for a particular individual, with a utility of +1.0, while items B, C, and D have utilities +0.5, -0.8, and -1.2 respectively.

Given those utilities, and under the MNL (multinomial logit) share-of-preference formula, the preference share for item A for this respondent, as calculated in R syntax, is exp(1.0) / sum(exp(c(1.0, 0.5, -0.8, -1.2))) or 0.53. That means that on a task showing A, B, C, and D, the respondent is estimated to have a 53% chance of choosing their most preferred item, Item A. There leaves an estimated 47% chance they would choose one of the other options (most likely Item B, but potentially C or D).

If the respondent did in fact choose Item A, then the likelihood value of that observation is 0.53 (the relevant share of preference for that choice). In this case, the model is doing pretty well because it correctly predicted the most likely choice.

On the other hand, if they chose Item D, then the likelihood — according to the estimated utilities — would be exp(-1.2) / sum(exp(c(1.0, 0.5, -0.8, -1.2))) or a 5.9% chance and a likelihood value of of 0.059. In this case, unlike the odds for Item A above, the model is not doing well because its “agreement” with the actual choice was only 0.059.

In short, the “likelihood” part of the term calculates the odds we should have seen each individual response, according to the model. When the value is higher, it means that the data we saw was more “likely” according to the model.

Next: “root”. Given multiple observations, we can calculate their joint likelihood by multiplying the separate odds. For example, suppose that we ask the exact same two tasks in a row as we listed above, and that our respondent chooses A on one, but D on the other task. The likelihood of those two observations together is 0.53 * 0.059 or 0.031. But that number is across two trials. To get a single estimate, we take its square root, or sqrt(0.53 * 0.059) which is 0.177. That means that the root likelihood (RLH) of our two observations, given the estimated model, is RLH = 0.177.

Side note: you might notice that taking the simple product of multiple likelihood scores assumes that they are probabilities of independent events … but are the events here “independent”? Isn’t it the case that choosing A on one task is highly correlated with the odds of choosing A on another task?

The answer, conceptually speaking, is that dependence across tasks is already included in the model when it estimates the utility scores. Given the fact that we have estimates for A, B, C, D, and so forth, we can now ask, in effect, “what happens when we draw random samples of comparisons?” (the tasks that were given to the respondents). There is no dependence in how those tasks were drawn — they are independent of the model — so the probabilities can be considered independent for this purpose.

To be sure, one might pose higher-order questions about interactions, such as the degree to which the exact task order may influence responses, such that they interact with the model in a non-independent way. However, such questions rapidly become unanswerable — and most likely would have little effect on a model fit score. A general assumption of independence between tasks seems to work well.

If we have more than two observations, as we usually would in a MaxDiff survey, we just take an appropriate fractional exponent instead of the square root. If we have 10 trials, we would multiply 10 separate odds and then take the 10th root (exponentiate to 1/10) of the product.

In R, such a calculation looks like this:

(individualOdds <- seq(0.01, 0.99, length=12))  # placeholder for the likelihoods
(rlh <- prod(individualOdds) ^ (1/length(individualOdds)))

In the first line of this code, I create a set of fake odds between 0.01 and 0.99, so we will have values to work with. In real data the odds would be calculated from utilities and observations as noted above. The second line is the key point: it computes the root likelihood. First it multiplies all the odds (prod()) and then takes the Xth root of them (^(1/length(individualOdds))).

Side note about that calculation using prod() for repeated multiplication: this is the didactic & conceptual way to calculate RLH. See the code below for a better computational version.

In case you’re wondering … no, you don’t have to calculate RLH on your own from the data. A platform like Sawtooth Software Discover or Lighthouse Studio will calculate RLH and include it automatically in the individual level data. I’m showing the calculations only for one reason: so you will know how it works!

By the way, RLH works exactly the same way for conjoint analysis. After estimating a conjoint utility model, we can calculate the odds of each observed choice based on those utilities, and then take the Xth root to calculate RLH.

What You Can Do with RLH

In general, RLH can be used in two ways:

  • As a high level signal of quality, namely whether your data are markedly suspect

  • As a way to filter out potentially non-informative respondents

As for quality, I don’t say that RLH indicates whether a data set or a respondent is “good.” No single metric can assess that. However, if RLH is markedly low — as we explore below — then it indicates potentially serious problems. In particular, if the median RLH in a sample falls below a reasonable threshold (keep reading) then you have a problem such as inconsistent respondents, a poor survey, or a poor model.

Beyond the high level diagnostic value, some analysts use RLH to filter out so-called “bad” respondents. Typically this is done by setting a minimum threshold for an acceptable RLH (again, keep reading!), removing respondents who are below that value, and then estimating the model again without them.

In practice, I almost never remove respondents due to RLH for four reasons:

  1. RLH does not identify whether responses are “bad”. It only says how likely they are, conditional on the model that was estimated from them. I discuss this below at some length, near the end of this post.

  2. Instead of removing respondents, I try instead to use high quality data sources. I don’t believe analytics can “rescue” bad data sources.

  3. Choice models are robust to random answers, straight lining, speeding, and similar “bad” response patterns. So, if even a modestly large number of respondents are answering in those ways, it is unlikely to seriously affect the ultimate estimates (at least at the level of sample averages).

  4. Any method to remove “bad” respondents introduces other sources of bias. As one minor example: why not remove excessively high RLH respondents who are “too good”? Again, I say more below.

A counterargument to my position is the following: if a respondent’s RLH is near the value of “random” observations, then we are not learning much from them, so we might as well remove them from the model to be more precise and efficient. For reasons I discuss below, that is not the complete story and there is more to consider. We’ll get to that!

Meanwhile, before acting on RLH, we need to inspect it. We’ll do that next.

Examining RLH in the UXR MaxDiff Data

Now that you know how RLH works and what you can do with it, let’s look at the values from the Quant UX Association MaxDiff for N=308 respondents. Sawtooth’s data file helpfully includes the individual RLH values when it exports individual level data, so you don’t have to calculate anything.

Using the data set loaded above, we can set a friendly column name and start exploring:

names(md.dat)[2] <- "RLH"
summary(md.dat$RLH)

In our data, the MaxDiff RLH values range from 0.32 to 0.80, with a median of 0.60:

As always, it’s important to plot the values. The ggridges package makes nice density plots with the geom_density_ridges() function, including an option to fill in the individual points (jittered so they don’t overlap under the curve):

# density plot of the RLH values
library(ggplot2)
library(ggridges)
set.seed(98101)    # jittered points are slightly randomized
p <- ggplot(data=md.dat, aes(x=RLH, y=1)) +
  geom_density_ridges(jittered_points=TRUE, 
                      alpha=0.5, colour="darkblue") +
  xlab("Model fit score (RLH; > 0.3 is good)") +
  ylab("Relative prevalence (density)") +
  theme_minimal()

p

In the code above, I set y=1 because ggridges generally assumes that you have multiple series to plot overlapping density curves, identified with a nominal y variable. In this case, we have only one series, so I set a single dummy y value.

Here’s the result:

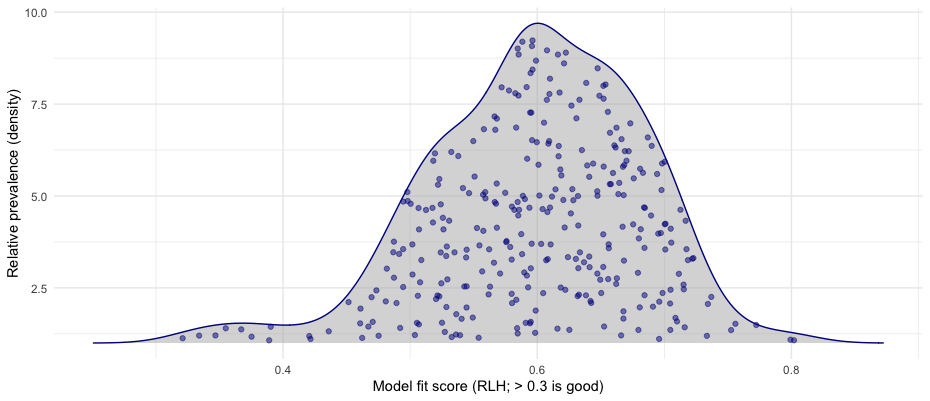
How do we interpret this chart? Well, I’ve already labelled the X axis with “\> 0.3 is good” … but the reason for that label will have to wait until the next section.

Accepting that cutoff value for a moment, we see a few things in the chart:

  • All of the individual fit values are “good” according to the purported cutoff value of 0.3.

  • The curve is nicely Gaussian (normal) in shape, which is a good thing … for reasons I won’t go deeply into. (Hint: it relates to assumptions of the HB model as well as random tasks, and assumptions of random variation across people.)

  • There is a small elevated tail on the lower end with RLH < 0.4. Those come from 2% of respondents for whom the model didn’t fit as well. We don’t know exactly why not, but perhaps they sped through it, or were distracted, or didn’t find the items or topic as relevant as other respondents did.

So we’ve seen the results and understood how they are calculated. But what is a “good” value for RLH? Is it OK that our median is 0.60? Why not 0.30 or 0.90?

In the next section, I discuss the threshold levels that make RLH “good” or not.

Are Those Values Good or Bad? What should we Expect?

In this section, I briefly discuss 2 heuristics that build intuition around RLH expectations. In following sections, I’ll look at a code-based analysis in R; and then mention another approach suggested by Sawtooth that uses random data.

For the first heuristic, a “good” value for RLH will be substantially better than random chance. For a MaxDiff (or Conjoint) task, one way to consider random chance would be if every item had the same likelihood of being chosen. For example, if a MaxDiff task has C=5 items on each screen, then we might say that each one has a random likelihood of 1/C = 1/5 = 0.20.

Put differently, our model should get 20% of the choices right merely by picking an item from 1-5 randomly. We want to do substantially better than that … let’s say we want to do “50% better.” That’s a heuristic cutoff but agrees with a lot of experience. Then we could set a minimum likelihood of RLH = 0.30 to be better than that form of random chance.

For the second heuristic, we note that the one above is a somewhat simplistic version of random chance. We might instead say, “we know that items will vary in preference, so there’s no way they will all have 1/C odds.” A different way to look at random chance incorporates that concept. This will help us look not at the minimum acceptable RLH (as above) but at what we might expect for a good RLH value.

Suppose we assume that 5 items will have relative preference of (1, 2, 3, 5, 8). I’m making that up (using the Fibonacci sequence) just as a heuristic example. However, it’s not an unreasonable set because real world results often find 1-3 items that are “winners” plus a long tail of less-preferred items.

In R, we could calculate the RLH expected given those odds. We will assume that the model knows those odds that they perfectly match the item chosen on the tasks (i.e., that the respondent chose the item that aligns with the most-likely item). Here’s the code in R:

# back of the envelope
# pick some preference distribution and calculate odds
itemOdds <- c(1, 2, 3, 5, 8)           # relative preference for 5 items
itemOdds <- itemOdds / sum(itemOdds)   # rescale so they sum to 1.0
max(itemOdds)          # relative odds for the most-preferred item

That is a value of itemOdds = 0.42. So — under this one set of preferences, a model that correctly predicted the choice of the most-preferred item — would have a likelihood or RLH of 0.42. That suggests heuristically that an RLH of approximately 2/C (2/5 = 0.40) may be pretty good.

BTW, you might note that this also means that a perfect model, given those preferences, would be wrong in its predictions ~60% of the time. We can’t expect our models to be extremely accurate about point predictions exactly because people’s preferences are tendencies — they are not 0/1 values. For example, someone who would register for one class may also have a high chance of registering for another one. Choice models are helpful because they tell us what is more or less likely, on average, and how options compare to one another … not because they exactly predict individual events.

Putting this value together with the previous minimum heuristic, where 1.5/C may be a lower cutoff, we could form a range bounded like this:

  • Rough cutoff: < approx 1.5/C. For example, with 5 items shown at a time: 1.5/5 = 0.30. For 4 items shown at a time: 1.5/4 = approx 0.375 as a lower minimum.

  • Clearly good: = approx 2/C. For example, with 5 items: 2/5 = approx 0.40.

In other words, RLH is heuristically “good” when it is in or above the range of (0.30 — 0.40) when we test 5 items at a time.

Are you thinking, “Wait! That’s a pretty low value. I would have expected a good model to have RLH of 0.80 or 0.90 or 0.99!”

You’re right — it is not a high value. We’ll see more about that below. Meanwhile, it is always important to remember that respondents usually find multiple items to be interesting, and might prefer one or another more or less randomly. For example, I like Dr. Pepper Zero soda … but a model of my preference is not 100% Dr. Pepper! I often drink other things, especially water, but also coffee, Gatorade, tea, Zevia soda, and so forth. That means we should not expect a model to do any better than to capture my most likely choice, at the level of its relative share — a likelihood much lower than 1.0.

Key point: these heuristic results should help you build intuition about why RLH will not be especially high in real data.

You might wonder next, “Can we quantify that better, not just using a thought exercise?” We’ll do that systematically in the next section.

Deep Dive: R Code to Simulate RLH Values

This section is a moderately deep dive into R simulation! If you are satisfied with the heuristics in the previous section, you can skip it … unless you like R as much as I do.

The previous section described why RLH in the range of RLH > roughly 1.5/C — which is to say, 0.30 for a MaxDiff with 5 items shown at a time — may be a reasonable minimum cutoff for a good respondent using heuristic logic. We also saw that RLH ~ 2/C — or 0.40 for 5 items — may indicate a particularly good fit between the observations and model. Now we’ll examine the expectation more systematically using code.

Here’s what I’m going to do. The short version is that I’ll do many, many random iterations of the kind of heuristic I showed above, for different sets of preference values. That will inform us as to the generally expected range of RLH values when the observations and data match perfectly.

More specifically, the code will simulate “respondent utilities and choice” as follows:

  • Draw utilities as random normal values with mean=0 and some standard deviation (I’ll come back to that). This mirrors the assumptions of the HB models used to estimate MaxDiff utilities, so the values will be realistic.

  • Draw random sets of “items” from those, 5 at a time, to mimic the utilities that might apply to a particular MaxDiff task.

  • For each set of 5 item utilities, calculate the share of preference for the single most-preferred item. That gives us the highest possible likelihood value for that task (if the respondent always chose the most-preferred item, according to the model)

  • Do the above using K [“nItems”] = 14 items (because that matches the number of items on the Quant UX survey that provided our data)

  • For each simulated “respondent”, do this for C [“nShown”] = 5 items at a time on each screen, for S [“nScreens”] = 6 total screens (because that matches the length of the Quant UX survey).

  • Simulate all of the above a total N [“nIter”]=10000 times (“respondents”)

Here is code that sets up the initial conditions for all of that. It also sets a random number seed to make the analysis repeatable:

nIter    <- 10000            # how many times to sample nItem MaxDiff simulations
nItems   <- 14               # number of items in a MaxDiff set
nShown   <- 5                # number of items shown on a single screen
nScreens <- 6                # number of screens in our survey
rlhDraws <- rep(NA, nIter)   # hold the results for each iteration
set.seed(98250)              # make it repeatable

Technical note: although MaxDiff utilities are always zero-centered (in their “raw” form estimated by an HB model), utilities vary from study to study and item to item in their standard deviation (SD). To draw random zero-centered, simulated utilities, we need to specify that variance. To get an SD value for this simulation, I look empirically at the Quant UX data and use the median SD (drawSD) for the items in that study:

summary(unlist(lapply(qux.md[ , classCols], sd)))   # answer: somewhere around sd ==(2.2, 2.6)
(drawSD  <- median(unlist(lapply(qux.md[ , classCols], sd))))

Now we’re all set up and ready to run the simulation. Following is the code. First I’ll give the whole chunk, and then I’ll discuss it below.

for (i in 1:nIter) {
  # set up 1 respondent "trial"
  pwsResp     <- rnorm(nItems, mean=0, sd=drawSD) # "nItems" random normal, zero-centered simulated part worths
  pwsResp     <- scale(pwsResp, scale=FALSE) # recenter to make sure they're zero-sum

  # iterate over nScreen tasks per respondent
  drawMax <- rep(NA, nScreens*2)             # hold the results across the screens for one respondent
  for (j in 1:nScreens) {
    pwsDrawn    <- sample(pwsResp, nShown)   # get the part worths for 1 simulated task  
    # "best" choice
    pwsExp      <- exp(pwsDrawn)             # exponentiate those part worths
    pwsMaxShare <- max(pwsExp) / sum(pwsExp) # our best (most likely) prediction would be the max utility item
    drawMax[j*2 - 1]  <- pwsMaxShare
    # repeat for the "worst" choice
    pwsExp        <- exp(-1 * pwsDrawn)      # exponentiate part worths for the "worst" choice direction
    pwsMaxShare   <- max(pwsExp) / sum(pwsExp)   
    drawMax[j*2]  <- pwsMaxShare
  }
  # calculate RLH from those observations
  rlh         <- exp(sum(log(drawMax[drawMax > 0]), na.rm=TRUE) / length(drawMax))    # safer equivalent of "prod(drawMax) ^ (1 / length(drawMax))"
  rlhDraws[i] <- rlh
  # add a bit of error checking, just in case of an off by one error etc :-/
  if (length(drawMax) != nScreens * 2) warning("The vector of partworths is off somewhere!", i, ":", drawmax)
}

This code has five main parts:

  1. An outer loop iterates over the 10000 (nIters) simulated “respondents” (Line 1). For each of those iterations:

    1. It draws zero-centered utilities for the 14 items (Lines 3-4) for that 1 simulated respondent

    2. An inner loop iterates over 6 MaxDiff choice “trials” (Line 8), and inside that:

      1. It makes a trial with 5 randomly chosen items to be compared on 1 choice task (Line 9)

      2. It chooses the most likely Best & Worst on that random trial and calculates the likelihoods for those choices (Lines 11-17).

      3. When it’s done with the 6 tasks, it calculates RLH for the set of 12 observed Best & Worst “choices” for that respondent (6 Best + 6 Worst), and saves that result (Lines 20-21)

The error check line at the end was just some defensive coding that occurred to me along the way (nothing in particular prompted it; I just like to code defensively). It never triggered.

Side note: this code assumes that the overall, upper level means of all items are also zero. One could instead structure those; that’s a longer discussion. A more general approach would be to iterate over different sets of part worth scores; different survey lengths; and different sizes of choice sets. The code above could serve as the basis for a function that is refactored for use inside a larger and more general set of loops and/or parameter variations. That would be a good exercise!

BTW, you will see that RLH here is computed with a different formula than above (but one that is mathematically equivalent). Why? Because, when many odds are multiplied together, they will quickly underflow real number calculation engines. By taking the log() of them and then adding the logs rather than multiplying, we avoid that problem.

Side note: R can handle multiplying 12 probabilities — but if the survey were longer, then we could have problems. It’s always good to anticipate such things and proactively avoid them when coding!

Results from the Simulation

After running this code, we have RLH scores for 10000 simulated “respondents”. As a reminder, the code has assumed that all of the “observed” choices aligned perfectly with the most likely, most preferred items, according to the simulated individual level utilities. Thus it sets an upper bound for expectations of RLH. (Caveat: this assumes there is no “none of the above” option. I discuss that below.)

Here’s code to plot the results, slightly adapting the density chart code from above:

# density plot
set.seed(98195)    # jittered points are slightly randomized
p <- ggplot(data=as.data.frame(rlhDraws), aes(x=rlhDraws, y=1)) +
  geom_density_ridges(jittered_points=TRUE, 
                      alpha=0.1, colour="darkblue") +
  xlab("Model fit score (RLH; > 0.3 is good)") +
  ylab("Relative prevalence (density)") +
  ggtitle("RLH Simulation, Perfectly Made Choices (N=10000)") +
  theme_minimal()

p

And the resulting chart:

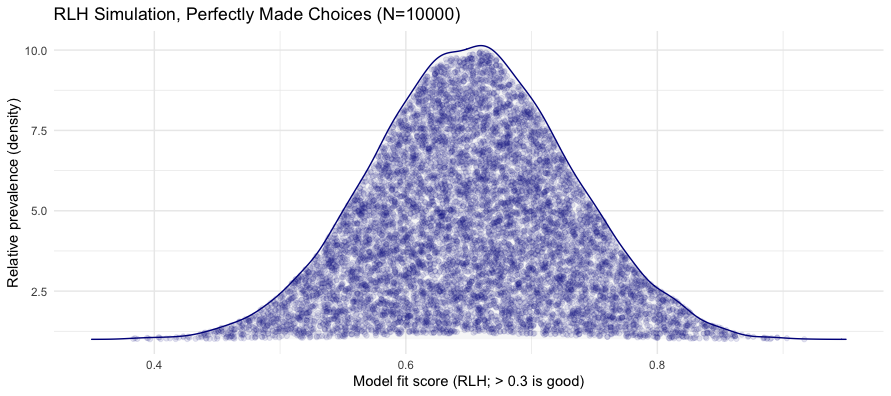
This tells us that when respondents make choices perfectly in alignment with their estimated preferences — with other assumptions about utility scores and survey parameters, as above — we can expect those upper-bound RLH values to fall between roughly 0.4 and 0.9, with most falling between 0.5 and 0.8.

In other words, if we have no other information except that a respondent shows RLH=0.5 or RLH=0.4, it could in fact be a maximum, perfect RLH score for them. In general, we should not expect — and instead, should be surprised, because it is near “perfect” — to see RLH >= 0.6 or so.

As we saw above, our actual UXR data had median RLH = 0.60. That suggests that our respondents are not too far below “perfect” in their response patterns.

Put differently, UXRs are great respondents when a survey is relevant and motivating for them! (In a consumer sample, I would expect substantially lower RLH, more like a median of 0.40.)

We can compare the two sets of results — actual vs. UXR — using the same kind of density plot. Here’s the code:

# combined density plot (using random subset of simulated data)
compare.df <- data.frame(RLH    = c(md.dat$RLH, rlhDraws),
                         Source = rep(c("UXR", "Sim"), 
                                      times=c(length(md.dat$RLH), 
                                              length(rlhDraws))))

# density plot
set.seed(98102)    # jittered points are slightly randomized
p <- ggplot(data=compare.df, aes(x=RLH, y=Source, color=Source)) +
  geom_density_ridges(jittered_points=TRUE, 
                      alpha=0.1) +
  xlab("RLH") +
  ylab("Relative prevalence (density)") +
  ggtitle("RLH Comparison: UXR Data vs. 'Perfect' Simulation") +
  theme_minimal()

p

In this code, I first combine the two data sources into a single data set. Then I use the same density plot functions, adding the “Source” of each data point (UXR data vs. simulation) as the y variable, which will stack the results as two density curves.

Here’s the chart:

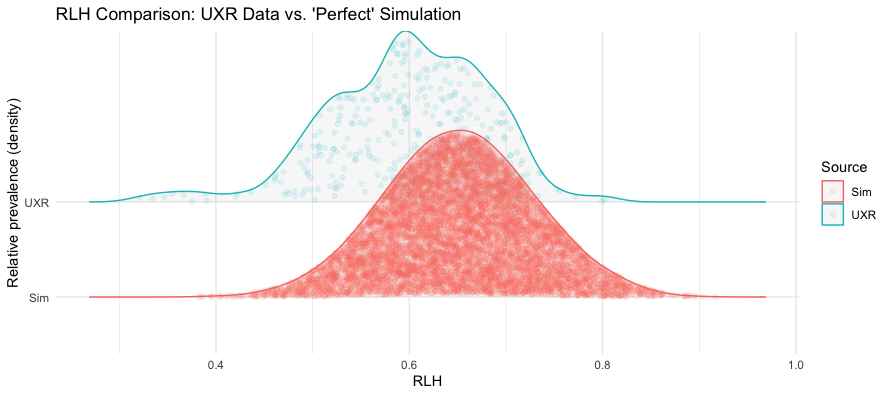
As you can see, the UXR data is pretty close to “perfect.” Again, I would not expect this in most data sets! Usually I would be happy with median RLH > 0.4 or so. But this comparison highlights once more what we might expect as the upper bound of reasonable RLH.

Looking a bit further, we see an interesting suggestion of tri-modality in the UXR distribution of RLH. On the right hand side (peaking ~0.65), there is a suggestion of a group that looks exactly like the “perfect” data. Then there is a middle peak suggesting a group (peaking ~0.60) that looks slightly less than perfect. Finally, there is a left hand peak (peaking ~ 0.52) that shows lower RLH for some reasons (there are many) — which is not at all “bad” by any means, but contrasts the two higher modal peaks.

Overall I wouldn’t make much of that observation; I’m just highlighting it as a signal of potential additional questions we might have about respondent style, sources, quality, etc., in a sample.

Another Approach: RLH Cutoffs via Random Data

Another approach to using RLH as a cutoff comes from the choice modeling experts at Sawtooth (Orme, 2019 PDF). They noted two things:

  1. RLH for “random” responses can vary on a given survey due to the details of the survey’s experimental design (e.g., some tasks are “harder” or “easier” relative to the model overall)

  2. Their platform allows creation of random “respondents” who take the actual survey.

Putting those together, they suggested using the random respondent method in their platform to empirically determine a point at which the RLH for a particular respondent is clearly below the expectation for a random respondent. Specifically, identify a percentile cutoff, such as the 95th percentile (highest 5%) of RLH in the simulated random respondents. After identifying that point, filter out respondents below that; and then run the overall model again without them.

For step by step details, see the excellent white paper (Orme, 2019 PDF). Unlike the heuristic R code above, this method exactly fits your own survey. (BTW, that method could be used in any platform that offers random responses plus individual RLH calculation.)

However, I will also note that one should be cautious about filtering — as Orme notes in the white paper and as I will discuss next.

Caveats: RLH Fit Values and Filtering Responses for “Data Quality”

Before we finish, I want to clarify two things: that RLH is not about respondents but is about the fit between observations and model; and that filtering respondents with any method is risky.

RLH is not about respondent quality

Throughout the post, I’ve described how RLH relates to the mutual likelihood of a model and observations. I want to be very clear that this does not necessarily say anything about respondent quality.

Why not? Consider an edge case (actually somewhat common) when a respondent accurately reports that they do not like any of the items on a MaxDiff. Perhaps they are completely uninterested in the features or project … and they truthfully and diligently report that disinterest. Suppose that the model accurately says that their utilities are ~0 (±error) for every item.

In that case, the RLH for this diligent respondent on a C=5 items-at-a-time survey would approximate exp(0) / (5*exp(0)) = 1/C … indistinguishable from the expectation for a completely random respondent!

That means that low RLH is only a signal that something is wrong. It may be that the respondents are answering randomly. Yet it may be that your items are unappealing, or that you are targeting the wrong audience, and respondents are accurately communicating that. In this case, filtering out low RLH respondents could be the exact wrong thing to do, because their disinterest may be important to know.

That doesn’t mean that RLH is useless. Rather, RLH is one diagnostic signal, and needs to be placed into context with other signals (such as observations from an in-person pilot study, which I always advocate).

BTW, RLH can also be exceptionally high for similar reasons — which may happen in particular when a conjoint survey or MaxDiff has a “none” option. If a respondent answers “no, I don’t want it” on every task, then their “none” utility will have a very large value.

Suppose a respondent’s “none” utility = 5.0, while 10 other items each have utility = -0.5. Then, on a C=5 task including “none”, their expected RLH = exp(5) / (4*exp(-0.5) + exp(5)) = 0.98.

That might indicate a “bad” respondent who simplifies the survey by picking “none” every time. OTOH, it might be a good respondent who accurately and importantly says that they don’t want the product. Again, the point is not that RLH identifies whether any respondent is good or bad. Rather, it must be used diagnostically with other knowledge and signals.

Filtering respondents is risky

I say this every chance I get, and won’t belabor it: anytime we filter respondents — whether that is from a screener, a model fit estimate, or whatever — we are introducing bias into the sample and its results.

The worst offenders that I see in this are are surveys that use multiple screening items to identify the “right” audience. For instance, they might want to find “intenders in the next 3 months in our target audience who are familiar with the product category and already use at least one product in the category.”

If a survey does that, stop and reconsider! Each of the 5 conditions in that hypothetical screener adds error. Unless the items have been psychometrically evaluated for prevalence, validity, and relation to the constructs of interest, then I would assume that filtering is adding a large and unknown degree of error, not reducing it!

The same considerations apply to filtering due to RLH as I described above. Filtering by RLH might reduce non-informative respondents … yet it also might remove respondents who are telling you something vitally important about their own disinterest. It’s important to know when RLH is low, because you can follow up by exploring why it is low.

Conclusion

I’ll finish with my recommended sequence of considerations for RLH with a choice modeling survey (MaxDiff or Conjoint Analysis):

  1. Always examine — through descriptive stats and plotting — the individual-level RLH estimates for your dataset in a choice model survey. Not just the overall average, but the individuals.

  2. If the curve is approximately normal, and only a small % are below a cutoff of 1.5/C (e.g., 1.5 / 5 items = 0.3 for a 5-item-at-a-time MaxDiff) … then I’d say RLH looks good, and don’t worry further about it. The UXR data above is an example of this. (Yay! UXRs are excellent respondents.)

  3. OTOH, if (say) >10% of respondents have RLH < 1.5/C, then you need to identify why that is occurring. The reasons might reflect any or all of these:

    1. Accurate responses of disinterest that are important to know

    2. A problem with the survey’s content, concept phrasing, programming, etc.

    3. The wrong target audience, perhaps indicating a need for new sample

    4. Low quality respondents due to response styles or panel characteristics

    5. Poor model fit for other reasons, such as inappropriate constraints on estimation

  4. There is no way to distinguish those five possibilities for low RLH without additional information, such as other signals, qualitative pre-testing of the survey, reconsideration of any unusual model choices, and so forth.

  5. Similarly, but less commonly, if your survey includes a “none” option, look out for an unusually high RLH peak (a moderate or high % of respondents with RLH > 0.8 or so).

In short, don’t use RLH as an automatic filter! Use it as a way to understand more about your data and to identify potential questions about respondents’ response styles.

I hope this discussion and the R code above will help you to use RLH with your data. Cheers!

All the R Code

As always, following is the R code for all of the blocks above, in one place. [BTW, the references to “12.x” are there because this code is continuous with code from the previous 3 posts of this series.]

##### 12. Data Quality / RLH

# 12.1
# get the data; repeating here for blog post 4, see post 1 for details
library(openxlsx)   # install if needed, as with all package calls
md.dat <- read.xlsx("https://quantuxbook.com/misc/QUX%20Survey%202024%20-%20Future%20Classes%20-%20MaxDiff%20Individual%20raw%20scores.xlsx")   # 
md.dat$Anchor <- NULL
names(md.dat)[3:16] <- c("Choice Models",  "Surveys",       "Log Sequences",    "Psychometrics", 
                         "R Programming",  "Pricing",       "UX Metrics",       "Bayes Stats",
                         "Text Analytics", "Causal Models", "Interviewer-ing",  "Advanced Choice", 
                         "Segmentation",   "Metrics Sprints")
classCols <- 3:ncol(md.dat)    # generally, Sawtooth exported utilities start in column 3

# simple calculations as described in the post
exp(1.0) / sum(exp(c(1.0, 0.5, -0.8, -1.2)))  # item A
exp(-1.2) / sum(exp(c(1.0, 0.5, -0.8, -1.2))) # item D       
0.53 * 0.059
sqrt(0.53 * 0.059)

(individualOdds <- seq(0.01, 0.99, length=12))  # placeholder for the likelihoods
(rlh <- prod(individualOdds) ^ (1/length(individualOdds)))

# 12.2 RLH
names(md.dat)[2] <- "RLH"
summary(md.dat$RLH)

# let's look at our UXR data
# density plot of the RLH values
library(ggplot2)
library(ggridges)
set.seed(98101)    # jittered points are slightly randomized
p <- ggplot(data=md.dat, aes(x=RLH, y=1)) +
  geom_density_ridges(jittered_points=TRUE, 
                      alpha=0.5, colour="darkblue") +
  xlab("Model fit score (RLH; > 0.3 is good)") +
  ylab("Relative prevalence (density)") +
  theme_minimal()

p

# 12.3
# how well might we *expect* to predict, if respondents answers agree *perfectly* with an estimated model?

# back of the envelope
# pick some preference distribution and calculate odds
itemOdds <- c(1, 2, 3, 5, 8)           # relative preference for 5 items
itemOdds <- itemOdds / sum(itemOdds)   # rescale so they sum to 1.0
max(itemOdds)          # relative odds for the most-preferred item

# code version
# we can do much better with a simulation model!
nIter    <- 10000            # how many times to sample nItem MaxDiff simulations
nItems   <- 14               # number of items in a MaxDiff set
nShown   <- 5                # number of items shown on a single screen
nScreens <- 6                # number of screens in our survey
rlhDraws <- rep(NA, nIter)   # hold the results for each iteration
set.seed(98250)              # make it repeatable

# we have to set distribution parameters for our simulated part worths
# in HB model, they are random normal, mean=0, ... but what sd should we use?
# look at empirical data to pick a reasonable sd
summary(unlist(lapply(qux.md[ , classCols], sd)))   # answer: somewhere around sd ==(2.2, 2.6)
(drawSD  <- median(unlist(lapply(qux.md[ , classCols], sd))))

for (i in 1:nIter) {
  # set up 1 respondent "trial"
  pwsResp     <- rnorm(nItems, mean=0, sd=drawSD) # "nItems" random normal, zero-centered simulated part worths
  pwsResp     <- scale(pwsResp, scale=FALSE) # recenter to make sure they're zero-sum

  # iterate over nScreen tasks per respondent
  drawMax <- rep(NA, nScreens*2)             # hold the results across the screens for one respondent
  for (j in 1:nScreens) {
    pwsDrawn    <- sample(pwsResp, nShown)   # get the part worths for 1 simulated task  
    # "best" choice
    pwsExp      <- exp(pwsDrawn)             # exponentiate those part worths
    pwsMaxShare <- max(pwsExp) / sum(pwsExp) # our best (most likely) prediction would be the max utility item
    drawMax[j*2 - 1]  <- pwsMaxShare
    # repeat for the "worst" choice
    pwsExp        <- exp(-1 * pwsDrawn)      # exponentiate part worths for the "worst" choice direction
    pwsMaxShare   <- max(pwsExp) / sum(pwsExp)   
    drawMax[j*2]  <- pwsMaxShare
  }
  # calculate RLH from those observations
  rlh         <- exp(sum(log(drawMax[drawMax > 0]), na.rm=TRUE) / length(drawMax))    # safer equivalent of "prod(drawMax) ^ (1 / length(drawMax))"
  rlhDraws[i] <- rlh
  # add a bit of error checking, just in case of an off by one error etc :-/
  if (length(drawMax) != nScreens * 2) warning("The vector of partworths is off somewhere!", i, ":", drawmax)
}

# density plot
set.seed(98195)    # jittered points are slightly randomized
p <- ggplot(data=as.data.frame(rlhDraws), aes(x=rlhDraws, y=1)) +
  geom_density_ridges(jittered_points=TRUE, 
                      alpha=0.1, colour="darkblue") +
  xlab("Model fit score (RLH; > 0.3 is good)") +
  ylab("Relative prevalence (density)") +
  ggtitle("RLH Simulation, Perfectly Made Choices (N=10000)") +
  theme_minimal()

p

# where does our observed data fall in the distribution?
ecdf(rlhDraws)(median(md.dat$RLH))               

# combined density plot (using random subset of simulated data)
compare.df <- data.frame(RLH    = c(md.dat$RLH, rlhDraws),
                         Source = rep(c("UXR", "Sim"), 
                                      times=c(length(md.dat$RLH), 
                                              length(rlhDraws))))

# density plot
set.seed(98102)    # jittered points are slightly randomized
p <- ggplot(data=compare.df, aes(x=RLH, y=Source, color=Source)) +
  geom_density_ridges(jittered_points=TRUE, 
                      alpha=0.1) +
  xlab("RLH") +
  ylab("Relative prevalence (density)") +
  ggtitle("RLH Comparison: UXR Data vs. 'Perfect' Simulation") +
  theme_minimal()

p

Citations

I’m reminding myself (and others) to systematically cite the important work others have done and that make R and other tools so valuable. Following are key citations for today’s code!

BTW, you can find citations for almost everything in R with the citation() command, such as citation("ggridges").

0
Subscribe to my newsletter

Read articles from Chris Chapman directly inside your inbox. Subscribe to the newsletter, and don't miss out.

quantuxconjointmaxdiffR Languagesurvey research

Written by

Chris Chapman
Chris Chapman

President + Executive Director, Quant UX Association. Previously: Principal UX Researcher @ Google; Amazon Lab 126; Microsoft. Author of "Quantitative User Experience Research" and "[R | Python] for Marketing Research and Analytics".