Algorithm: Recursion
 Adriene
AdrieneWhat’s recursion?
A function calls itself and runs again. An easy example below:
func rc() {
rc()
}
Every recursive function needs to have a base case or a stopping point. If the stop case doesn’t exist, the recursive function will keep running and endless call itself. So, a recursive must have two paths:
a recursive case
a base case to stop the recursive action
The example function above with adding a recursive case and a base case:
var counter = 0
func rc() string {
// base case: when counter exceeds 3, stop recursion and return "done!"
if counter > 3 {
return "done!"
}
// recursive case:
counter++ // 1. change state, the counter value
return rc() // 2. recursive call
}
return to return the outcome value! This return helps bubble up the value "done" straight to the very end. If the return is missing, the Go programming won't be executed. The terminal will show the message: missing return.// with return rc()
rc(rc(rc(rc())))
rc(rc(rc("done!")))
rc(rc("done!"))
rc("done!")
"done!"
// without return rc()
rc(rc(rc(rc())))
The programming won't execute. The terminal will show the message: missing return
Three rules when using recursion:
Identify the base case
Identify the recursive case
Add
returnwhen needed. Usually there are two place to usereturn. One is with the base case and another is with the recursive case.
The benefits of recursion are:
There are some downsides of recursion. One of the biggest problems of recursion is stack overflow. A function that keeps calling itself, like running an infinite loop, will add functions to the call stack. The computer allocates a part of the memory to the call stack to hold those called functions. But the memory is limited, and as it reaches to the limit, stack overflow happens. This situation will crush the program.
When to use recursion?
don’t know how many times the loop has to run
as using a tree data structure or converting something into a tree data structure
divide a task/ problem into some small tasks/ problems which are the smaller instances of the same task/ problem
each implement to solve the tasks/ problems is almost the same (doing the repeated subtask)
by combining the solutions of those subtasks/subproblems to obtain the result of the main task/problem
some searching and sorting algorithms (merge sort, quick sort, tree traversal, and graph traversal)
use cases example: doing traversal in a tree structure, HTML DOM traversal on a website, a nested object in Javascript
The tradeoff between the recursive way and the iterative way
Anything that can be implemented in a recursive way is able to be implemented in an iterative way. However, in some situations, the recursive ways are easier to write and accomplish DRY (Don’t repeat yourself.). But there are also downsides. Everytime the recursive function is called, it adds a frame to the call stack and might casue stack overflow. Also, memory space is expansive.
| Recursive | Iterative | |
| pros | good readability, DRY | not take much memory space |
| cons | take more memory, cause stack overflow | sacrifice readability |
Factorial
recursive version:
func findFactorialRecursive(num int) int {
// base case
if num == 1 {
return 1
}
if num == 2 {
return 2
}
// recursive case
return num * findFactorialRecursive(num-1)
}
func main() {
ans := findFactorialRecursive(5) // 120
fmt.Println(ans)
}
break down the steps: in () is the return value from the previous function
f(f(f(f(f()))))
f(f(f(f(1))))
f(f(f(2*1)))
f(f(3*2))
f(4*6)
5*24
iterative version:
func findFactorialIterative(num int) int {
var answer = 1
if num == 1 {
return 1
}
if num == 2 {
return 2
}
// <= means including the parameter value
for i := 2; i <= num; i++ {
answer = answer * i
}
return answer
}
func main() {
ans := findFactorialIterative(5) // 120
fmt.Println(ans)
}
break down the steps: ; separates what’s going on before and after each iteration
answer = 1, i = 2; 1 * 2, answer = 2
answer = 2, i = 3; 2 * 3, answer = 6
answer = 6, i = 4; 6 * 4, answer = 24
answer = 24, i = 5; 25 * 5, answer = 120
Fibonacci
The rule for the Fibonacci sequence is that each number is the sum of the two numbers before it. The sequence starts with 0 and 1. It will be 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …
recursive version:
func fibonacciRecursive(index int) int {
if index < 2 {
return index
}
return fibonacciRecursive(index-1) + fibonacciRecursive(index-2)
}
func main() {
fr := fibonacciRecursive(12) // 144
fmt.Println(fr)
}
Time complexity: O(2^n)
When the index is greater than 40, the programming runs slower and slower. Because the return value from each called function is the sum of the other two function
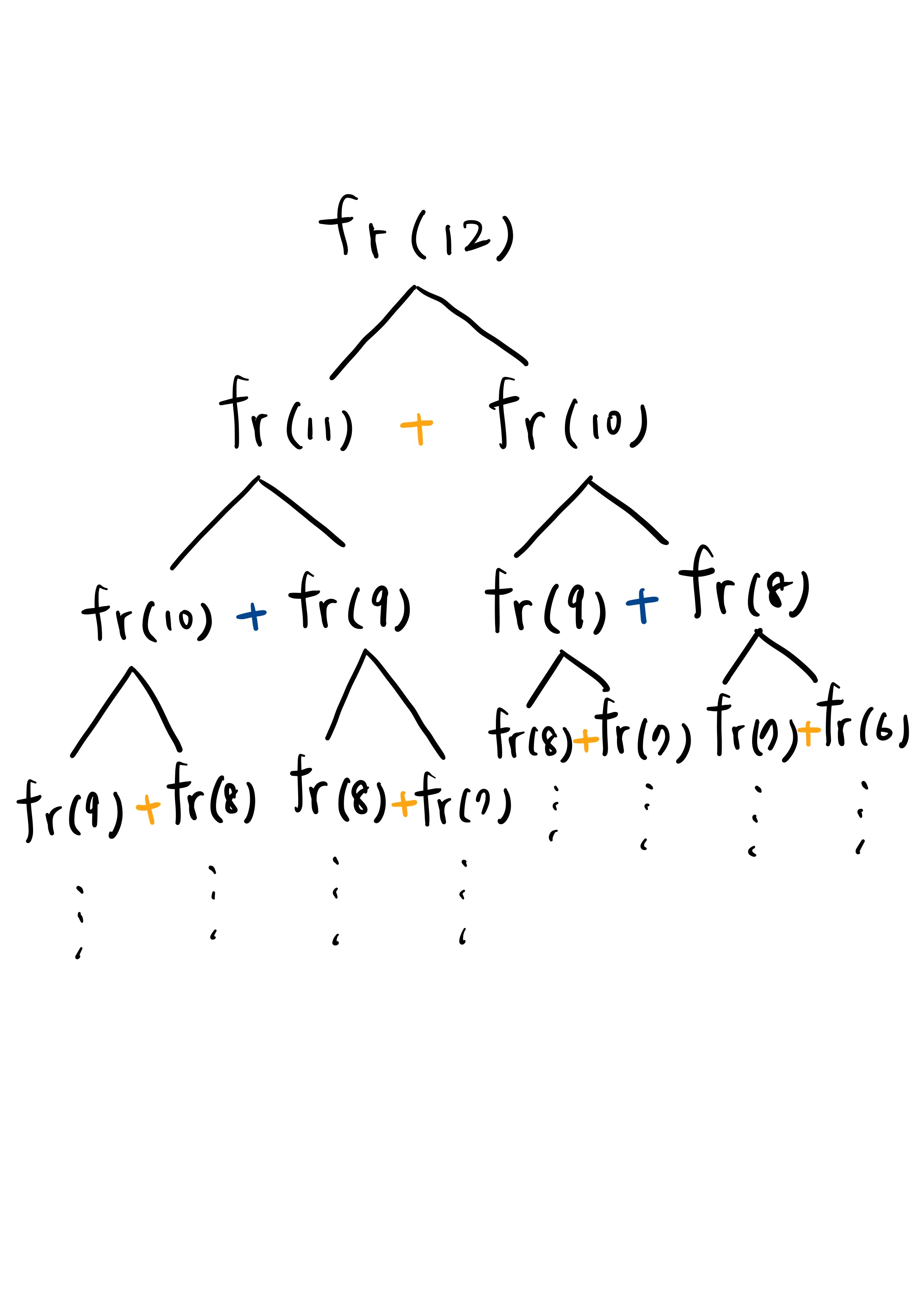
iterative version:
func fibonacciIterative(index int) int {
if index < 2 {
return index
}
f := []int{0, 1}
for i := 2; i < index+1; i++ {
num := f[i-1] + f[i-2]
f = append(f, num)
}
return f[index]
}
func main() {
fi := fibonacciIterative(12) // 144
fmt.Println(fi)
}
Time complexity: O(n)
As the index grows (index > 40), the iterative method is faster than the recursive one.
Maybe… this is the easier way to understand the concept of recursion
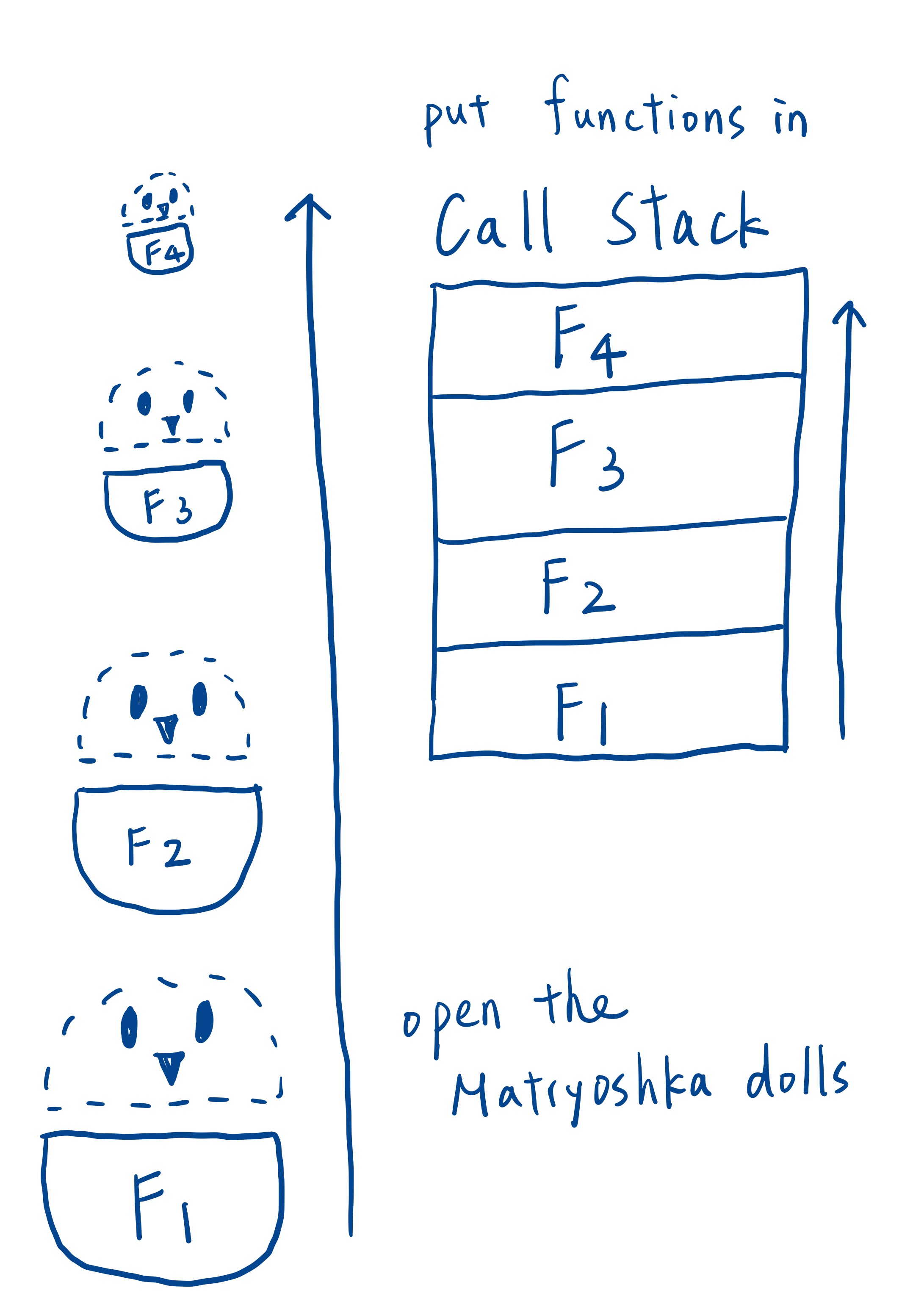
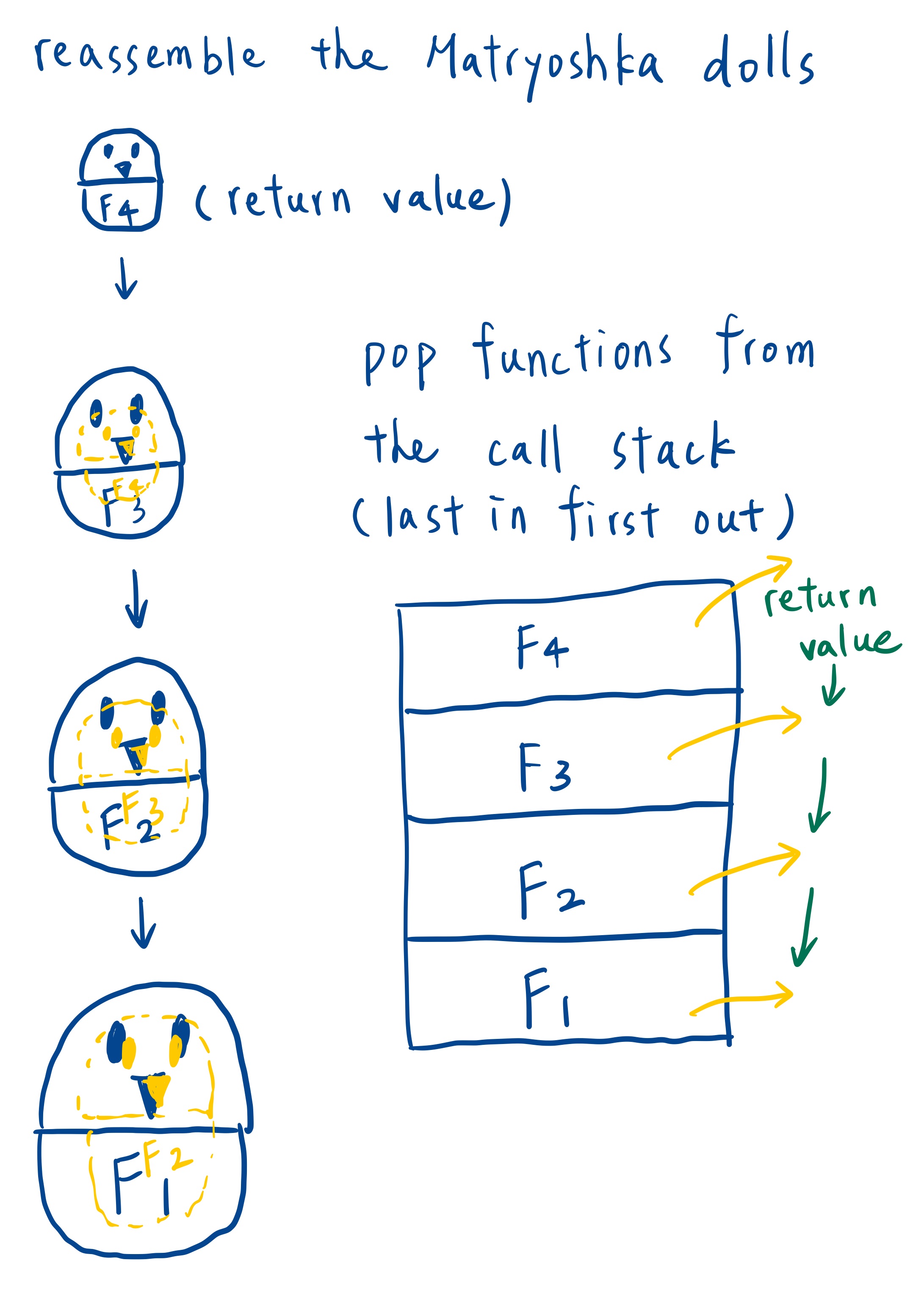
My way to understand how recursion works is to visualize recursion functions as a set of Matryoshka dolls. Opening each doll and set it aside is similar to call the recursive function and put it into the call stack one after another. Starting with the smallest doll, we gradually reassemble a doll by covering each one with its upper half part. Then, place it into the next larger doll. Each doll represents the return value from the function. As we place a smaller doll into the next larger one and close it, we are essentaily passing the return value back to the calling function. Again and again, repeat the process until the largest doll is completely reassembled, just as functions are popped from the call stack and return the value until the call stack is empty.
Subscribe to my newsletter
Read articles from Adriene directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
