"The Proof is Left for the Student..."

In my previous casual chronicle regarding Sangaku there was an equation which I did not give a proof for:

An equation for a chord of height \(h\) (from center) thru a circle with radius \(R\)

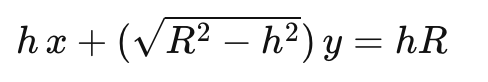
As one of my professors, the great Ralph Stanton often said, “this will be left to the student”. So, as one of his students years ago, I will give that proof here, but first a little background on graduation, grad school, and Professor Stanton.

CP/M, Graduation, Micro-Soft

One of the main reasons I went to Waterloo for graduate school was that I had no job offer after graduating from University of Manitoba in 1982. The oil patch had dried up, Canada had already been in a recession and it was getting worse, and there literally was no hiring.

There was some activity from the US though, and one company on campus was offering a signing bonus for those who got an offer. One of my classmates applied and encouraged me to consider it. I asked “what do they do?”, “same kind of stuff we did last summer!”. We had a summer job working with PC’s we built from Popular Electronics and were writing word processing/formatting programs in Turbo Pascal on CP/M and tweaking motherboards with 8086 assembly language. “What? Work on those toys and they offer cash signing bonuses?” “No. Not cash, the signing bonus is 2,000 shares”. “What’s the company?” “It’s actually Micro-Soft, they’re in Albuquerque but the jobs are going to be in Seattle soon”.

Seattle? Ugh. Waaay over there on the rainy west coast, so far away. “No thanks. Aren’t they kind-of a sweat shop and shares aren’t publicly traded right?” “Not yet”. “Hmm… nah… pass”. My friend took the interview but didn’t get an offer. He was a top student, a great co-worker, and as far as I know nobody in our graduating class got an offer. Four years later “Micro-Soft” IPO'd as “MicroSoft” at $21 a share and thousands of millionaires and some billionaires were born.

Ralph Stanton and → Graduate School

WIthout a job offer, I decided to consider graduate school and at the time one needed a letter of recommendation from a professor. My natural choice was to attend the University of Waterloo as it provided good opportunities for employment as a grad student marking papers/exams, holding tutorials, etc. Also, one of my professors for undergraduate years was Professor Ralph Stanton, who was the founder of the University of Waterloo's Faculty of Mathematics.

He agreed to give me a recommendation, which I never read myself, he just said "I'll take care of it". I was accepted and felt relieved as I actually had financing and a job !

Ralph Stanton was a tough professor during 4 years at University of Manitoba. He was about as old school as you could be: never used a calculator, did iterations by hand to 5 decimals, always used something obscure involving number theory where solutions just popped out of nowhere, if we asked about it, he would say that “even a mentally deficient squirrel knows that”. His final exams were 80% or 100% of the course grade, no aids or notes allowed. If you could imagine a Professor Kingsfield from Paper Chase, but for mathematics, that would be him.

Stanton was, at times, brutal, many avoided his courses but despite their difficulty I rather enjoyed them because he was The Man, one of the greats, a real character, and without question an excellent teacher. Every one of his lectures was a new episode, a tour-de-force of mathematical stand-up improv, a consistent pedagogical style without notes or books.

Okay, more stories later, let’s get on to the proof.

The Problem:

(We can ignore the blue circles and the red line, they were part of the Sangaku problem)

Given a Circle \(O\) with radius \(R\) and and an oblique chord \(AC\) where the chord distance from \(O\)’s center is \(h\), express an equation for the line \(AC\) in terms of \(R\) and \(h\).

Overview of Proof:

Since this equation was used for a Sangaku discussion, we should really stay with the methods of the wasan of the Edo period who didn’t use trigonometric methods. For this proof we will have this outline:

1. Define equation for a line with \(Ax+By=C\), and use coordinates to give \(C\) in terms of \(A,R\).

2. Set conditions on \(h\) to define \(B(A,R,h)\)

3. Determine a value for \(A\) (!)

4. Substitute \(A, B, C\) in (1) and verify the equation for the chord.

Trigonometric methods are given at the end.

1) Define line equation and define coordinates to find \(C(A,R)\)

The equation for a line: \(Ax + By =C\)

Set circle center at \((0, 0)\). The chord is on \((R, 0)\), so

$$AR+B\cdot0=C \;\Rightarrow\; C = AR$$

2) Set conditions on \(h\) and solve for \(B(A,R,h)\)

The unsigned perpendicular distance \(d\) from \((x,y)\) to the line \(Ax+By=C\) is given by the standard formula, using \(C=AR\) from above:

$$d = \frac{|Ax + By - AR|}{\sqrt{A^2+B^2}}$$

For the distance \(d \) to origin, we set \((x,y)\) to \((0,0)\) and we have:

$$d = \frac{|0 + 0 - AR|}{\sqrt{A^2+B^2}} = \frac{AR}{\sqrt{A^2+B^2}}.$$

This distance we call \(h\) so substitute and solve for \(B\):

$$h = \frac{AR}{\sqrt{A^2+B^2}}$$

Reorganize:

$$\sqrt{A^2+B^2} = \frac{AR}{h}.$$

Square each side:

$$A^2+B^2 = \frac{A^2R^2}{h^2}.$$

$$B^2 = \frac{A^2R^2}{h^2} - A^2 = A^2\left(\frac{R^2 - h^2}{h^2}\right).$$

Take the positive square root and we have solved for \(B\):

$$B = A\frac{\sqrt{R^2-h^2}}{h}$$

3) Determine a value for \(A\) (!)

Here is something that Professor Stanton would do and raise everyone’s eyebrows.
We just choose a non-zero value for \(A\). We can just choose \(h\), since the only condition on \(A\) is that it must be non-zero, and \(h\) is definitely non-zero and positive.

So if we set

$$\text{(1)}\quad A = h$$

$$\text{(2)}\quad B = h\frac{\sqrt{R^2-h^2}}{h} = \sqrt{R^2-h^2}$$

and recall that \(C=AR\): then we have:

$$\text{(3)}\quad C = hR$$

4) Substitute and verify:

So we have the equations for \(A, B, C\) in terms of \(h \) and \(R\). Now just substitute them into the general line equation and verify.

$$Ax+By=C$$

$$\Rightarrow\quad hx+(\sqrt{R^2-h^2})y=hR\quad\text{(4)}$$

1. Verify that it passes through \((R, 0)\), substituting \((x,y) \) with \((R,0)\): \(\boxed{hR = hR}\)

2. Verify that the distance from origin is \(h\), ensuring the algebra above was correct, reversing the process to get the same result.

Use the formula of distance from a point to a line,
where the point is \((0,0)\)and the line is equation \(\text{(4)}\)

$$\frac{|h\cdot0 + \sqrt{R^2-h^2}\cdot 0 - hR|}{\sqrt{h^2+ (R^2-h^2)}} = \frac{hR}{\sqrt{R^2}} = \frac{hR}{R} = \boxed{h}.$$

Thus, the equation of a chord with height \(h\) from circle center with radius \(R\), passing through \((R,0)\)is:

$$\boxed{hx + \sqrt{R^2-h^2}\,y = hR.}$$

Using Trigonometric Methods:

The trigonometric method is far less cumbersome. I’ll be brief here in the style of Professor Stanton, “any other details will be left for the student”

Define the chord in polar form: \(x\cos\alpha + y\sin\alpha = h\). With the chord passing through \((R,0)\) we have:

$$\text{(1)}\quad R\cos\alpha +0\cdot\sin\alpha = h \; \Rightarrow\; R\cos\alpha=h\; \Rightarrow\;\cos\alpha=\frac{h}{R}$$

Using \(\sin^2\alpha+\cos^2\alpha=1\) we have:

$$\text{(2)}\quad \sin\alpha=\sqrt{1-\cos^2\alpha} = \sqrt{1-\left(\frac{h}{R}\right)^2} = \frac{\sqrt{R^2-h^2}}{R}$$

Substitute \(\text{(1)}\)and \(\text{(2)}\) into the polar form above:

$$x\left(\frac{h}{R}\right) + y\frac{\sqrt{R^2-h^2}}{R} = h$$

$$\Rightarrow \boxed{hx + \sqrt{R^2-h^2}y = hR}$$

Conclusion:

Had this been one of Professor Stanton’s lectures he would have taken about two minutes on the blackboard, with many steps just skimmed over, and then everything would be promptly erased.

While I was at UofM Professor Stanton lobbied to create a “School of Computer Science” (see the tshirt in yellow above) but his dream fell flat. There wasn’t any other “school” in the Faculty of Science at the time, and there was great objection from the Head of the Department of Mathematics, Nathan Mendelsohn. I remember going to a meeting where Prof. Mendelsohn rambled on and on about how “computer science was not so special to be a separate school”, it was quite a heated debate.

But there was no question that the Computer Science department had character and identity at UofM. We were the social ones that held Donuts and Coffee hours, occupied the Top Floor of Macray Hall, had a “swamp” ala M*A*S*H which the occupiers called Ouagadougou, and we had a very special annual event called “The Ralphies” (see the red t-shirt above) where we celebrated the man with the pink tie, the founder of the Faculty of Mathematics at UofW, and our Computer Science and Mathematics leader.

After I graduated I found out that Prof. Stanton was the most prolific donor to the Fisher Library. His first donation was an original 1587 2nd edition of the Holinshed Chronicles, the actual volumes that were used by Shakespeare as the basis of many of his plays. Today an original is worth almost $30,000! That donation was in 1986 and for the next 14 years until his death he donated many significant works. While we learned much mathematics from him we did not know much about the Renaissance Man that he was.