Verifying ECDSA signatures
 Andrej
Andrej
I am not going to give a full introduction to Elliptic Curve Cryptography or ECDSA because there are much better resources on the topic. I personally find this blog post series to be one of the greatest explanations online. I highly recommend checking it out to better understand this article.
Preface
The Ethereum blockchain uses the secp256k1 elliptic curve over a finite field p. Ethereum transactions are cryptographically signed using the Elliptic Curve Digital Signature Algorithm (ECDSA). Assuming Alice’s private key is not compromised, when Alice signs a transaction using her private key, Bob, as the recipient, can verify that signature against Alice’s public key and be sure that the transaction came from Alice. That’s what digital signatures are for, in general.
Warm-up example
If you want to execute this process on your machine, make sure you have OpenSSL installed and follow the next steps.
Step 1) Generate a random private key for the secp256k1 elliptic curve. The new private_key.pem file will be generated.
The private key is nothing but a randomly selected 256-bit integer. If we flip the coin 256 times and write down 0 or 1 depending on whether the coin landed on the “head” or “tail”, we can probably generate a private key that no one else uses. Obviously, you should use stronger entropy than flipping a coin, but that’s the essence of the process. Usually that entropy is mapped to a set of words from a predefined wordlist that allows you to securely back up and recover your private key(s), also known as a 24-word seed phrase or mnemonic phrase. I won’t be getting into it in this article - if you are interested, read the BIP-39 standard.
openssl ecparam -name secp256k1 -genkey -noout -out private_key.pem
If you want to see the private key in the hex format we are all used to, you can optionally run the following command.
openssl ec -in private_key.pem -noout -text | grep 'priv:' -A3 | tail -3 | tr -d ':\n ' | sed 's/priv//g'
Step 2) Calculate the corresponding public key using the previously generated private key. The new public_key.pem file will be generated.
The public key is calculated by performing an elliptic curve scalar multiplication of the private key with the secp256k1 curve's publicly known generator point (G): Public Key = Private Key * G. Due to the elliptic curve discrete logarithm problem, it is infeasible to derive the private key from the public key, which is why it is safe for Alice’s public key to be publicly known by anyone.
If the previous two sentences sound incomprehensible, don’t worry, I’ll explain the concept briefly. For a full explanation revisit the material linked in the introduction of this article. Imagine you get the prime number 190 549 069, a product of two numbers, and you need to find those two numbers. This would be a difficult and time-consuming operation without some prior knowledge. The discrete logarithm problem is like trying to figure out what the original number was just by knowing it and how it was generated (multiplication of two numbers in our example). Now, if I tell you that one of the numbers was 12347, the computation of the second one becomes trivial.
openssl ec -in private_key.pem -pubout -out public_key.pem
If you want to (optionally) calculate Alice’s Ethereum address from this public key, hash it using the keccak256 algorithm and get the last 20 bytes of that hash.
Step 3) Create a publicly visible message for Alice to send to Bob. Remember, the purpose of this exercise is for Bob to validate that the message received was signed and sent by Alice. In production, however, you must always hash the message content.
echo "This is example" > message.txt
Step 4) Digitally sign the message.txt file using Alice’s private key. The new signature.bin file will be generated.
openssl dgst -keccak-256 -sign private_key.pem -out signature.bin message.txt
Step 5) Send both message.txt and signature.bin files to Bob. Verify that the message was signed with Alice’s private key, using her public key. You will either see the “Verified OK” or “Verification Failure” output.
openssl dgst -keccak-256 -verify public_key.pem -signature signature.bin message.txt
A brief intro to the secp256k1 elliptic curve
An elliptic curve is nothing but a set of points described by the equation:
$$y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0$$
To transform it into an elliptic curve over a finite field p, we just need to introduce a prime number p and perform modular arithmetic over it. So essentially, the secp256k1 elliptic curve over a finite field p is the set of possible points defined by just three integers:
a = 0
b = 7
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
So the equation now becomes:
$$y^2 = x^3 + 7 \pmod p$$
And Alice’s public key is just one of those points. To validate whether a point is valid on the secp256k1 curve, you can use this simple Python script:
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
def isValidPointOnSecp256k1Curve(point):
x = point[0] % p
y = point[1] % p
return (y ** 2) % p == (x ** 3 + 7) % p
Then, you can test this script with a random invalid point x = 10, y = 2, and a known valid point G (Generator).
if __name__ == '__main__':
# Test against a random invalid point, prints False
print(isValidPointOnSecp256k1Curve([10, 2]))
# Test against a known valid point (Generator), prints True
print(isValidPointOnSecp256k1Curve([0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8]))
These numbers are really big, making visualizing the curve hard. However, if we “scale” it to a smaller finite field using 17 as p, the curve looks like this (the below screenshots are from https://andrea.corbellini.name/ecc/interactive/modk-mul.html):
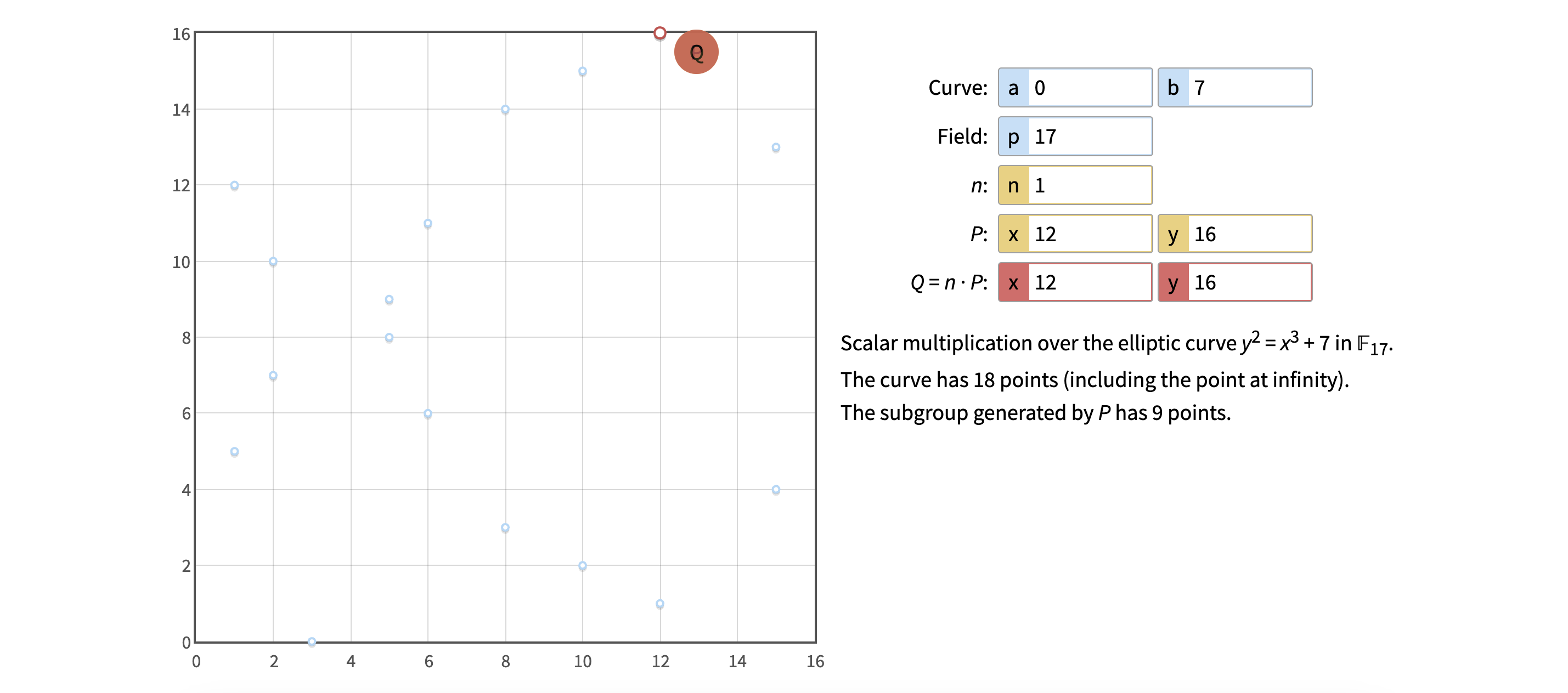
If we set p to 23, it looks like this:
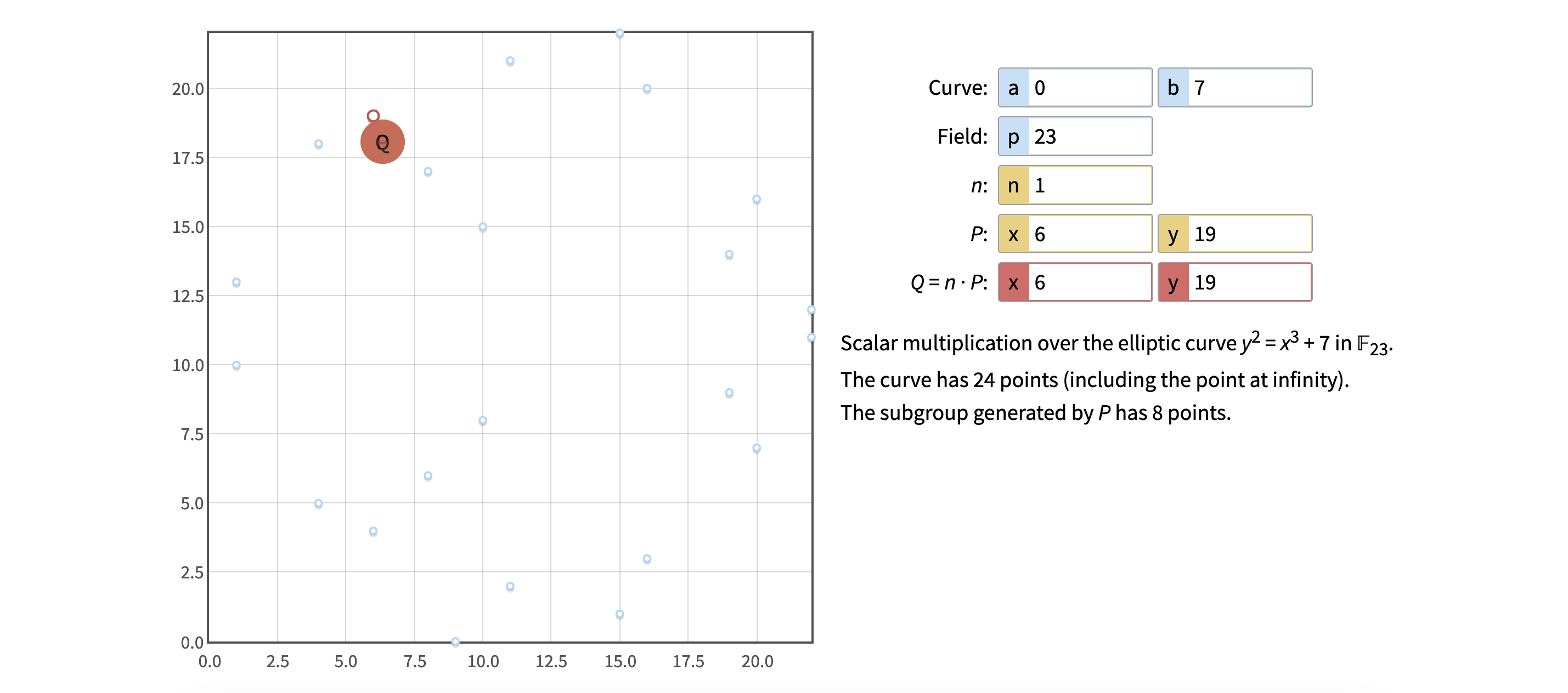
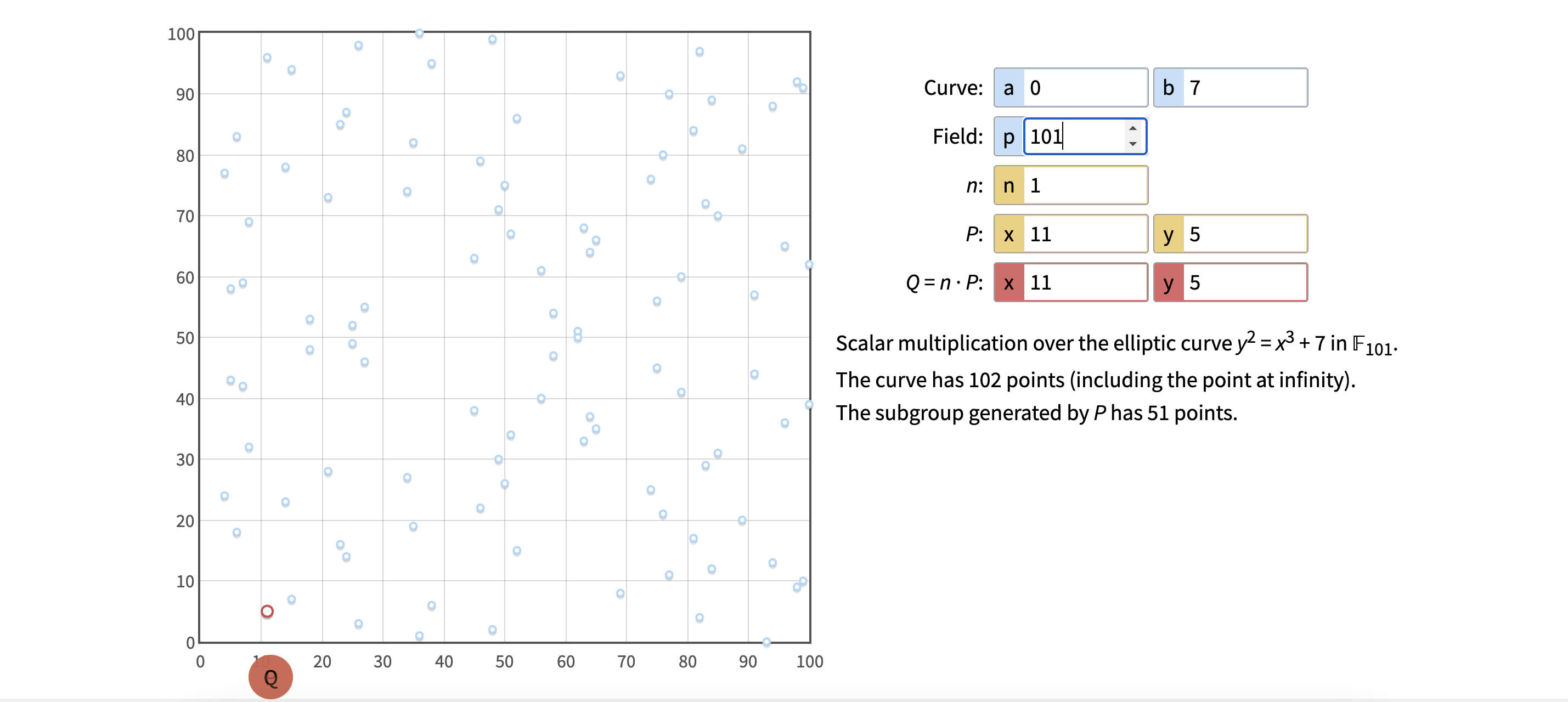
Or if we set p to 101, it looks like this:
If we look closer, we will notice one of this curve's two important properties: it is symmetric along the y-axis!
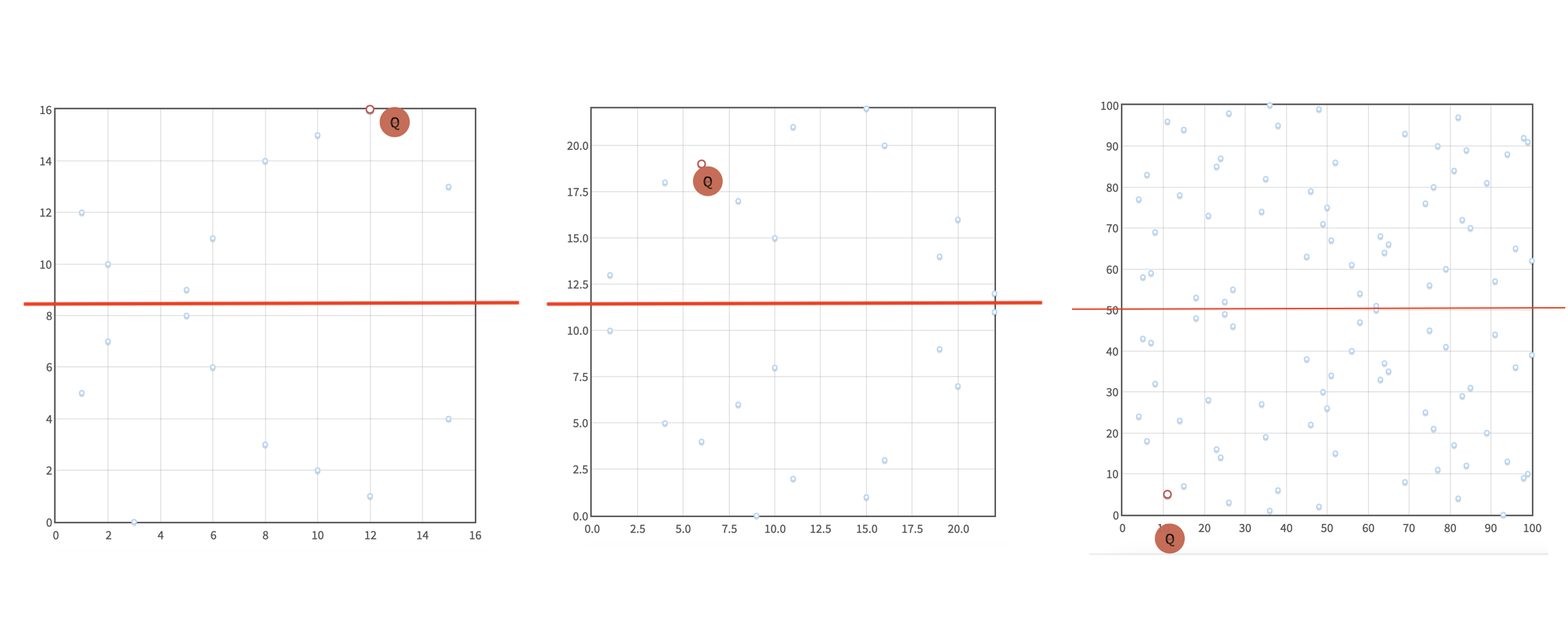
The second important property of this curve is cyclic subgroups!
If we again take a look at the curve where a = 0, b = 7 and p = 23, and pick G(6, 19) as the Generator point (marked as P on the image), we might notice the following if we start calculating all the multiplies of G.

0 * G = 0 (a.k.a point in infinity)
1 * G = (6, 19)
2 * G = (15, 22)
3 * G = (20, 7)
4 * G = (9, 0)
5 * G = (20, 16)
6 * G = (15, 1)
7 * G = (6, 4)
8 * G = 0 (a.k.a point in infinity)
9 * G = (6, 19)
10 * G = (15, 22)
11 * G = (20, 7)
…
We notice that only 8 possible points appear and that they are repeated cyclically.
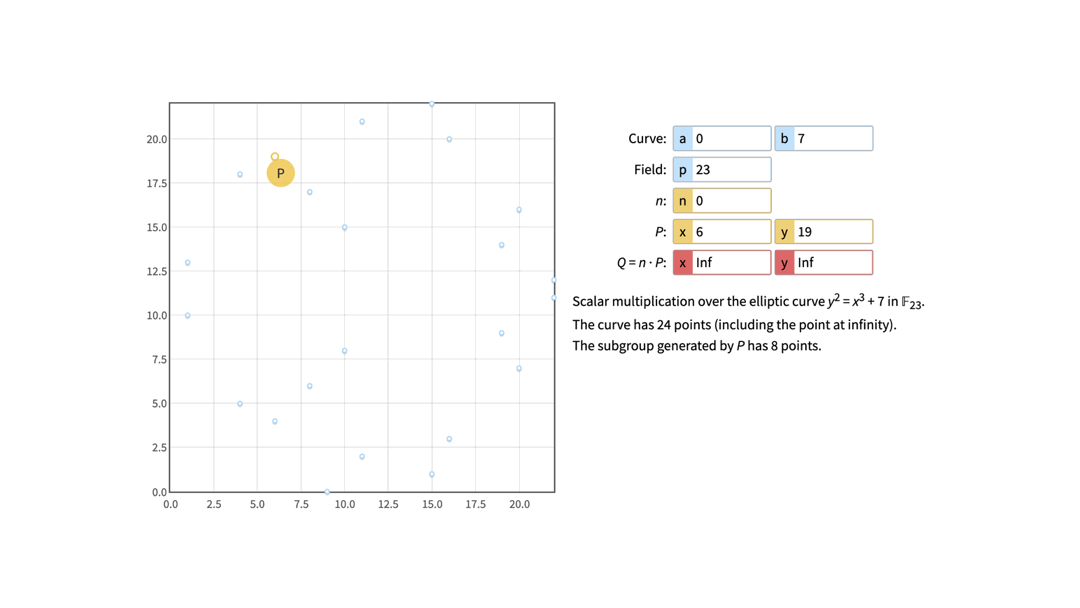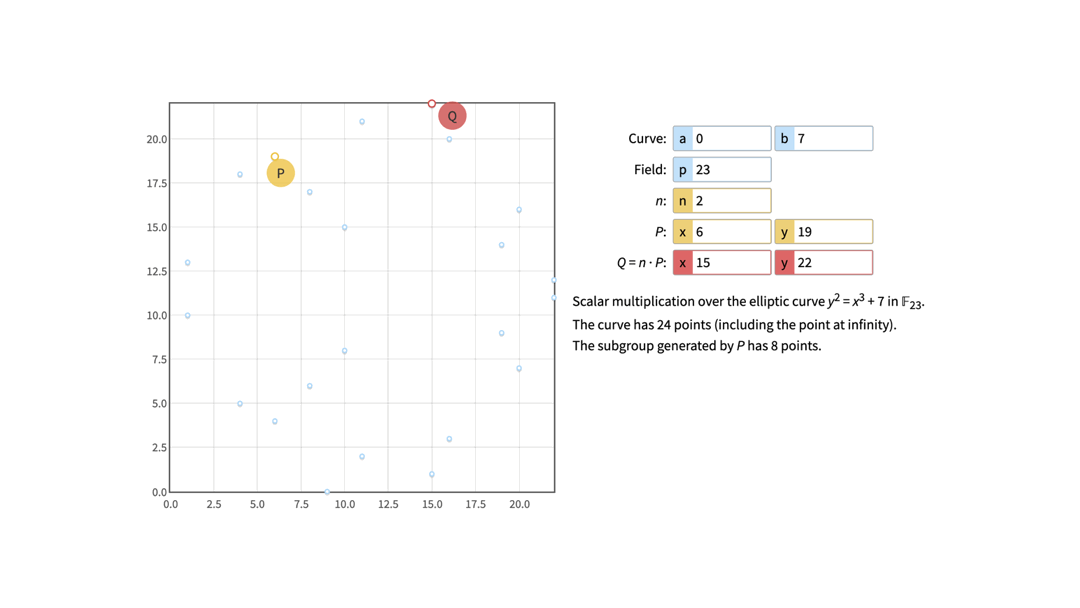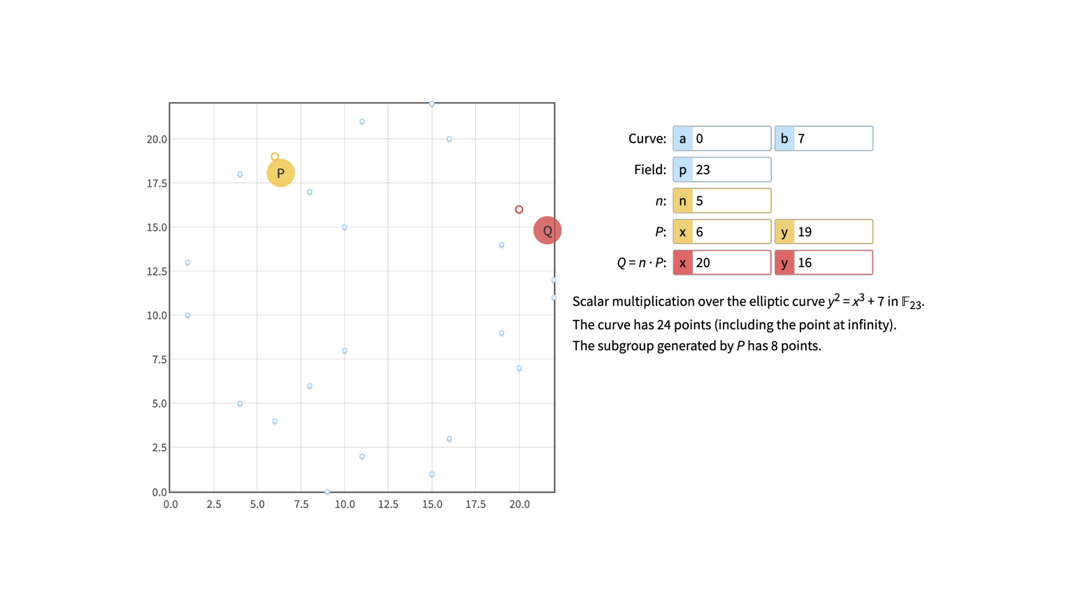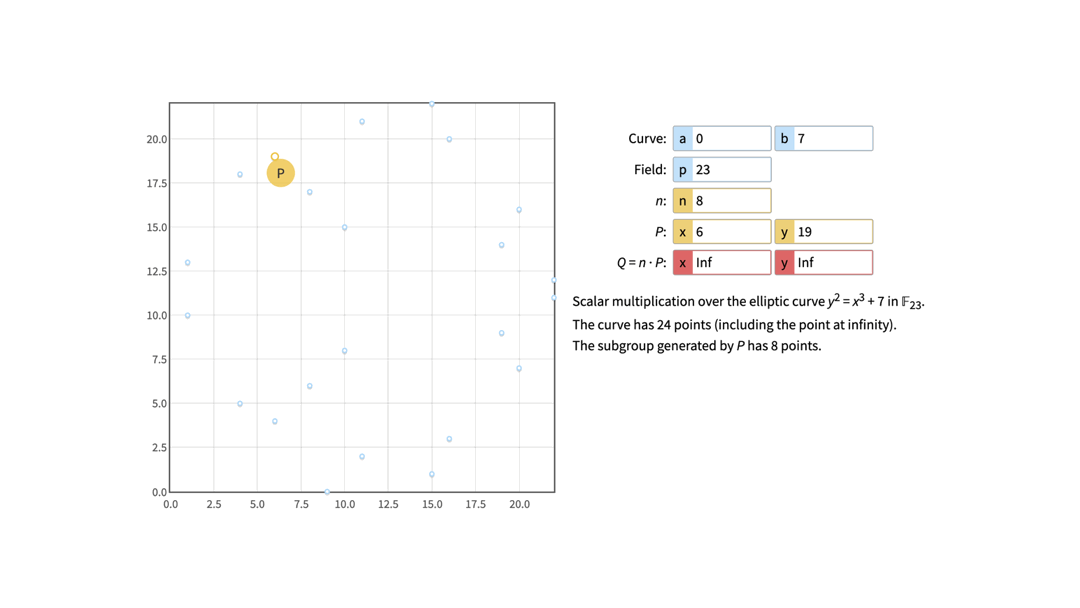
This means that if we now say the private key is, for example, number 9, we can easily calculate that the corresponding public key is Q(6, 19) because Q = 9 * G. However, it is difficult and time-consuming to calculate the private key from the given public key (6, 19) - is it 1, 9, 17, etc.? This is the discrete logarithm problem.
And if we imagine the elliptic curve as a looped track, the Generator point is like the start line.
We noticed earlier that only 8 points were repeated cyclically, even though the curve itself has 24 points (p = 23 + the point at infinity). The p prime number we were changing from 17 to 101 represents the size of the curve - notice how when p was 17, the curve had 18 points in total (17 points + the point at infinity), when p was 101 the curve had 102 points in total (101 points + the point at infinity), and so on. So why were there only 8 points repeated cyclically?
That number 8 is the order n of a subgroup generated by a Generator point G. In fact, it is the smallest positive integer such that n * G = 0. It is really important that the order n is the smallest divisor, not a random one, and that the order n is a prime number - otherwise, ECDSA won’t work.
Number 8 is obviously not a prime number, so our minimalistic curve can’t be used for generating ECDSA signatures. Still, this example helped us understand all the parameters of the secp256k1 elliptic curve, except for the cofactor of the subgroup h, which won’t be needed throughout the rest of the article. However, I highly encourage you to read the linked blog post series from the beginning to understand the role of h.
To sum up, the secp256k1 elliptic curve over a finite field p is the set of possible points defined by:
a = 0
b = 7
p (size of the curve) = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
G (generator point - the start line of a “looped track”) -
(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)n (order) - 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h - 1
Working with ECDSA signatures on Ethereum
When working with ECDSA signatures signed by Externally Owned Accounts, essentially, there are just two steps:
Users sign some messages using their private keys
Your smart contract uses ecrecover precompile (
address(0×01)on Ethereum) to recover the public key from that signature and then perform certain actions
Signing the message
The first step is to compute the keccak256 hash of the message content. The second is to call the sign method, which will return variables v,r, and s. In Foundry, that would look something like this:
bytes32 digest = keccak256(abi.encodePacked("Hello, world!"));
(uint8 v, bytes32 r, bytes32 s) = vm.sign(alicePrivateKey, digest);
This vm.sign function will choose the random number k such that 1 ≤ k < n, where n is the order of the elliptic curve's Generator point G. The same thing your wallet’s implementation or ethers.js will do, for example.
Then, it will calculate the point R(x₁, y₁) on the curve by multiplying k with the Generator point G. Following our analogy with the elliptic curve as a looped track, the signer will run k laps around the track ending at point R. Finally, the vm.sign function will calculate and return the variable r, as r = x₁ mod n, where x₁ is the x-coordinate of the point R = k * G.
Generally, users do not choose or have influence over number k. But it is critical that k remains private, used only once and its random number generator is not predictable. Otherwise, if there are two signatures generated using the same publicly known number, k, it is possible to derive the user’s private key from the r and s values and hashed message contents of those two signatures. To solve this problem, the RFC 6979 standard was created. It specifies a method for generating the “ephemeral nonce k in a deterministic manner during the digital signature process, specifically for DSA and ECDSA algorithms”, and it is being widely used among different library implementations.
So the random k value was picked, the signer ran k laps around the track and ended at some point R. That is yet another point on the curve - do not confuse it with the Generator point or your public key. From point R, the r value was derived. What about s and v?
The s value serves as cryptographic proof that the signature is uniquely linked to both the specific message and the signer's private key. It is calculated using the following formula:
$$s = k^{−1} (messageHash + r⋅privateKey) \pmod n$$
Imagine the value s as a personalized stamp or signature that the runner leaves at the finish line. It combines the runner's identity (private key), the message hash being signed, and the number of laps run (k). Later, it will play a crucial role for the Verifier to determine whether a signature is valid without knowing the signer's private key or public key.
Finally, speaking of value v, remember how the secp256k1 curve is symmetrical along the y-axis. That means when the signer arrives at the point R(x₁, y₁), there is a symmetrical point R(x₁’, y₁’) on the other side of the y-axis. If the value v is 27 (or 0 in some implementations), the point R is in the lower part of the curve. If the value v is 28 (or 1 in some implementations), the point R is in the upper part of the curve.
Recovering the public key from the signature
Once we have a signature, our smart contract should use the ecrecover precompile (address(0×01) on Ethereum) to recover the public key from that signature and then perform certain actions. Throughout the rest of the article we will focus on designing smart contracts to handle verification of signatures correctly. Numerous use cases and advanced Solidity patterns are possible with ECDSA signatures - from gasless transactions to NFT “lazy minting”.
The naive implementation would look something like this. Do not use this code in production, because a lot of stuff could go wrong.
function verifySignature(bytes32 hash, uint8 v, bytes32 r, bytes32 s)
external
view
returns (bool, address)
{
address recoveredAddress = ecrecover(hash, v, r, s);
return (recoveredAddress != address(0), recoveredAddress);
}
We will now analyze what the ecrecover precompile does on a conceptual level. It uses the r, s, and v values to recover the signer’s public key without knowing the signer's private key or public key in advance. Then, it calculates the signer’s Ethereum address by computing the keccak256 hash of the recovered public key and obtaining the last 20 bytes of that hash. Finally, it returns either that Ethereum address or address(0).
From the r value, it reconstructs possible points R.
Then, it calculates the signer’s public key using the following formula, effectively reversing the signing process (picking up the signature the signer left at the finish line and reconstructing the runner's path from the recovered point R):
$$publicKey = r ^ {−1} (s⋅R − messageHash⋅G)\pmod n$$
The value v helps speed up the verification process because it tells the Verifier which of the two symmetrical points R to use in the formula for calculating the signer’s public key. If Alice tells Bob that v = 27 (meaning the point R is in the lower part of the curve), and Bob calculates the public key, which is indeed Alice’s public key, Bob can be more confident that Alice signed that message with her private key because Alice knew at which point R she arrived after running k laps.
For a given r, s, and messageHash, there are multiple potential public keys. With v, the Verifier doesn't have to test all possible keys, speeding up the recovery process.
Handling invalid signatures
A couple of libraries are specifically designed to help verify ECDSA signatures on-chain. I will still explain how you can verify ECDSA signatures without external dependencies, but I highly recommend using OpenZeppelin’s ECDSA.sol since that is a more secure and faster solution. That library is already audited and battle-tested in a production environment.
ECDSA signatures signed by Externally Owned Accounts usually have a fixed length of 65 bytes.
To reduce gas costs and transaction sizes, the compact representation of the ECDSA signature was designed in the EIP-2098. Those compact signatures have a fixed length of 64 bytes.
This means that if a signature is not 65 or 64 bytes long, your verifier contract should throw an error.
error InvalidSignatureLength();
function verify(
bytes calldata signature,
bytes32 messageHash
) internal pure {
bytes32 r;
bytes32 s;
uint8 v;
if (signature.length == 65) {
// Handle regular ECDSA signatures
} else if (signature.length == 64) {
// Handle compact ECDSA signatures
} else {
revert InvalidSignatureLength();
}
}
In standard EDCSA signature representation, the value r is stored in the first 32 bytes, s is stored in the next 32 bytes, and the last byte represents the value v. Decoding the signature for further usage is trivial.
error InvalidSignatureLength();
function verify(
bytes calldata signature,
bytes32 messageHash
) internal pure {
bytes32 r;
bytes32 s;
uint8 v;
if (signature.length == 65) {
(r, s) = abi.decode(signature, (bytes32, bytes32));
v = uint8(signature[64]);
} else if (signature.length == 64) {
// Handle compact ECDSA signatures
} else {
revert InvalidSignatureLength();
}
}
In compact ECDSA signature representation (EIP-2098), to lower gas costs, the value r is stored in the first 32 bytes, and in the next 32 bytes, the values v and s are stored together with the value v stored in the highest bit of that compact representation.
Decoding the r value is trivial.
The line s = vs & UPPER_BIT_MASK; extracts the s value by applying a "bit-mask" that keeps all bits except the highest one (the value v). How?
A “bit-mask” is a pattern of bits used to selectively manipulate (keep, remove, or flip) specific bits within a binary number through bitwise operations like AND, OR, XOR, etc.
In Solidity, the & syntax represents the AND operator. The AND operator compares two binary numbers bit by bit and produces a result where:
If both bits are 1, the result is 1
If either bit is 0, the result is 0
| X | Y | AND |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Let’s say we want to apply the AND operator to binary numbers 0111 1111 and 1111 1010.
0111 1111
& 1111 1010
—————
0111 1010
The end result is the value 0111 1010 which is the initial value 1111 1010 except the highest bit, which became 0. In this example, the value 0111 1111 served as a “bit-mask” that cleared the highest bit while preserving all other bits. This elegant approach lets you isolate and extract specific components from packed data structures.
In the context of our code, the UPPER_BIT_MASK hex value 0x7fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff is 0111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 in binary. The first digit is 0 (the most significant bit) while the remaining 255 bits are all 1s.
Using this “bit-mask” one can extract the s value from the compact signature representation by removing the v value stored in the highest bit.
Let’s now break down the following line: v = uint8(uint256(vs >> 255)) + 27;
First, let’s analyze the vs >> 255 part. The >> in Solidity represents the right shift operator that shifts the given value right by N positions. With each shift to the right, new zero bits are filled in from the left. For example, let’s shift the 1100 1100 value right by 7 positions (11001100 >> 7).
Start: 1100 1100
Step 1: 0110 0110 (shift right by 1)
Step 2: 0011 0011 (shift right by 2)
Step 3: 0001 1001 (shift right by 3)
Step 4: 0000 1100 (shift right by 4)
Step 5: 0000 0110 (shift right by 5)
Step 6: 0000 0011 (shift right by 6)
Step 7: 0000 0001 (shift right by 7)
In the context of our code, the vs >> 255 part will shift the compact signature representation right by 255 positions, effectively unpacking the v value, and discarding all other bits. The result will be either 0 or 1.
However, the ecrecover precompile expects the v value to be either 27 (if v was 0) or 28 (if v was 1), which will be explained later in the article, and because of that we need to add 27 to the previously extracted bit v.
error InvalidSignatureLength();
bytes32 constant UPPER_BIT_MASK = (0x7fffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff);
function verify(
bytes calldata signature,
bytes32 messageHash
) internal pure {
bytes32 r;
bytes32 s;
uint8 v;
if (signature.length == 65) {
// Handle regular ECDSA signatures
} else if (signature.length == 64) {
bytes32 vs;
(r, vs) = abi.decode(signature, (bytes32, bytes32));
s = vs & UPPER_BIT_MASK;
v = uint8(uint256(vs >> 255)) + 27;
} else {
revert InvalidSignatureLength();
}
}
In this article, we won’t cover handling EIP-1271 signatures. The code snippets assume that the account calling the verify function is the signer of the given signature which might not always be the case.
Finally, after handling standard and compact ECDSA representations, we can interact with the ecrecover precompile.
error InvalidSignatureLength();
error InvalidSignature();
error InvalidSigner();
function verify(
bytes calldata signature,
bytes32 messageHash
) internal pure {
bytes32 r;
bytes32 s;
uint8 v;
if (signature.length == 65) {
// Handle regular ECDSA signatures
} else if (signature.length == 64) {
// Handle compact ECDSA signatures
} else {
revert InvalidSignatureLength();
}
address signer = ecrecover(messageHash, v, r, s);
if (signer == address(0)) revert InvalidSignature();
if (msg.sender != signer) revert InvalidSigner();
}
Prevent front-running
Let’s imagine that we want to create a smart contract that integrates an IoT device to lock or unlock a door in your home. When you provide a valid signature, the contract should emit an event that unlocks the door for the authorized controller.
The challenge is that the user’s signature will be visible in the mempool as part of the transaction’s calldata. Malicious users can front-run this transaction and use this valid signature to unlock the door.
To prevent front-running, make sure that you validate the “ecrecovered” address against the msg.sender.
And if you want to play more with smart contracts for unlocking doors with IoT devices, you can check out level 32 of the Ethernaut CTF: Impersonator.
error InvalidSigner();
function verify(
bytes calldata signature,
bytes32 messageHash
) internal view {
bytes32 r;
bytes32 s;
uint8 v;
// handling invalid signatures logic here
address signer = ecrecover(messageHash, v, r, s);
if (msg.sender != signer) revert InvalidSigner();
}
EIP-191
It’s easy to trick someone into signing some malicious data, such as draining all of the native coins (ETH for Ethereum) from a victim’s account. To prevent this from happening, the EIP-191 standard was introduced. It requires message data that needs to be signed (before hashing) to be in a certain format, as described in the table below.
| Version byte | EIP | |
| 0×00 | EIP-191 | 0×19<0×00><validator_address><data_to_sign> |
| 0×45 | EIP-191 | 0×19<0×45(E)><thereum Signed Message:\n + len(message)><data_to_sign> |
In the ASCII table, the capital letter “E” has a hexadecimal value of 0×45.
Signature malleability
In the “Recovering the public key from the signature“ section, we mentioned that for a given r, s, and messageHash, there are multiple potential public keys due to the symmetrical nature of the secp256k1 elliptic curve over a finite field p.
In practice, this means that for any given valid ECDSA signature, the symmetrical one can be easily computed. The problem is that ecrecover precompile won’t revert if you attempt to use that symmetrical one. Instead, it will return some address (not even address(0)) that’s not the address of the original signer. This is another reason why you should validate the “ecrecovered” address against the msg.sender or the signer provided as a function argument.
To address this issue, the EIP-2 was proposed. It states that only the lower s value of the signature is considered valid. However, this change was never implemented in the ecrecover precompile, leaving smart contract developers responsible for handling malleable signatures. To do that, you must reject signatures where:
s is in the upper half of the curve
v is not 27 or 28
We already mentioned that the Curve Order (N) of the secp256k1 elliptic curve is 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141. To determine whether the s value is in the upper or lower half of the curve, we just need to compute the half of the Curve Order (N), which is the following value 0x7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF5D576E7357A4501DDFE92F46681B20A0. Now, in your smart contract, you just need to throw an error if the s value is greater than half of the Curve Order (N).
What about the v value? Most implementations of signing libraries will produce signatures with the v value equal to either 0 or 1. However, the ecrecover precompile expects these values to be either 27 or 28, as you can see here and here for geth, and here and here for reth. That’s the reason why you might need to upcast the v value in your smart contract.
The v value is also known as recid, and we said its purpose is to speed up the verification process since it represents the “number of hops to the key”. Here’s the cheat sheet on all possible v values taken from here.
| 27 | uncompressed public key, y-parity 0, magnitude of x lower than the curve order |
| 28 | uncompressed public key, y-parity 1, magnitude of x lower than the curve order |
| 29 | uncompressed public key, y-parity 0, magnitude of x greater than the curve order |
| 30 | uncompressed public key, y-parity 1, magnitude of x greater than the curve order |
| 31 | compressed public key, y-parity 0, magnitude of x lower than the curve order |
| 32 | compressed public key, y-parity 1, magnitude of x lower than the curve order |
| 33 | compressed public key, y-parity 0, magnitude of x greater than the curve order |
| 34 | compressed public key, y-parity 1, magnitude of x greater than the curve order |
| \>= 35 | potentially EIP-155 signatures |
Here’s how you can prevent signature malleability in your smart contract.
error InvalidSigner();
error InvalidValueS();
error InvalidValueV();
uint256 constant N_2 = 0x7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF5D576E7357A4501DDFE92F46681B20A0;
function verify(
bytes calldata signature,
bytes32 messageHash
) internal view {
bytes32 r;
bytes32 s;
uint8 v;
// handling invalid signatures logic here
if (uint256(s) > N_2) revert InvalidValueS();
if (v != 27 && v != 28) revert InvalidValueV();
address signer = ecrecover(messageHash, v, r, s);
if (msg.sender != signer) revert InvalidSigner();
}
You would obviously want to write some tests to ensure that your smart contract implementation is not vulnerable to signature malleability. Here’s how you can generate a symmetrical malleable signature in Solidity. You need to calculate the s₁ value by adding the N_2 value (0x7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF5D576E7357A4501DDFE92F46681B20A0) to the original s value. You will then flip the v value - if it was 27, it should become 28, and vice versa.
function test_signatureMalleability() public {
assertNotEq(alicePrivateKey, bobPrivateKey);
// ERC-191 signed data
bytes32 digest = keccak256(abi.encodePacked("Hello, world!")).toEthSignedMessageHash();
// secp256k1 Curve Order (N)
uint256 N = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141;
// N / 2 (to prevent signature malleability s <= N / 2)
uint256 N_2 = 0x7FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF5D576E7357A4501DDFE92F46681B20A0;
assertEq(N / 2, N_2);
vm.startPrank(alice);
(uint8 v, bytes32 r, bytes32 s) = vm.sign(alicePrivateKey, digest);
vm.stopPrank();
vm.startPrank(bob);
// Bob sees the signature in the mempool and computes the mirror signature
uint8 v1 = v == 27 ? 28 : 27;
bytes32 s1 = bytes32(uint256(s) + N_2);
(bool success, address recoveredAddress) = victim.verifySignature(digest, v1, r, s1);
vm.stopPrank();
if (success == true) {
console.log("Your contract is vulnerable to signature malleability :)");
}
}
EIP-712
Designing applications that utilize signatures is challenging because it is difficult for Users to understand what they are signing, which can lead to phishing and similar attacks. EIP-712 introduces a standardized way to sign data, ensuring that Users see human-readable messages before signing transactions. This reduces the risk of fraudulent activities and improves developer experience.
The EIP-712 standard consists of three pillars:
Domain Separator
Struct Hash
Final EIP-712 Hash leveraging the EIP-191 standard
Domain Separator
It is popular for cross-chain applications to deploy smart contracts to the same addresses in order to improve user experience. Using Domain Separator prevents cross-chain replay attacks.
Domain Separator ensures that signatures are utilized only on a proper chain for a given contract address. It was originally introduced because of the Ethereum Classic, but it became far more useful with the rise of Layer 2s.
The latest version of the EIP-712 Domain (V4) has the following fields:
string name- dApp name. For example, Uniswapstring version- dApp version. For example, V2uint256 chainId- The EIP-155 Chain ID which helps in preventing cross-chain replay attacks. For example, 1 for Ethereum Mainnet or 137 for Polygon Mainnetaddress verifyingContract- The address of a smart contract that will verify the signature for a given action - this is a contract we are designing.bytes32 salt- If the previous four fields can’t uniquely distinguish the application, this field can be used as a last resort. Note that OpenZeppelin’s implementation, at the moment of writing this article, did not utilize this field.
To construct the Domain Separator V4, you first need to calculate the bytes32 TYPE_HASH which is the keccak256 hash of the string of the EIP-712 Domain.
bytes32 constant TYPE_HASH = keccak256("EIP712Domain(string name,string version,uint256 chainId,address verifyingContract,bytes32 salt)");
Next, you need to encode the given TYPE_HASH with the actual values and finally apply the keccak256 hash to everything.
bytes32 constant TYPE_HASH = keccak256("EIP712Domain(string name,string version,uint256 chainId,address verifyingContract,bytes32 salt)");
function domainSeparatorV4() public view virtual returns (bytes32) {
return keccak256(
abi.encode(
TYPE_HASH, keccak256(bytes("MyDapp")), keccak256(bytes("1")), block.chainid, address(this), ""
)
);
}
Struct Hash
Struct Hash ensures that the signature may be only used for specific purposes. You can have multiple struct hashes in a single contract.
For example, you can allow signing invoices defined with the following struct:
struct Invoice {
uint256 id;
address payer;
uint256 amountDue;
uint256 deadline; // Deadline timestamp, to be explained later
uint256 nonce; // This can be used to prevent replay attacks, to be explained later
}
Or signing emails defined with another struct:
struct Email {
address to;
string message;
}
Or signing ERC-20 Permits (to grant gasless approvals) with another struct. Etc, etc.
struct Permit {
address owner;
address spender;
uint256 value;
uint256 deadline;
uint256 nonce;
uint8 v;
bytes32 r;
bytes32 s;
}
Then you will need to create the appropriate typehash. For the Invoice struct, it will look like this:
bytes32 constant INVOICE_TYPEHASH = keccak256("Invoice(uint256 id,address payer,uint256 amountDue,uint256 deadline,uint256 nonce)");
To finally form a Struct Hash that Users will generate and sign off-chain. Remember, this code should not be part of your smart contract; this is an off-chain action.
In Foundry, that would look something like this:
bytes32 structHash = keccak256(abi.encode(INVOICE_TYPEHASH, _id, _payer, _amountDue, _deadline, _nonce));
Final EIP-712 Hash
As mentioned before, this part leverages the EIP-191 signed data standard to define a version number and version-specific data. It must start with 0×19 as a prefix, followed by 0×01 as version byte to indicate this is an EIP-712 signature:
function hashTypedDataV4(bytes32 structHash) internal view returns (bytes32) {
return keccak256(abi.encodePacked("\x19\x01", domainSeparatorV4(), structHash));
}
Off-chain, you will let Users sign the data using Metamask’s eth_signTypedData_v4, ethers V6’s signer.signTypedData, or another method. The important thing is that whatever is signed off-chain must exactly match the output of the hashTypedDataV4(bytes32 structHash) on-chain function described above.
How EIP-712 differs from EIP-191?
We already mentioned that the EIP-191 standard requires message data that needs to be signed (before hashing) to be in a certain format, with either 0×00 or 0×45 version bytes. If the version byte is 0×01 however, that means we are dealing with the EIP-712 signature.
| Version byte | EIP | |
| 0×00 | EIP-191 | 0×19<0×00><validator_address><data_to_sign> |
| 0×01 | EIP-712 | 0×19<0×01><domainSeparatorV4><structHash> |
| 0×45 | EIP-191 | 0×19<0×45(E)><thereum Signed Message:\n + len(message)><data_to_sign> |
Most function implementations for signing off-chain messages leverage the eth_sign method from the Ethereum JSON RPC API. Historically, it used to encrypt messages with the User's private key and return the raw bytes data. Signing such data is risky because most Users are not aware of what they are signing. That implementation is mostly deprecated in favor of the method that calculates an Ethereum-specific signature with: sign(keccak256("\x19Ethereum Signed Message:\n" + len(message) + message)).
Metamask, on the other hand, still kept the original, deprecated implementation, but it keeps it disabled by default. Instead, they introduced the personal_sign method specific to their API. In the ethers V6 library, the eth_sign is merged with personal_sign into the signer.signMessage method. In Foundry, the call to the eth_sign method from the Ethereum JSON RPC API is triggered from the vm.sign function.
Here’s the full breakdown:
| EIP-191 | EIP-712 | |
| Metamask | personal_sign | eth_signTypedData_V4 |
| Ethers V6 | signer.signMessage | signer.signTypedData |
| Foundry | bytes32 digest = keccak256(abi.encodePacked(message)).toEthSignedHash(); vm.sign(privateKey, digest); | bytes32 digest = keccak256(abi.encodePacked("\x19\x01",DOMAIN_SEPARATOR,getStructHash(message))); vm.sign(privateKey, digest); |
Use nonce to prevent Replay Attacks
A replay attack occurs when an attacker captures a valid signed message and resends it to execute the same action multiple times. This can be problematic, especially in cases like approving a token transfer.
To prevent this, you must use a nonce (number only once) in the message hash itself.
For example, let’s use the following Invoice struct again:
struct Invoice {
uint256 id;
address payer;
uint256 amountDue;
uint256 deadline; // Deadline timestamp, to be explained later
uint256 nonce;
}
You can create a mapping to store used nonce values for each payer. You should also have a view function that allows the signer to check if the nonce has already been used before including it in a message hash to be signed.
In your smart contract, you would then verify that the nonce from the message has not been used yet. If it has, the transaction must be reverted. This ensures that the action from the same signature cannot be executed twice.
Another option is to use OpenZeppelin’s Nonce.sol contract or look up Uniswap’s useUnorderedNonce implementation to save gas.
import {Nonces} from "@openzeppelin/contracts/utils/Nonces.sol";
function verifyInvoice(Invoice calldata invoice, bytes calldata signature) internal {
bytes32 structHash = keccak256(
abi.encode(
INVOICE_TYPEHASH,
invoice.id,
invoice.payer,
invoice.amountDue,
invoice.deadline,
_useNonce(invoice.payer)
)
);
// Rest of the logic goes here...
}
Deadline is a must
No matter whether you are using EIP-712 or not, when designing smart contracts that verify ECDSA signatures you must always enforce the usage of the deadline (expiration) timestamp for a signature. You don’t want User’s transaction with signature to execute after a year because it got stuck in the mempool, for example.
Instead, you should design a contract where the user must provide a deadline for a transaction with a signature to complete. Your contract will then compare that deadline with the block.timestamp.
If we again use the following Invoice struct as an example:
struct Invoice {
uint256 id;
address payer;
uint256 amountDue;
uint256 deadline;
uint256 nonce;
}
We must include a check for whether the deadline has expired or not.
import {Nonces} from "@openzeppelin/contracts/utils/Nonces.sol";
function verifyInvoice(Invoice calldata invoice, bytes calldata signature) internal {
bytes32 structHash = keccak256(
abi.encode(
INVOICE_TYPEHASH,
invoice.id,
invoice.payer,
invoice.amountDue,
invoice.deadline,
_useNonce(invoice.payer)
)
);
if (block.timestamp >= invoice.deadline) {
revert("Invoice expired");
}
bytes32 digest = hashTypedDataV4(structHash);
// function from the beginning of the article
verify(signature, digest);
}
Conclusion
In this article, we analyzed the best practices that should be followed when designing a smart contract that verifies ECDSA signatures. Here’s the cheat sheet that sums it up:
Replay attacks → Use nonce
Deadline is a must
Signature malleability → Do not use ecrecover precompile directly
→ If s is in the upper half, revert
Frontrunning → Verify against msg.sender or the claimed signer
Signature length → If it isn’t 65 (r, s, v) or 64 (r, vs), and not dealing with EIP-1271 signatures, revert
Same signature, different chain (Cross-chain replay attack) → Use EIP-191, EIP-712
Same signature, different dApp version → Use EIP-712
Same signature, invalid verifier contract → Use EIP-712
My name is Andrej and I hope you enjoyed reading this article. To receive the next one, subscribe to the Smart Contract Design Patterns newsletter. Thank you!
Subscribe to my newsletter
Read articles from Andrej directly inside your inbox. Subscribe to the newsletter, and don't miss out.
Written by
